Matrice idempotente

Sur cette page, nous expliquons ce que sont les matrices idempotentes. Nous vous montrons également plusieurs exemples de ce type de matrices afin que vous le compreniez parfaitement. Aussi, vous trouverez la formule pour trouver une matrice idempotente et, enfin, toutes les propriétés des matrices idempotentes.

Qu’est-ce qu’une matrice idempotente ?

La définition d’une matrice idempotente est la suivante :

Une matrice idempotente est cette matrice qui, multipliée par elle-même, donne la même matrice en conséquence.

$A\cdot A = A$

Par conséquent, toute puissance d’une matrice idempotente est égale à la matrice elle-même, quel que soit l’exposant :

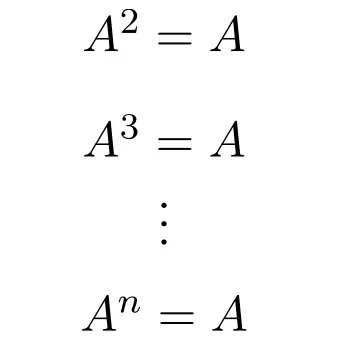
En fait, c’est la raison pour laquelle ce type de tableau tire son nom. Car en mathématiques, l’idempotence est une opération qui signifie qu’on obtient toujours le même résultat quel que soit le nombre de fois qu’elle est effectuée.

Exemples de matrices idempotentes

Une fois que nous connaissons le concept de matrice idempotente, nous allons voir quelques exemples de différentes dimensions pour finir de le comprendre.

Exemple de matrice idempotente 2×2

La matrice carrée suivante de dimension 2×2 est idempotente :

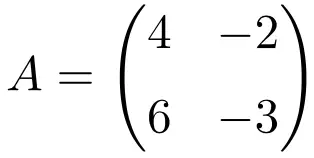
exemple de matrice idempotente de dimension 2x2

Pour vérifier qu’il s’agit d’une matrice idempotente, on calcule son carré :

$\displaystyle A^2=\begin{pmatrix} 4 &-2 \\[1.1ex] 6 & -3 \end{pmatrix}$

Le résultat est identique, on montre donc qu’il s’agit d’une matrice idempotente.

Exemple de matrice idempotente 3×3

La matrice carrée suivante de taille 3×3 est idempotente :

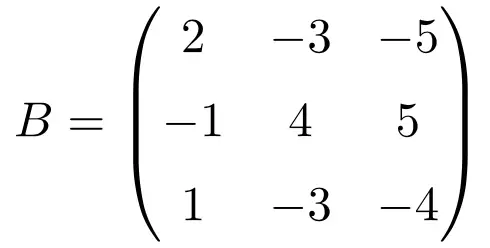
exemple de matrice idempotente de dimension 3x3

Pour vérifier qu’une matrice idempotente correspond bien, on élève la matrice à 2 :

$\displaystyle B^2=\begin{pmatrix} 2 &-3 & -5 \\[1.1ex] -1 & 4 & 5 \\[1.1ex] 1 & -3 & -4 \end{pmatrix}$

Le résultat est le même que la matrice d’origine, donc l’idempotence de la matrice est prouvée.

Structure d’une matrice idempotente 2×2

Ici, nous vous montrons la formule pour obtenir une matrice idempotente. Au cas où vous seriez plus intéressé, vous pouvez voir la démonstration de la formule ci-dessous dans les commentaires, mais c’est un peu fastidieux donc ici on vous laisse directement avec la formule des matrices idempotentes :

De telle manière que les éléments de la diagonale secondaire d’une matrice idempotente peuvent être quelconques tant que la condition est remplie

$a^2+bc=a$ et les nombres sur la diagonale principale doivent être $a$ et $1-a.$

En plus de toutes les matrices décrites par cette formule, il faut ajouter la matrice Identité, qui est également une matrice idempotente bien qu’elle ne respecte pas la formule. Si vous ne savez pas ce qu’est le tableau, vous pouvez demander ce qu’est le tableau Identity .

Propriétés des matrices idempotentes

Les matrices idempotentes ont les caractéristiques suivantes :

Le déterminant d’une matrice idempotente vaut toujours 0 ou 1.

À l’exception de la matrice d’identité, toutes les autres matrices idempotentes sont à la fois des matrices singulières ou dégénérées, c’est-à-dire qu’elles ne sont pas inversibles.

Toute matrice idempotente est diagonalisable, et ses valeurs propres (ou valeurs propres) sont toujours 0 ou 1.

La trace d’une matrice idempotente est égale au rang de la matrice.

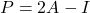Enfin, il existe une relation entre les matrices idempotentes et les matrices involutives : la matrice $A$ est idempotent si et seulement si la matrice $\displaystyle P= 2A-I$ c’est involutif.