Pada halaman ini kami menjelaskan apa itu vektor bebas linier dan vektor bergantung linier. Anda juga akan melihat contoh cara mengetahui apakah suatu himpunan vektor bergantung linier atau bebas. Dan, sebagai tambahan, Anda akan menemukan latihan dan memecahkan masalah langkah demi langkah tentang kemandirian dan ketergantungan linier.
Apa yang dimaksud dengan vektor bebas linier?
Himpunan vektor-vektor bebas dikatakan bebas linier jika tidak ada satupun vektor bebas yang dapat dituliskan sebagai kombinasi linier dari vektor-vektor bebas lainnya.
Dengan kata lain, diberikan himpunan vektor
![]()
Ini adalah independen linier jika satu-satunya solusi untuk persamaan berikut:
![]()
Ini semua adalah koefisiennya
![]()
sama dengan 0:
![]()
Secara geometris, dua vektor dikatakan bebas linier jika arahnya tidak sama, yaitu jika keduanya tidak sejajar.
Untuk singkatnya, terkadang kita mengatakan secara langsung bahwa mereka adalah vektor LI. Atau vektor-vektor tersebut mempunyai independensi linear.
Apa yang dimaksud dengan vektor bergantung linier?
Jelasnya, vektor bergantung linier berarti kebalikan dari vektor bebas linier. Oleh karena itu definisinya adalah:
Himpunan vektor-vektor bebas pada suatu bidang bergantung linier jika salah satu vektor tersebut dapat dinyatakan sebagai kombinasi linier dari vektor-vektor lain yang membentuk sistem.
Dengan kata lain, diberikan himpunan vektor
![]()
Ini bergantung linier jika terdapat solusi untuk persamaan berikut:
![]()
yang mempunyai koefisien tertentu
![]()
berbeda dari 0:
![]()
Hal sebaliknya juga berlaku: jika suatu vektor merupakan kombinasi linier dari vektor-vektor lain, maka semua vektor dalam himpunan bergantung linier.
Selain itu, jika dua vektor sejajar, berarti keduanya bergantung linier.
Kadang-kadang mereka juga disingkat dan disebut vektor LD. Atau bahkan vektor-vektor tersebut memiliki ketergantungan linier.
Contoh cara mengetahui vektor bergantung linier atau bebas
Kita kemudian akan melihat contoh khas vektor bergantung linier dan vektor bebas.
- Tentukan apakah 3 vektor 3 dimensi berikut mempunyai ketergantungan atau kemandirian linier:
![]()
![]()
![]()
Pertama, kita perlu menyatakan kondisi kombinasi linier:
![]()
Sekarang kita ganti setiap vektor dengan koordinatnya. Seperti nol, yang sesuai dengan vektor nol:
![]()
Koefisien dikalikan dengan vektor, sehingga ekspresi berikut ini ekuivalen:
![]()
Kami menambahkan vektor:
![]()
Jika kita perhatikan lebih dekat, persamaan sebelumnya berhubungan dengan 3 persamaan, karena setiap koordinat vektor kiri harus sama dengan setiap koordinat vektor kanan. Oleh karena itu kami memiliki sistem homogen yang terdiri dari 3 persamaan dengan 3 persamaan yang tidak diketahui:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1-2a_2+4a_3 = 0 \\[2ex] 5a_1+3a_2+2a_3 =0\\[2ex] 2a_1-a_2+a_3 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c6bb8117dd8ae715314efe73fe65eed8_l3.png)
Jadi satu-satunya hal yang perlu kita lakukan adalah menyelesaikan sistem persamaan yang tidak diketahui
![]()
Dan
![]()
Untuk melakukan ini, Anda dapat menggunakan metode apa pun (metode substitusi, metode Gaus, aturan Cramer, dll.). Akan tetapi, untuk mengetahui apakah vektor-vektornya LI atau LD, cukup dengan menentukan apakah terdapat solusi selain solusi sepele (semua koefisien sama dengan nol). JADI:
- Jika determinan matriks yang terdiri dari komponen-komponen vektor berbeda dari nol, berarti sistem persamaan tersebut hanya mempunyai satu solusi (
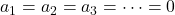
) dan, oleh karena itu, vektor-vektornya bebas linier
- Sebaliknya, jika determinan matriks yang terdiri dari komponen-komponen vektor sama dengan nol, hal ini berarti sistem persamaan mempunyai lebih dari satu penyelesaian dan oleh karena itu, vektor-vektor tersebut bergantung linier .
Jadi yang perlu dihitung hanyalah determinan dengan koordinat vektornya (karena determinan 3×3 maka dapat diselesaikan dengan aturan Sarrus). Penentu ini sesuai dengan koefisien sistem persamaan sebelumnya:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1&-2&4\\[1.1ex] 5&3&2 \\[1.1ex] 2&-1&1 \end{vmatrix} = -37 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-046e05ff603822985510c7bdc8b73021_l3.png)
Dalam hal ini determinannya berbeda dengan 0, sehingga vektor-vektornya bebas linier .
Oleh karena itu, satu-satunya solusi yang mungkin untuk sistem persamaan ini adalah solusi sepele dengan semua yang tidak diketahui sama dengan nol:
![]()
Sifat-sifat vektor bergantung linier dan bebas
Ketergantungan linier atau independensi suatu vektor mempunyai ciri-ciri sebagai berikut:
- Dua vektor proporsional sejajar dan oleh karena itu bergantung linier karena mempunyai arah yang sama.
- Demikian pula, jika dua vektor tidak mempunyai arah yang sama atau tidak sebanding, maka keduanya bebas linier.
- Tiga vektor koplanar (yang berada pada bidang yang sama) bebas linier.
- Vektor nol
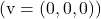
bergantung linier pada vektor apa pun.
- Himpunan vektor bebas linier menghasilkan ruang vektor dan membentuk basis vektor. Jika ketiga vektor tersebut tegak lurus maka merupakan basis ortogonal. Dan jika modulnya juga sama dengan 1, ini sesuai dengan basis ortonormal.
Menyelesaikan latihan ketergantungan dan kemandirian linier
Di bawah ini Anda memiliki beberapa latihan yang diselesaikan tentang vektor bergantung linier dan vektor bebas untuk dipraktikkan.
Latihan 1
Tentukan apakah vektor-vektor berikut bergantung linier atau bebas:
![]()
![]()
![]()
Kami pertama-tama mengajukan kondisi kombinasi linier:
![]()
![]()
![]()
![]()
Persamaan sebelumnya sesuai dengan sistem persamaan linear berikut:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1+2a_2+5a_3 = 0 \\[2ex] -2a_1+a_2-a_3 =0\\[2ex] a_1+3a_2+a_3 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-58f1b449f48096570437df0ca40f8a8d_l3.png)
Setelah kita menyatakan sistem persamaannya, kita menyelesaikan determinan matriks dengan suku-sukunya:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1&2&5\\[1.1ex] -2&1&-1 \\[1.1ex] 1&3&1 \end{vmatrix} = -29 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-caa6d4f135e79bb8b6d2368ff7eebefb_l3.png)
Dalam hal ini determinannya berbeda dengan 0, sehingga ketiga vektor tersebut bebas linier satu sama lain.
Latihan 2
Klasifikasikan vektor-vektor berikut sebagai bergantung linier atau bebas:
![]()
![]()
![]()
Pertama-tama kita ajukan persamaan kombinasi liniernya:
![]()
![]()
![]()
![]()
Dari persamaan sebelumnya diperoleh sistem persamaan homogen berikut:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1-2a_2+3a_3= 0 \\[2ex] 4a_1-a_3 =0\\[2ex] 3a_1+2a_2-4a_3 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c94610b6f8baef34a1fb4601c148f515_l3.png)
Setelah kita menyatakan sistem persamaannya, kita menyelesaikan determinan matriks dengan koordinat vektornya:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1&-2&3\\[1.1ex] 4&0&-1 \\[1.1ex] 3&2&-4 \end{vmatrix} \bm{= 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-67678c37fdaf0955ef8bbab8d34379f8_l3.png)
Dalam hal ini determinannya ekuivalen dengan 0, sehingga ketiga vektor bergantung secara linear satu sama lain.
Latihan 3
Untuk tiga vektor berikut, tunjukkan pasangan vektor mana yang bergantung linier dan pasangan vektor mana yang bebas linier.
![]()
Cara termudah untuk mengetahui apakah suatu pasangan vektor bergantung linier atau independen adalah dengan memeriksa apakah keduanya proporsional.
Kita cek dulu vektornya
![]()
dengan vektornya
![]()
![]()
Kedua, kita periksa vektornya
![]()
dengan vektornya
![]()
![]()
Terakhir, kami menguji vektornya
![]()
dengan vektornya
![]()
![]()
Jadi, satu-satunya pasangan vektor yang bergantung secara linier satu sama lain adalah
![]()
Dan
![]()
Selanjutnya hubungan mereka adalah sebagai berikut:
![]()
Atau setara:
![]()
Sebaliknya, pasangan vektor lainnya bebas linier.
Latihan 4
Pelajari ketergantungan linier atau independensi 4 vektor berikut satu sama lain:
![]()
![]()
![]()
![]()
Kami pertama-tama mengajukan kondisi kombinasi linier:
![]()
![]()
![]()
![]()
Dalam hal ini kita mempunyai sistem 3 persamaan dengan 4 persamaan yang tidak diketahui:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} -a_2+4a_3-2a_4 = 0 \\[2ex] a_1-2a_2+a_3-3a_4 =0\\[2ex] 2a_1-a_3+2a_4 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e9451263e5a31994569292e32666d93e_l3.png)
Kita tidak dapat menyelesaikan determinan seluruh matriks sistem, karena hanya matriks persegi yang dapat ditentukan. Oleh karena itu kita harus menghitung semua kemungkinan kombinasi determinan 3×3 dan melihat apakah salah satunya sama dengan 0, dalam hal ini vektor-vektornya akan bergantung linier, sebaliknya, jika semua determinan berbeda dari 0 maka 4 vektornya akan menjadi independen linier.
Kami menghitung determinan koefisien
![]()
Dan
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 0&-1&4\\[1.1ex] 1&-2&1 \\[1.1ex] 2&0&-1 \end{vmatrix} =13\bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-488d7848a40aa9a91bd5b3aa1f09b774_l3.png)
Penentu 3 koefisien pertama (atau 3 vektor pertama) berbeda dari nol. Jadi sekarang kita coba dengan determinan koefisiennya
![]()
Dan
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 0&-1&-2\\[1.1ex] 1&-2&-3 \\[1.1ex] 2&0&2 \end{vmatrix} \bm{= 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d1475a77f10ea0c16147a6f9c3f611b4_l3.png)
Kita memperoleh determinan nol, sehingga tidak perlu menghitung determinan lainnya karena kita sudah mengetahui bahwa keempat vektor tersebut bergantung linier .
Latihan 5
Hitung nilai dari
![]()
sehingga vektor-vektor berikut bebas linier:
![]()
![]()
![]()
Pertama-tama kita ajukan persamaan kombinasi liniernya:
![]()
![]()
![]()
![]()
Dari persamaan vektor sebelumnya diperoleh sistem persamaan homogen sebagai berikut:
![Rendered by QuickLaTeX.com \left. \begin{array}{l}3a_1-2a_2+a_3= 0 \\[2ex] -a_1+4a_2+3a_3 =0\\[2ex] 5a_1+7a_2+ka_3 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-16f88cbf406c1faf61307b99179a5de6_l3.png)
Setelah kita menyatakan sistem persamaannya, mari kita coba menyelesaikan determinan sistem tersebut:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3&-2&1\\[1.1ex] -1&4&3 \\[1.1ex] 5&7&k \end{vmatrix} =10k-120](https://mathority.org/wp-content/ql-cache/quicklatex.com-d748080bb1cacc1c80a35ef633a2d85e_l3.png)
Pernyataan tersebut memberitahu kita bahwa vektor-vektor harus bergantung linier. Oleh karena itu determinannya harus sama dengan nol:
![]()
![]()
![]()
![]()
Oleh karena itu, konstanta harus sama dengan 12 agar vektor-vektornya mempunyai ketergantungan linier.