Di sini Anda akan menemukan cara menurunkan sinus hiperbolik (rumus). Selain itu, Anda akan melihat beberapa contoh penyelesaian turunan sinus hiperbolik. Dan terakhir, kita buktikan rumus turunan fungsi trigonometri jenis ini.
Rumus yang berasal dari sinus hiperbolik
Turunan dari sinus hiperbolik x adalah kosinus hiperbolik dari x.
![]()
Oleh karena itu, turunan sinus hiperbolik suatu fungsi sama dengan hasil kali kosinus hiperbolik fungsi tersebut dan turunan fungsi tersebut.
![]()
Sebenarnya kedua rumus di atas sama, yang membedakan hanyalah pada rumus kedua kita menerapkan aturan rantai. Dan karena turunan x adalah 1, maka fungsinya tidak berubah.
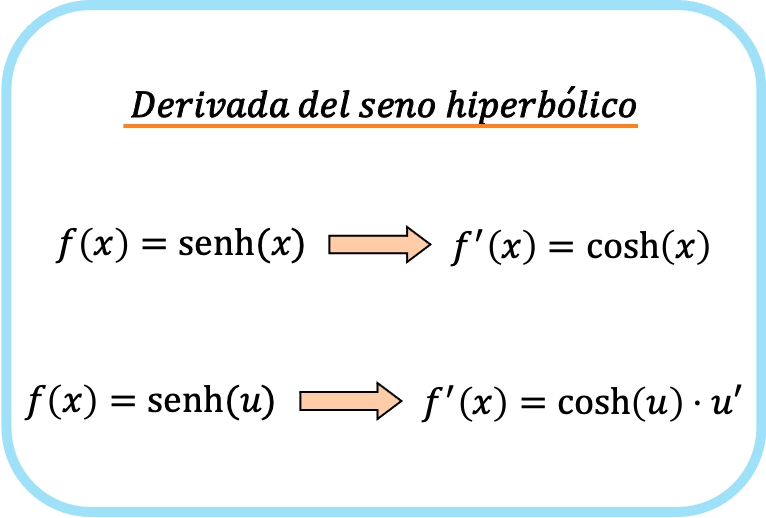
Seperti yang Anda lihat, rumus turunan sinus hiperbolik sangat mirip dengan rumus turunan sinus .
Contoh turunan sinus hiperbolik
Setelah kita mengetahui apa itu rumus turunan sinus hiperbolik, sekarang kita lanjutkan menyelesaikan beberapa contoh turunan sinus hiperbolik. Jadi, tentunya Anda sudah tidak ragu lagi bagaimana cara melakukannya.
Contoh 1: Turunan dari sinus hiperbolik 2x
![]()
Dalam hal ini, pada argumen sinus hiperbolik, kita memiliki fungsi yang berbeda dengan x, oleh karena itu, kita harus menggunakan rumus turunan sinus hiperbolik dengan aturan rantai untuk mencari turunannya:
![]()
Turunan dari 2x adalah 2, jadi turunan sinus hiperbolik dari 2x adalah kosinus hiperbolik dari 2x dikalikan 2.
![]()
Contoh 2: Turunan dari sinus hiperbolik x kuadrat
![]()
Rumus turunan fungsi sinus hiperbolik adalah:
![]()
Sebaliknya, turunan fungsi kuadrat x 2 adalah 2x. Oleh karena itu, turunan dari seluruh fungsi adalah:
![]()
Bukti rumus turunan sinus hiperbolik
Terakhir, kami akan mendemonstrasikan rumus turunan sinus hiperbolik. Untuk melakukan ini, kita akan mulai dari definisi matematis sinus hiperbolik:
![]()
Kami sekarang menyimpulkan dua sisi persamaan:
![]()
Untuk menurunkan ruas kanan persamaan, kita akan menggunakan rumus turunan pembagian:
![]()
➤ Lihat: turunan fungsi eksponensial dengan basis e
Dan tepatnya kita telah sampai pada ungkapan yang mendefinisikan kosinus hiperbolik. Sehingga turunan sinus hiperbolik terbukti :
![]()