Pada artikel ini kami menjelaskan cara menurunkan arcsinus suatu fungsi. Anda akan menemukan contoh turunan fungsi arcsinus dan Anda bahkan dapat berlatih dengan latihan yang diselesaikan langkah demi langkah. Terakhir, Anda juga akan melihat demonstrasi rumus turunan arcsinus.
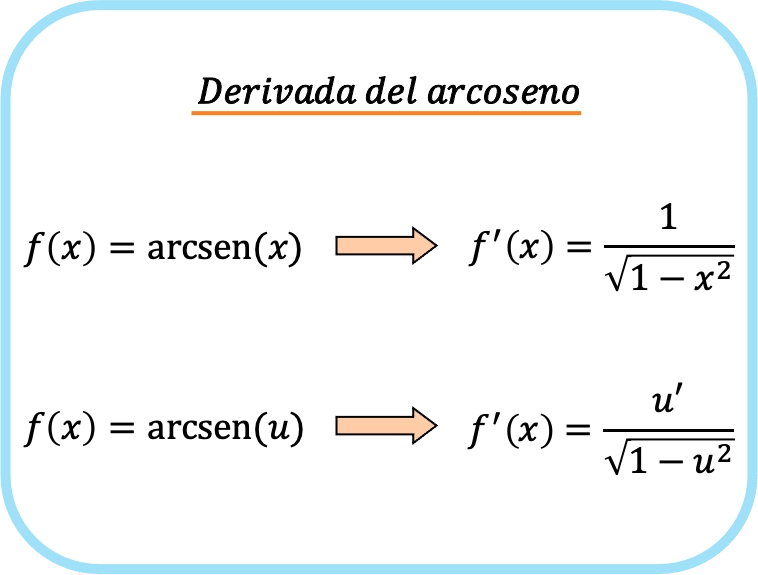
Apa turunan dari arcsinus?
Turunan arcsinus dari x adalah satu per akar kuadrat dari satu dikurangi x kuadrat.
![]()
Oleh karena itu, turunan arcsinus suatu fungsi sama dengan hasil bagi turunan fungsi tersebut dibagi dengan akar kuadrat satu dikurangi fungsi kuadrat.
![]()
Logikanya, rumus kedua diperoleh dengan menerapkan aturan rantai pada rumus pertama.
Ingatlah bahwa arcsinus adalah fungsi invers dari sinus, oleh karena itu disebut juga sinus invers.
Contoh turunan arcsinus
Setelah melihat apa rumus turunan arcsinus, kami akan menjelaskan beberapa contoh turunan trigonometri jenis ini. Dengan cara ini akan lebih mudah bagi Anda untuk memahami bagaimana arcsinus suatu fungsi diturunkan.
Contoh 1: Turunan dari arcsinus 2x
![]()
Untuk mencari turunan fungsi arcsinus, kita perlu menggunakan rumus yang sesuai:
![]()
Jadi turunan dari 2x adalah 2, jadi turunan arcsinus dari 2x adalah 2 dibagi akar satu dikurangi 2x kuadrat:
![]()
Contoh 2: Turunan dari arcsinus x kuadrat
![]()
Kami menggunakan rumus turunan arcsinus untuk menurunkannya:
![]()
Fungsi x 2 derajat dua, jadi turunannya adalah 2x. Jadi, turunan arcsinus x yang dipangkatkan 2 adalah:
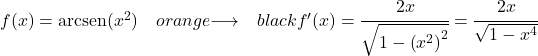
Contoh 3: Turunan dari arcsinus e x
![]()
Fungsi dalam contoh ini adalah fungsi komposit, jadi kita perlu menerapkan aturan rantai untuk menyelesaikan turunannya:
![]()
Turunan dari e x adalah dirinya sendiri, sehingga turunan seluruh fungsinya adalah:
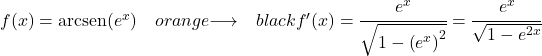
Masalah Terpecahkan Derivatif Arcsine
Turunkan fungsi arcsinus berikut:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
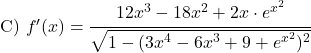
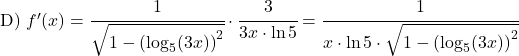
![Rendered by QuickLaTeX.com \begin{aligned}\text{E) } f'(x)& =\cfrac{1}{\sqrt{1-\left(\sqrt{4x}\right)^2}}\cdot \cfrac{4}{2\sqrt{4x}}\\[1.5ex] &=\cfrac{2}{\sqrt{1-4x}\cdot 2\sqrt{x}}\\[1.5ex] &=\cfrac{1}{\sqrt{x-4x^2}} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0a82c0fd18a8672100ed3b79525a1028_l3.png)
Bukti rumus turunan arcsinus
Selanjutnya kita lanjutkan ke pembuktian matematis rumus turunan arcsinus.
![]()
Pertama, kita ubah arcsinus menjadi sinus:
![]()
Sekarang kita bedakan kedua ruas persamaan:
![]()
Kami membersihkan Anda:
![]()
Selanjutnya, kita menerapkan identitas trigonometri dasar:
![]()
![]()
Dan, seperti yang kita simpulkan di atas bahwa x setara dengan sinus y, persamaannya tetap:
![]()
Seperti yang Anda lihat, dengan menerapkan prosedur ini kita memperoleh rumus turunan dari fungsi arcsinus, sehingga terlihat bahwa rumus tersebut terpenuhi.