Pada artikel ini kami menjelaskan cara menurunkan arccosecan hiperbolik suatu fungsi. Anda juga akan menemukan contoh turunan dari arccosecant hiperbolik.
Rumus turunan busur kosekan hiperbolik
Turunan kosekan busur hiperbolik dari x sama dengan negatif 1 dibagi hasil kali x dengan akar satu ditambah x kuadrat.
![]()
Oleh karena itu, turunan kosekan busur hiperbolik suatu fungsi adalah dikurangi turunan fungsi tersebut dibagi hasil kali fungsi tersebut dengan akar satu ditambah fungsi kuadrat.
![]()
Secara ringkas rumus menghitung turunan fungsi arccosecant hiperbolik adalah:
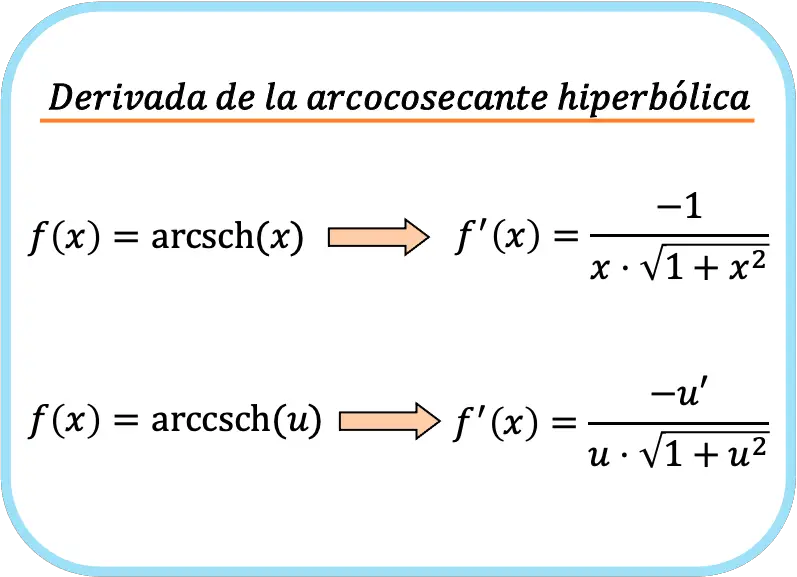
Meski kami telah memasukkan dua rumus, bukan berarti keduanya berbeda. Jika dicermati, rumus kedua sama seperti rumus pertama tetapi menerapkan aturan rantai.
Contoh turunan busur kosekan hiperbolik
Dengan mengetahui rumus turunan kosekan busur hiperbolik, kita kemudian akan menurunkan dua fungsi tersebut sehingga Anda dapat melihat cara kerjanya.
Contoh 1
![]()
Pada latihan kali ini kita harus menggunakan rumus turunan busur kosekan hiperbolik dengan aturan rantai, karena pada argumen tersebut terdapat fungsi selain x:
![]()
Jadi, untuk mencari turunannya, kita perlu mengganti u dengan 3x dan u’ dengan turunannya yaitu 3:
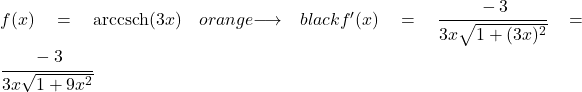
Contoh 2
![]()
Dalam hal ini kita mempunyai fungsi polinomial dalam argumen arccosecant hiperbolik, jadi kita juga perlu menggunakan aturan rantai untuk menurunkannya:
![]()
Jadi kita letakkan turunan dari fungsi argumen di pembilang pecahan, dan di penyebutnya kita ubah u dengan fungsi polinomial:
![Rendered by QuickLaTeX.com \begin{aligned}f(x)=\text{arccsch}(x^5-2x^3) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}f'(x)&=\cfrac{-(5x^4-6x^2)}{(x^5-2x^3)\sqrt{1+(x^5-2x^3)^2}}\\[1.5ex] &=\cfrac{-5x^4+6x^2}{(x^5-2x^3)\sqrt{1+(x^5-2x^3)^2}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6257584425bd348ba75c7680d8ff6f70_l3.png)