▷ Turunan suatu produk (rumus dan latihan yang diselesaikan)

Pada artikel ini kami menjelaskan cara menurunkan hasil kali dua fungsi (rumus). Selain itu, Anda juga dapat melihat beberapa contoh turunan perkalian fungsi dan bahkan berlatih menyelesaikan soal turunan perkalian.

Rumus turunan suatu produk

Turunan suatu hasil kali dua fungsi yang berbeda sama dengan hasil kali turunan fungsi pertama dengan fungsi kedua yang tidak terdiferensiasi ditambah hasil kali fungsi pertama yang tidak terdiferensiasi dengan turunan fungsi kedua.

Dengan kata lain, jika f(x) dan g(x) merupakan dua fungsi yang berbeda, maka rumus turunan perkalian kedua fungsi tersebut adalah sebagai berikut:

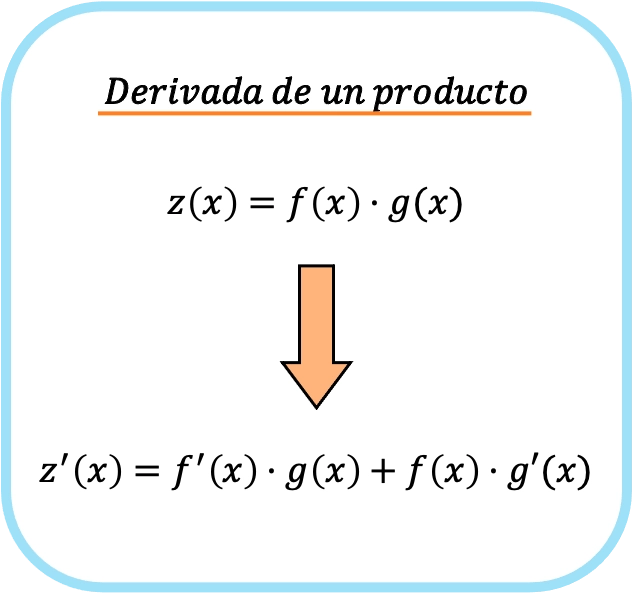
Jadi, dengan menerapkan aturan turunan suatu produk, kita beralih dari perkalian sederhana ke dua produk berbeda.

Contoh turunan suatu produk

Setelah kita mengetahui rumus turunan suatu hasil kali (atau perkalian), kita akan menyelesaikan beberapa contoh turunan jenis ini. Ini akan memudahkan Anda memahami bagaimana hasil kali dua fungsi diturunkan.

Contoh 1

Dalam contoh ini kita akan menyelesaikan turunan dua fungsi potensial dengan mengalikan:

$f(x)=5x^2\cdot (x^3+4x-6)$

Seperti yang kita lihat pada bagian sebelumnya, rumus turunan perkalian adalah:

$\begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}$

Oleh karena itu, pertama-tama kita harus menghitung turunan masing-masing fungsi secara terpisah:

$\cfrac{d}{dx}\ 5x^2=10x$

$\cfrac{d}{dx}\ (x^3+4x-6)=3x^2+4$

Dan setelah kita mengetahui turunan setiap fungsi, kita bisa menerapkan rumus turunan hasil kali dua fungsi. Artinya, kita mengalikan turunan faktor pertama dengan faktor kedua tanpa membedakan, lalu menjumlahkan hasil kali faktor pertama tanpa membedakan dengan turunan faktor kedua:

$\begin{array}{c}f(x)=5x^2\cdot (x^3+4x-6)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=10x\cdot (x^3+4x-6)+5x^2\cdot (3x^2+4)\end{array}$

Terakhir, kami melakukan operasi untuk menyederhanakan hasil yang diperoleh:

$\begin{aligned}f'(x)& =10x\cdot (x^3+4x-6)+5x^2\cdot (3x^2+4)\\[1.5ex] & = 10x^4+40x^2-60x +15x^4+20x^2 \\[1.5ex] & = 25x^4+60x^2-60x\end{aligned}$

Contoh 2

Dalam hal ini kita akan menurunkan hasil kali konstanta dengan suatu fungsi:

$f(x)=7\cdot (x^2+3x)$

Aturan turunan suatu produk adalah sebagai berikut:

$\begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}$

Jadi, kami secara terpisah menurunkan setiap fungsi yang merupakan bagian dari produk:

$\cfrac{d}{dx}\ 7=0$

$\cfrac{d}{dx}\ (x^2+3x)=2x+3$

Lalu kita terapkan aturan turunan perkalian:

$\begin{array}{c}f(x)=7\cdot (x^2+3x)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=0\cdot (x^2+3x)+7\cdot (2x+3)=14x+21\end{array}$

Perhatikan bahwa turunan suatu konstanta selalu nol, sehingga kita dapat menyimpulkan bahwa turunan dari perkalian suatu konstanta dengan suatu fungsi sama dengan hasil kali konstanta dan turunan fungsi tersebut.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}z(x)=k\cdot f(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=k\cdot f'(x)\end{array} \end{empheq}$

Contoh 3

Mari kita selesaikan hasil kali antara fungsi eksponensial dan logaritma natural:

$f(x)=4^{3x}\cdot \ln(x^2)$

Rumus turunan perkalian dua fungsi adalah:

$\begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}$

Oleh karena itu kita harus terlebih dahulu membuat turunan masing-masing fungsi yang membentuk hasil perkaliannya secara terpisah, yaitu sebagai berikut:

$\cfrac{d}{dx}\ 4^{3x}=4^{3x}\cdot \ln (4) \cdot 3$

$\cfrac{d}{dx}\ \ln(x^2)=\cfrac{2x}{x^2}=\cfrac{2}{x}$

Oleh karena itu, hasil kali turunan dari fungsi-fungsi tersebut adalah:

$\begin{array}{c}f(x)=4^{3x}\cdot \ln(x^2)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=4^{3x}\cdot \ln (4) \cdot 3\cdot \ln(x^2) +4^{3x}\cdot \cfrac{2}{x} \end{array}$

Latihan soal turunan suatu produk

Turunkan produk fungsi berikut:

$\text{A) }f(x)=5\ln(3x)$

$\text{B) }f(x)=(4x^2+1)(6x^3-7)$

$\text{C) }f(x)=\text{cos}(4x)\cdot e^{x^2}$

$\text{D) }f(x)=(3x^3-4x^2+8x)\cdot \sqrt{6x^2+3x}$

$\text{E) }f(x)=5^{4x}\cdot \log_9(x^3-x)$

$\text{F) }f(x)=\left(10x^6-6x^5\right)^4\cdot \text{arcsen}(x^2+9x)$

Lihat solusinya

$\text{A) } f'(x)=5\cdot \cfrac{3}{3x} =\cfrac{5}{x}$

$\begin{aligned}\text{B) }f'(x)&=8x\cdot (6x^3-7)+(4x^2+1)\cdot 18x^2\\[1.2ex]&=48x^4-56x+72x^4+18x^2\\[1.2ex]&=120x^4+18x^2-56x \end{aligned}$

$\text{C) }f'(x) =-4\text{sen}(4x)\cdot e^{x^2}+\text{cos}(4x)\cdot e^{x^2}\cdot 2x$

$\text{D) }f'(x)=(9x^2-8x+8)\cdot \sqrt{6x^2+3x}+(3x^3-4x^2+8x)\cdot\cfrac{12x+3}{2\sqrt{6x^2+3x}}$

$\text{E) }f'(x)=5^{4x}\cdot \ln(5) \cdot 4 \cdot \log_9(x^3-x)+ 5^{4x}\cdot\cfrac{3x^2-1}{(x^3-x)\ln(9)}$

$\begin{aligned}\text{F) }f'(x)=& 4\left(10x^6-6x^5\right)^3\cdot (60x^5-30x^4)\cdot \text{arcsen}(x^2+9x)\ +\\[1.2ex] &+\left(10x^6-6x^5\right)^4\cdot \cfrac{2x+9}{\sqrt{1-\left(x^2+9x\right)^2}}\end{aligned}$

Berasal dari produk tiga fungsi

Selanjutnya, kami tinggalkan rumus turunan dari perkalian 3 fungsi, karena rumus ini sangat mirip dengan rumus 2 fungsi dan dapat berguna dalam beberapa kasus.

Turunan suatu hasil kali tiga fungsi sama dengan hasil kali turunan fungsi pertama dan dua fungsi lainnya, ditambah hasil kali turunan fungsi kedua dan dua fungsi lainnya, ditambah hasil kali turunan fungsi tersebut. fungsi ketiga.fungsi dengan dua fungsi lainnya.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=1mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}z(x)=f(x)\cdot g(x)\cdot h(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)\cdot h(x)+f(x)\cdot g'(x)\cdot h(x)+f(x)\cdot g(x)\cdot h'(x)\end{array} \end{empheq}$

Misalnya, jika kita ingin menurunkan perkalian tiga fungsi berbeda berikut ini:

$f(x)=3x\cdot e^{2x} \cdot \text{sen}(x)$

Untuk menyelesaikan turunan, kita harus menerapkan aturan turunan dari hasil kali tiga fungsi, oleh karena itu:

$f'(x)=3\cdot e^{2x} \cdot \text{sen}(x)+3x\cdot 2e^{2x} \cdot \text{sen}(x)+3x\cdot e^{2x} \cdot \text{cos}(x)$

Demonstrasi rumus turunan suatu produk

Terakhir, kami akan mendemonstrasikan rumus turunan perkalian. Anda tidak harus menghafalnya, tetapi ada baiknya untuk selalu memahami dari mana rumusnya berasal. 🙂

Dari definisi matematis turunan:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Misalkan fungsi z merupakan hasil kali dua fungsi yang berbeda:

$z(x)=f(x)\cdot g(x)$

Maka turunan dari z menurut definisinya adalah:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{\bigl[f(x+h)\cdot g(x+h)\bigr]-\bigl[f(x)\cdot g(x)\bigr]}{h}$

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x+h)-f(x)\cdot g(x)}{h}$

Seperti yang kita ketahui, jika kita menjumlahkan suatu suku dengan cara penjumlahan dan pengurangan, maka tidak akan mempengaruhi hasilnya selama keduanya merupakan suku yang sama. Oleh karena itu, kita dapat melanjutkan ke langkah berikutnya:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x+h)\color{orange}\bm{-f(x+h)\cdot g(x)+f(x+h)\cdot g(x)}\color{black}-f(x)\cdot g(x)}{h}$

Kami sekarang menggunakan properti batas untuk memisahkan batas sebelumnya menjadi dua batas berbeda:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x+h)-f(x+h)\cdot g(x)}{h}+\lim_{h \to 0}\frac{f(x+h)\cdot g(x)-f(x)\cdot g(x)}{h}$

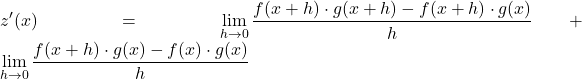
Kami mengekstrak faktor persekutuan dalam pembilang kedua pecahan:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\bigl(g(x+h)-g(x)\bigr)}{h}+\lim_{h \to 0}\frac{g(x)\bigl(f(x+h)-f(x)\bigr)}{h}$

Di sisi lain, kita mengetahui hasil dari limit berikut:

$\displaystyle \lim_{h \to 0}f(x+h)=f(x)$

Oleh karena itu, kita dapat menyederhanakan batasannya:

$\displaystyle z'(x)=\lim_{h \to 0}f(x+h)\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}+\lim_{h \to 0}g(x)\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

$\displaystyle z'(x)=f(x)\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}+g(x)\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Terakhir, dengan melihat dua limit yang tersisa, masing-masing sesuai dengan definisi turunan suatu fungsi. Oleh karena itu, kesetaraan dapat disederhanakan:

$\displaystyle z'(x)=f(x)\cdot g'(x)+g(x)\cdot f'(x)$

Atau setara:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x) \end{empheq}$

Turunan dari suatu produk (atau perkalian)

Rumus turunan suatu produk

Contoh turunan suatu produk

Contoh 1

Contoh 2

Contoh 3

Latihan soal turunan suatu produk

Berasal dari produk tiga fungsi

Demonstrasi rumus turunan suatu produk

Tinggalkan Komentar Batalkan Balasan