Turunan dari hasil bagi (pembagian): rumus dan latihan yang diselesaikan

Pada artikel ini kami menjelaskan cara menurunkan hasil bagi (atau pembagian) dari dua fungsi. Anda akan menemukan contoh turunan hasil bagi fungsi dan, sebagai tambahan, Anda akan dapat berlatih dengan latihan langkah demi langkah tentang turunan pembagian.

Rumus turunan suatu hasil bagi

Turunan suatu koefisien (atau pembagian) fungsi sama dengan turunan fungsi pembilang dengan penyebut fungsi yang lebih kecil dari fungsi pembilang dengan turunan fungsi penyebut dibagi kuadrat fungsi penyebut tinggi.

rumus turunan suatu pembagian atau hasil bagi

Seperti yang Anda lihat, ketika kita menerapkan aturan turunan dari hasil bagi (atau pembagian), kita masih memiliki pecahan setelah diferensiasi. Namun, selain itu, pada pembilangnya kita memiliki dua perkalian dan satu pengurangan, dan penyebutnya dipangkatkan dua.

Contoh turunan dari hasil bagi

Kita baru saja melihat apa rumus turunan hasil bagi dua fungsi, selanjutnya kita akan menyelesaikan beberapa contoh turunan dari operasi jenis ini. Ingat, jika Anda belum memahami cara menurunkan hasil bagi fungsional, Anda dapat bertanya kepada kami di bagian komentar.

Contoh 1

Dalam contoh ini, kita akan menurunkan fungsi potensial dibagi fungsi trigonometri:

$f(x)=\cfrac{3x^2+4x}{\text{sen}(2x)}$

Rumus turunan pembagian dua fungsi berbeda adalah sebagai berikut:

$\begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}$

Jadi pertama-tama kita perlu menghitung turunan masing-masing fungsi secara terpisah:

$\cfrac{d}{dx}\ (3x^2+4x)=6x+4$

$\cfrac{d}{dx}\ \text{sen}(2x)=2\text{cos}(2x)$

Oleh karena itu, turunan dari seluruh fungsi adalah:

$\begin{array}{c}f(x)=\cfrac{3x^2+4x}{\text{sen}(2x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{(6x+4)\cdot\text{sen}(2x)-(3x^2+4x)\cdot 2\text{cos}(2x)}{\text{sen}^2(2x)}\end{array}$

Contoh 2

Dalam hal ini kita akan mencari turunan suatu konstanta dibagi suatu fungsi:

$f(x)=\cfrac{10}{x^2+3x-9}$

Seperti yang kita lihat di atas, aturan turunan pembagian dua fungsi berbeda adalah sebagai berikut:

$\begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}$

Jadi, kita menghitung turunan pembilang dan penyebutnya secara terpisah:

$\cfrac{d}{dx}\ 10=0$

$\cfrac{d}{dx}\ (x^2+3x-9)=2x+3$

Dan terakhir, kita temukan turunan dari pembagian bilangan bulat:

$\begin{array}{c}f(x)=\cfrac{10}{x^2+3x-9}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{0\cdot (x^2+3x-9)-10\cdot (2x+3)}{\left(x^2+3x-9\right)^2}=\cfrac{-20x+30}{\left(x^2+3x-9\right)^2}\end{array}$

Faktanya, kita dapat memperoleh rumus untuk mendiferensiasikan secara langsung ketika kita memiliki konstanta pada pembilangnya dibagi suatu fungsi, karena turunan dari konstanta tersebut selalu 0. Oleh karena itu, rumus berikut akan selalu benar:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}z(x)=\cfrac{k}{f(x)} \\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{-k\cdot f'(x)}{\bigl(f(x)\bigr)^2}\end{array} \end{empheq}$

Contoh 3

Dalam latihan ini, kita akan memperoleh hasil bagi dua polinomial:

$f(x)=\cfrac{x^3+4x^2}{5x^2-8}$

Untuk menyelesaikan turunan, kita harus menerapkan aturan turunan dari hasil bagi dua fungsi yang berbeda, yaitu sebagai berikut:

$\begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}$

Sekarang mari kita cari turunan dari polinomial pembilang dan polinomial penyebutnya:

$\cfrac{d}{dx}\ (x^3+4x^2)=3x^2+8x$

$\cfrac{d}{dx}\ (5x^2-8)=10x$

Oleh karena itu, turunan dari pembagian polinonim adalah:

$\begin{array}{c}f(x)=\cfrac{x^3+4x^2}{5x^2-8}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\end{array}$

Dan terakhir, kami melakukan operasi dan menyederhanakan pecahan sebanyak mungkin:

$\begin{aligned}f'(x)&=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\\[2ex]&=\cfrac{15x^4-24x^2+40x^3-64x-10x^4-40x^3}{25x^4+64-80x^2}\\[2ex]&=\cfrac{5x^4-24x^2-64x}{25x^4-80x^2+64}\end{aligned}$

Latihan soal turunan dari suatu hasil bagi

Turunkan pembagian fungsi berikut:

$\text{A) }f(x)=\cfrac{9x^2+5x}{6x^3}$

$\text{B) }f(x)=\cfrac{19}{2x^2-2}$

$\text{C) }f(x)=\cfrac{8x^3-4x^2+3x}{e^{4x}}$

$\text{D) }f(x)=\cfrac{\text{cos}(x^2)}{\text{sen}(6x)}$

$\text{E) }f(x)=\cfrac{\ln(x^3+4)}{\left(4x^2-3x\right)^3}$

$\text{F) }f(x)=\cfrac{\sqrt{x^2+4x}}{5^{x^2}}$

Lihat solusinya

$\begin{aligned}\text{A) }f'(x)&=\cfrac{(18x+5)\cdot 6x^3-(9x^2+5x)\cdot 18x^2}{\left(6x^3\right)^2}\\[1.5ex]&=\cfrac{108x^4+30x^3-162x^4-90x^3}{36x^6}\\[1.5ex]&=\cfrac{-54x^4-60x^3}{36x^6}\\[1.5ex]&=\cfrac{-9x-10}{6x^3}\end{aligned}$

$\text{B) }f'(x)=\cfrac{-19\cdot 4x}{\left(2x^2-2\right)^2}=\cfrac{-76x}{\left(2x^2-2\right)^2}$

$\begin{aligned}\text{C) }f'(x)&=\cfrac{(24x^2-8x+3)e^{4x}-(8x^3-4x^2+3x)\cdot 4e^{4x}}{\left(e^{4x}\right)^2}\\[1.5ex]&=\cfrac{e^{4x}(24x^2-8x+3-32x^3+16x^2-12x)}{e^{8x}}\\[1.5ex]&=\cfrac{-32x^3+40x^2-20x+3}{e^{4x}}\end{aligned}$

$\text{D) }f'(x)=\cfrac{-2x\text{sen}(x^2)\cdot\text{sen}(6x)-\text{cos}(x^2)\text{cos}(6x)\cdot 6}{\text{sen}^2(6x)}$

$\begin{aligned}\text{E) }f'(x)&=\cfrac{\cfrac{3x^2}{x^3+4}\cdot\left(4x^2-3x\right)^3-\ln(x^3+4)\cdot 3\left(4x^2-3x\right)^2\cdot (8x-3) }{\left(\left(4x^2-3x\right)^3\right)^2}\\[1.5ex]&=\cfrac{\cfrac{3x^2}{x^3+4}\cdot\left(4x^2-3x\right)^3-\ln(x^3+4)\cdot 3\left(4x^2-3x\right)^2\cdot (8x-3) }{\left(4x^2-3x\right)^6}\end{aligned}$

$\begin{aligned}\text{F) }f'(x)&=\cfrac{\cfrac{2x+4}{2\sqrt{x^2+4x}}\cdot 5^{x^2} - \sqrt{x^2+4x}\cdot 5^{x^2}\cdot \ln(5) \cdot 2x }{\left(5^{x^2}\right)^2}\\[1.5ex]&=\cfrac{\cfrac{2x+4}{2\sqrt{x^2+4x}}\cdot 5^{x^2} - \sqrt{x^2+4x}\cdot 5^{x^2}\cdot \ln(5) \cdot 2x }{5^{2x^2}}\end{aligned}$

Demonstrasi turunan suatu hasil bagi

Terakhir, kami akan mendemonstrasikan rumus turunan suatu pembagian. Untuk melakukannya, kita akan menggunakan definisi umum dari turunan, yaitu:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Misalkan z merupakan pembagian dua fungsi yang berbeda:

$z(x)=\cfrac{f(x)}{g(x)}$

Maka, turunan fungsi z yang menerapkan definisi matematika adalah:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{\cfrac{f(x+h)}{g(x+h)}-\cfrac{f(x)}{g(x)}}{h}$

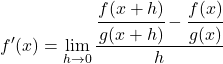
Kami menyelesaikan pengurangan pecahan dari pembilang pecahan:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{\cfrac{f(x+h)\cdot g(x)}{g(x+h)\cdot g(x)}-\cfrac{f(x)\cdot g(x+h)}{g(x)\cdot g(x+h)}}{h}$

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x)-f(x)\cdot g(x+h)}{h\cdot g(x)\cdot g(x+h)}$

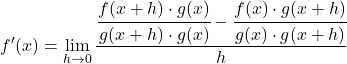
Menambah suku penjumlahan dan pengurangan pada suatu persamaan tidak mengubah persamaan tersebut. Oleh karena itu, kita dapat melanjutkan ke langkah berikutnya:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x)\color{orange}\bm{-f(x)\cdot g(x)}\color{black}-f(x)\cdot g(x+h)\color{orange}\bm{+f(x)\cdot g(x)}\color{black}}{h\cdot g(x)\cdot g(x+h)}$

Kami mengekstrak faktor persekutuan:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{g(x)\bigl[f(x+h)-f(x)\bigr]-f(x)\bigl[g(x+h)-g(x)\bigr]}{h\cdot g(x)\cdot g(x+h)}$

Sekarang mari kita pindahkan suku h dari penyebut ke pembilang menggunakan sifat-sifat pecahan:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{g(x)\cdot \cfrac{f(x+h)-f(x)\cdot g(x)}{h}-f(x)\cdot\cfrac{g(x+h)-g(x)}{h}}{g(x)\cdot g(x+h)}$

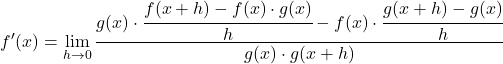
Kami mengubah persamaan dengan menerapkan sifat-sifat limit:

$\displaystyle f'(x)=\frac{g(x)\cdot \displaystyle\lim_{h \to 0}\cfrac{f(x+h)-f(x)\cdot g(x)}{h}-f(x)\cdot\lim_{h \to 0}\cfrac{g(x+h)-g(x)}{h}}{g(x)\cdot \displaystyle\lim_{h \to 0}g(x+h)}$

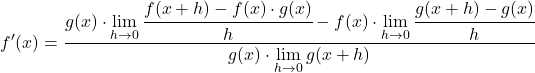
Batas pembilangnya sesuai dengan definisi matematis dari turunan setiap fungsi, oleh karena itu:

$\displaystyle f'(x)=\frac{g(x)\cdot f'(x)-f(x)\cdot g'(x)}{g(x)\cdot \displaystyle\lim_{h \to 0}g(x+h)}$

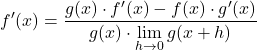
Selesaikan limit penyebut pecahan:

$\displaystyle f'(x)=\frac{g(x)\cdot f'(x)-f(x)\cdot g'(x)}{g(x)\cdot g(x)}$

Dan dengan demikian rumus turunan dari hasil bagi dua fungsi ditunjukkan:

$\displaystyle f'(x)=\frac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}$

Turunan dari hasil bagi (atau pembagian)

Rumus turunan suatu hasil bagi

Contoh turunan dari hasil bagi

Contoh 1

Contoh 2

Contoh 3

Latihan soal turunan dari suatu hasil bagi

Demonstrasi turunan suatu hasil bagi

Tinggalkan Komentar Batalkan Balasan