Di sini Anda akan menemukan turunan dari tangen hiperbolik suatu fungsi. Selain itu, Anda akan dapat melihat beberapa contoh penyelesaian turunan garis singgung hiperbolik. Dan terakhir, kami tunjukkan rumus turunan tangen hiperbolik.
Rumus turunan tangen hiperbolik
Turunan tangen hiperbolik x sama dengan 1 dibagi kuadrat kosinus hiperbolik x. Turunan garis singgung x juga setara dengan kuadrat garis potong hiperbolik x, dan 1 dikurangi kuadrat garis singgung hiperbolik x.
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{tanh}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cosh}^2(x)}=\text{sech}^2(x)=1-\text{tanh}^2(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9a7c392afdb3bbf504e167e15fb2fee6_l3.png)
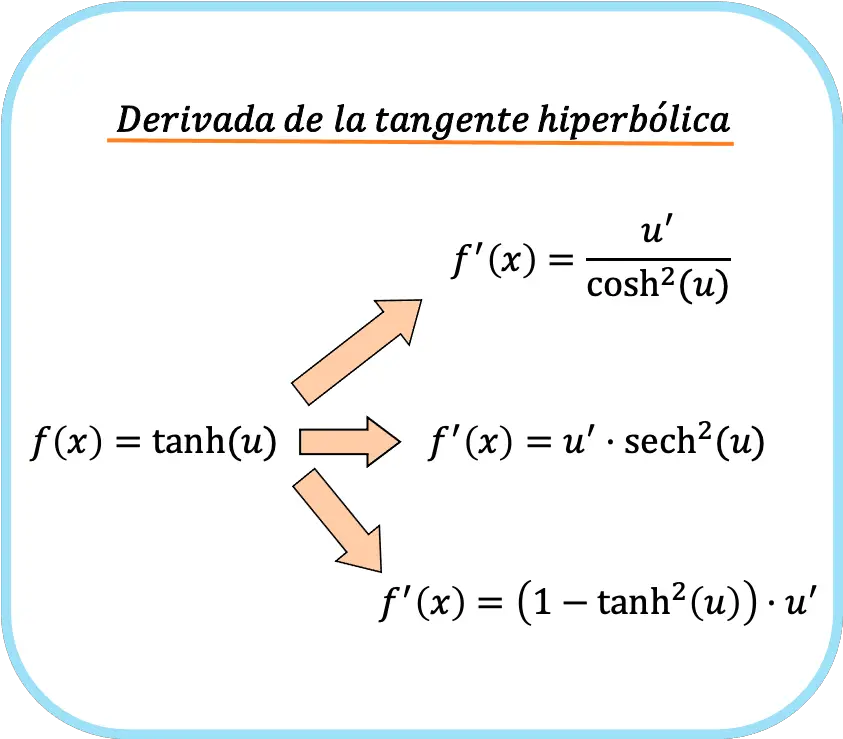
Sebaliknya, jika dalam argumen fungsi kita mempunyai fungsi selain x, kita harus menerapkan aturan rantai. Lalu ketiga rumus turunan tangen hiperbolik tersebut adalah:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{tanh}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cosh}^2(u)}=\text{sech}^2(u)\cdot u'=\left(1-\text{tanh}^2(u)\right)\cdot u'\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b5ee01c6675067b20f71ea8ac4efcfe5_l3.png)
Ini tidak berarti bahwa setiap kali kita menurunkan garis singgung hiperbolik kita harus menggunakan ketiga rumus tersebut, namun kita dapat menggunakan salah satu rumus tersebut untuk menurunkannya. Jadi, bergantung pada fungsi argumen tangen hiperbolik, akan lebih baik menggunakan satu rumus atau lainnya. Di bawah ini adalah beberapa contoh di mana Anda dapat melihat bagaimana tangen hiperbolik suatu fungsi diturunkan.
Turunan garis singgung hiperbolik hampir sama dengan turunan garis singgung, namun memiliki detail kecil yang membuatnya sangat berbeda. Anda bisa melihat perbedaannya pada link berikut:
➤ Lihat: rumus turunan tangen
Contoh turunan dari garis singgung hiperbolik
Setelah melihat apa rumus turunan tangen hiperbolik, berikut beberapa contoh penyelesaian turunan fungsi trigonometri jenis ini agar Anda paham betul cara menurunkan tangen hiperbolik.
Contoh 1: Turunan dari garis singgung hiperbolik 2x
![]()
Untuk mendapatkan tangen hiperbolik dalam contoh ini, kita akan menggunakan rumus kosinus hiperbolik, meskipun Anda tentu saja dapat menggunakan mana pun yang Anda suka.
![]()
Kita tahu bahwa turunan dari 2x adalah 2, jadi turunan seluruh fungsinya adalah:
![]()
Contoh 2: Turunan dari garis singgung hiperbolik x kuadrat
![]()
Aturan turunan tangen hiperbolik suatu fungsi adalah:
![]()
Di satu sisi, kita membedakan fungsi dari argumen x 2 , yang menghasilkan 2x, lalu kita menyelesaikan turunan seluruh fungsi menggunakan rumus:
![]()
Contoh 3: Turunan dari garis singgung hiperbolik pangkat tiga
![]()
Dalam hal ini, kita harus memperoleh tangen hiperbolik dari suatu fungsi yang, terlebih lagi, dipangkatkan. Jadi kita perlu menggunakan rumus turunan fungsi potensial, aturan turunan tangen hiperbolik, dan aturan rantai:
![]()
Bukti turunan garis singgung
Pada bagian ini, kita akan mendemonstrasikan rumus turunan tangen hiperbolik. Dan untuk itu, kita akan mulai dari identitas trigonometri yang menghubungkan ketiga perbandingan trigonometri hiperbolik:
![]()
➤ Catatan: Untuk memahami pembuktiannya, Anda perlu mengetahui apa turunan dari sinus hiperbolik dan apa turunan dari kosinus hiperbolik . Oleh karena itu, kami menyarankan Anda mengunjungi halaman tertaut sebelum melanjutkan.
Sekarang, mari kita terapkan rumus turunan hasil bagi:
![]()
![]()
![]()
Kami mengurangi ekspresi pembilang pecahan menggunakan rumus berikut:
![]()
![]()
Seperti yang Anda lihat, persamaan sebelumnya sesuai dengan rumus pertama untuk turunan tangen hiperbolik. Begitu pula dengan garis potong hiperbolik merupakan kebalikan perkalian dari kosinus hiperbolik, sehingga rumus kedua juga diturunkan:
![]()
Terakhir, kita dapat sampai pada aturan ketiga turunan tangen hiperbolik dengan mengubah pecahan dari langkah sebelumnya menjadi pengurangan pecahan:
![]()
![]()
![]()