Pada artikel ini kami menjelaskan cara menurunkan garis potong hiperbolik suatu fungsi. Anda akan menemukan rumus turunan garis potong hiperbolik dan beberapa contoh kerja turunan jenis ini.
Rumus turunan dari garis potong hiperbolik
Turunan garis potong hiperbolik x sama dengan dikurangi hasil kali garis potong hiperbolik x dikalikan garis singgung hiperbolik x.
![]()
Oleh karena itu, turunan garis potong hiperbolik suatu fungsi adalah dikurangi hasil kali garis potong hiperbolik fungsi tersebut dikali tangen hiperbolik fungsi tersebut dikalikan dengan turunan fungsi tersebut.
![]()
Singkatnya, rumus turunan fungsi garis potong hiperbolik adalah:
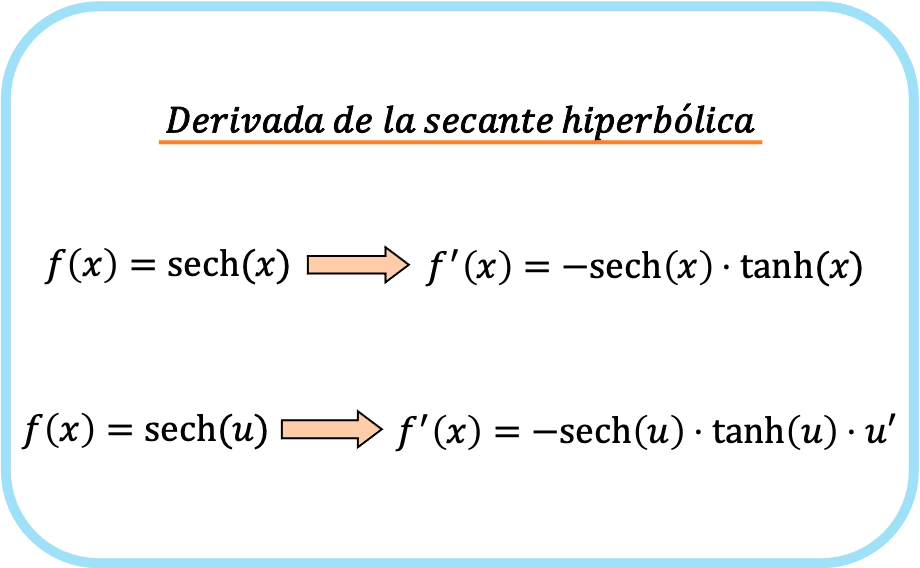
Perhatikan bahwa kedua ekspresi sebenarnya termasuk dalam satu rumus. Satu-satunya perbedaan adalah bahwa rumus kedua menerapkan aturan rantai.
Contoh turunan dari garis potong hiperbolik
Sekarang setelah kita mengetahui rumus turunan garis potong hiperbolik, kita akan melihat beberapa penyelesaian soal turunan trigonometri jenis ini.
Contoh 1
![]()
Dalam contoh ini kita mempunyai fungsi yang berbeda dengan x pada argumen garis potong hiperbolik, jadi untuk menurunkannya kita perlu menggunakan rumus aturan rantai.
![]()
Karena fungsi 2x linier, maka turunannya adalah 2. Oleh karena itu, untuk mencari turunannya, kita cukup mengganti u dengan 2x dan u’ dengan 2 dengan rumus:
![]()
Contoh 2
![]()
Fungsi latihan ini bersifat majemuk, karena garis potong hiperbolik mempunyai fungsi lain dalam argumennya. Oleh karena itu kita harus menggunakan rumus garis potong hiperbolik dengan aturan rantai untuk menurunkannya:
![]()
Turunan dari x yang dipangkatkan menjadi 2 menghasilkan 2x, jadi turunan dari garis potong hiperbolik dari x kuadrat adalah:
![]()