Di sini Anda akan menemukan cara menurunkan garis potong suatu fungsi. Selain itu, Anda akan dapat melihat beberapa latihan yang diselesaikan langkah demi langkah pada turunan garis potong. Dan terakhir, Anda akan menemukan demonstrasi rumus turunan trigonometri jenis ini.
Apa turunan dari garis potong?
Turunan garis potong x sama dengan hasil kali garis potong x dan garis singgung x.
![]()
Dengan menerapkan rumus trigonometri, turunan garis potong x juga dapat didefinisikan sebagai hasil bagi sinus x dibagi kuadrat kosinus x.
![]()
Dan jika kita menerapkan aturan rantai, maka turunan garis potong suatu fungsi adalah hasil kali garis potong fungsi tersebut dikali garis singgung fungsi tersebut dikalikan dengan turunan fungsi tersebut.
![]()
Secara ringkas rumus turunan fungsi garis potong adalah sebagai berikut:
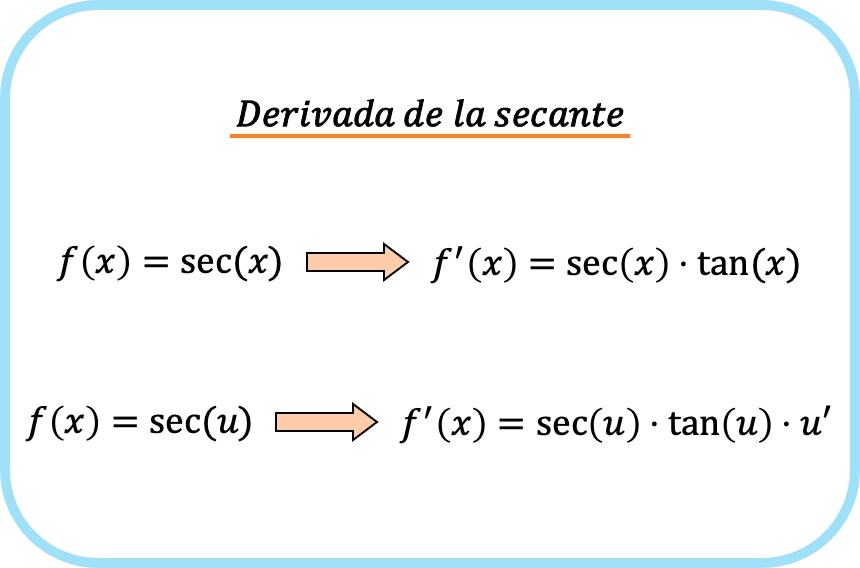
Contoh turunan dari garis potong
Setelah kita mengetahui rumus turunan garis potong, kita akan menyelesaikan beberapa contoh turunan trigonometri jenis ini.
Contoh 1: Turunan dari garis potong 2x
Dalam contoh ini kita akan melihat berapa nilai turunan dari garis potong 2x:
![]()
Untuk menurunkan garis potong fungsi 2x, Anda harus menggunakan rumus yang sesuai. Selain itu, dalam argumen garis potong kita mempunyai fungsi selain x, jadi kita perlu menerapkan aturan rantai.
![]()
Fungsi 2x linier, jadi turunannya adalah 2. Oleh karena itu, untuk mencari turunannya, kita cukup mengganti u dengan 2x dan u’ dengan 2 pada rumus:
![]()
Contoh 2: Turunan dari garis potong x kuadrat
Dalam latihan ini kita akan melihat turunan dari garis potong x kuadrat:
![]()
Untuk menurunkan garis potong suatu fungsi, Anda dapat menggunakan salah satu dari dua rumus yang terlihat di atas, namun dalam hal ini kita akan membedakan fungsi tersebut dengan rumus perkalian antara garis potong dan garis singgung.
![]()
Turunan x dipangkatkan 2 menghasilkan 2x, jadi turunan garis potong x kuadrat adalah:
![]()
Contoh 3: Turunan dari kubus potong suatu polinomial
![]()
Aturan turunan garis potong suatu fungsi adalah:
![]()
Namun dalam kasus ini kita harus menurunkan fungsi majemuk, karena garis potong dipangkatkan ketiga dan, terlebih lagi, dalam argumennya kita memiliki fungsi polinomial. Jadi, untuk membedakan seluruh fungsi, kita perlu menerapkan aturan rantai:
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)& =3\text{sec}^2(x^5+4x^2-3)\text{sec}(x^5+4x^2-3)\text{tan}(x^5+4x^2-3)(5x^4+8x)\\[1.5ex]&=3\text{sec}^3(x^5+4x^2-3)\text{tan}(x^5+4x^2-3)(5x^4+8x)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7ab88cc23ab3fb559e2386cd52637082_l3.png)
Latihan yang diselesaikan pada turunan dari garis potong
Turunkan fungsi garis potong berikut:
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{B) }f(x)& =4\text{sec}^3(5x^4)\cdot \text{sec}(5x^4)\cdot \text{tan}(5x^4)\cdot 20x^3\\[1.5ex] &=4\text{sec}^4(5x^4)\cdot \text{tan}(5x^4)\cdot 20x^3\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-72985d8bce95d808b9070bc7b834b271_l3.png)
![]()
![]()
![]()
Demonstrasi rumus turunan garis potong
Selanjutnya kita akan membuktikan rumus turunan garis potong. Meskipun jelas bahwa Anda tidak perlu hafal buktinya, ada baiknya Anda memahami dari mana rumus tersebut berasal.
Secara matematis, definisi garis potong adalah kebalikan perkalian dari kosinus:
![]()
Oleh karena itu, kita dapat mencoba menurunkan garis potong menggunakan aturan hasil bagi:
![]()
Dan, seperti yang kita lihat di bagian pertama, ekspresi sebelumnya dapat diubah menjadi rumus turunan dari garis potong. Untuk melakukannya, kita pisahkan pecahan menjadi dua pecahan yang berbeda:
![]()
Pembagian sinus dengan cosinus sama dengan tangen, oleh karena itu kita ganti hasil bagi tersebut dengan tangen:
![]()
Menurut definisi matematis dari fungsi garis potong, kosinus adalah perkalian kebalikannya. Jadi dengan mengganti satu dibagi cosinus dengan garis potong, kita mendapatkan rumus turunannya:
![]()