Pada artikel ini kami akan menunjukkan kepada Anda berapa turunan dari fungsi linier. Selain itu, kami menyelesaikan beberapa contoh turunan fungsi linier dan mendemonstrasikan rumus untuk jenis turunan ini. Anda bahkan akan menemukan latihan terpecahkan tentang turunan fungsi linier.
Apa turunan dari fungsi linier?
Turunan fungsi linier adalah koefisien suku derajat pertama , artinya turunan fungsi linier f(x)=Ax+B sama dengan A.
![]()
Suku bebas dihilangkan dari turunan karena turunan suatu konstanta adalah nol. Dan sebaliknya, turunan suatu suku derajat pertama adalah koefisien suku tersebut. Oleh karena itu, turunan dari jumlah kedua jenis fungsi tersebut adalah koefisien suku liniernya.
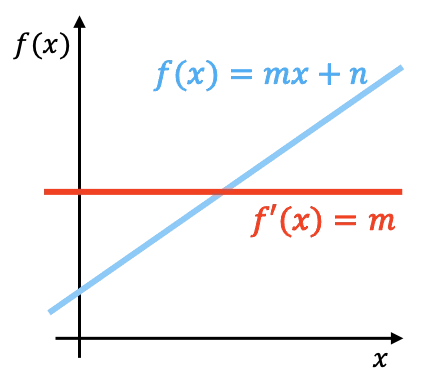
Secara geometris, turunan suatu fungsi linier adalah kemiringan fungsi tersebut. Pada grafik di atas Anda dapat melihat representasi fungsi linier dengan turunannya.
Contoh turunan fungsi linier
Mengingat definisi turunan fungsi linier, kita akan menghitung beberapa contoh fungsi linier untuk menyelesaikan pemahaman konsepnya:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=3x+1\quad\longrightarrow\quad f'(x)=3\\[3ex]f(x)=5x-4\quad\longrightarrow\quad f'(x)=5\\[3ex] f(x)=-2x+9\quad\longrightarrow\quad f'(x)=-2\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b12cfa0a6432f8171149ec0139d259ce_l3.png)
Perlu diingat bahwa turunan fungsi linier selalu berupa bilangan yang menyertai variabel x bila fungsi tersebut tidak mempunyai suku bebas, atau dengan kata lain hanya mempunyai satu suku berderajat satu. Misalnya:
![]()
Oleh karena itu, turunan fungsi linier adalah fungsi yang tidak memiliki variabel bebas, yaitu bilangan prima.
Bukti turunan fungsi linier
Selanjutnya kita akan mendemonstrasikan rumus turunan fungsi linier.
Misalkan f adalah sembarang fungsi linier:
![]()
Rumus untuk menghitung turunan suatu fungsi di suatu titik adalah:
![]()
Jadi, jika kita menghitung limit fungsi linier sebelumnya, kita mendapatkan:
![]()
Kami menyelesaikan tanda kurung:
![]()
Kami beroperasi di pembilang:
![]()
Dan terakhir, kita sederhanakan pecahannya:
![]()
Kesimpulannya, turunan fungsi linier sama dengan koefisien suku derajat pertama di titik mana pun. Dengan demikian, rumus turunan fungsi linier diturunkan.
Memecahkan masalah turunan fungsi linier
Hitung turunan dari fungsi linier berikut:
![]()
![]()
![]()
![]()
![]()
![]()
Untuk menurunkan fungsi linier, cukup hilangkan suku konstanta dan variabel dari fungsi tersebut, sehingga hanya koefisien suku liniernya yang tersisa. Belum:
![]()
![]()
![]()
![]()
![]()
![]()
Meskipun koefisien suatu fungsi adalah pecahan atau akar, penurunan fungsi linier dilakukan dengan cara yang sama.