▷ Apa yang dimaksud dengan trinomial persegi sempurna? (contoh)

Di halaman ini kami menjelaskan apa itu trinomial persegi sempurna dan cara penghitungannya. Selain itu, Anda akan dapat melihat beberapa contoh dan berlatih dengan latihan trinomial persegi sempurna langkah demi langkah.

Apa yang dimaksud dengan trinomial persegi sempurna?

Tentunya sebelum melihat pengertian trinomial persegi sempurna, Anda perlu mengetahui apa itu trinomial , jadi saya sarankan untuk melihat halaman tertaut ini (yang dijelaskan secara detail) sebelum melanjutkan.

Jadi, pengertian trinomial persegi sempurna adalah sebagai berikut:

Dalam matematika, trinomial kuadrat sempurna , juga dikenal sebagai TCP , adalah trinomial yang diperoleh dengan mengkuadratkan binomial.

Oleh karena itu, trinomial kuadrat sempurna terdiri dari polinomial dengan dua kuadrat sempurna dan suku lain yang merupakan hasil kali ganda dari alas kuadrat tersebut.

Seperti yang bisa Anda lihat dari dua rumus di atas, trinomial kuadrat sempurna diperoleh dari dua identitas penting (atau hasil kali penting), itulah mengapa ini sangat penting. Secara khusus, trinomial kuadrat sempurna ditemukan saat menyelesaikan kuadrat penjumlahan atau kuadrat pengurangan .

Contoh Trinomial Kuadrat Sempurna

Untuk menyelesaikan pemahaman konsep trinomial persegi sempurna, kami akan menjelaskan 2 contoh langkah demi langkah:

Contoh 1

$x^2+6x+9$

Contoh ini adalah trinomial kuadrat sempurna karena dalam ekspresi aljabarnya terdapat dua kuadrat sempurna (yaitu, keduanya mempunyai akar kuadrat eksak), karena

$x^2$

dan 9 setara dengan

$x$

dan 3 masing-masing dipangkatkan dua:

$(x)^2 = x^2$

$(3)^2 = 9$

Dan lebih lagi, sisa suku terakhir dari trinomial

$(6x)$

Itu diperoleh dengan mengalikan alas dua persegi sebelumnya dan dengan 2:

$2\cdot x \cdot 3 = 6x$

Jadi seluruh identitas penting yang lengkap dalam latihan ini adalah:

$(x+3)^2 =x^2+6x+9$

Contoh 2

$16x^2-40x+25$

Contoh lain ini juga merupakan trinomial kuadrat sempurna karena 3 syarat yang diperlukan terpenuhi: dua suku sama dengan dua kuadrat sempurna, dan suku lainnya adalah hasil perkalian alas persegi tersebut dengan 2.

$(4x)^2 = 16x^2$

$(5)^2 = 25$

$2\cdot 4x \cdot 5 =40x$

Dalam hal ini trinomial kuadrat sempurna mempunyai monomial negatif, oleh karena itu ia sesuai dengan perkembangan persamaan penting dari selisih kuadrat:

$(4x-5)^2 = 16x^2-40x+25$

Cara Memfaktorkan Trinomial Kuadrat Sempurna

Dalam aljabar, masalah yang sangat umum adalah memfaktorkan trinomial kuadrat sempurna (PCT). Jika Anda tidak tahu artinya, memfaktorkan polinomial berarti mengubah ekspresinya menjadi hasil kali faktor.

Jadi, untuk memfaktorkan jenis trinomial aljabar ini, aturan berikut harus dipatuhi:

Trinomial harus mempunyai dua kuadrat sempurna, yang akan kita sebut
$a^2$

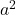
Dan

$b^2.$
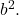
Suku ketiga trinomial yang tersisa harus sama dengan hasil kali ganda dari dua kuadrat sempurna, yang secara matematis sesuai dengan persamaan
$2\cdot a \cdot b.$
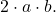
Trinomial yang difaktorkan adalah
$(a+b)^2$

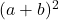
jika semua suku trinomial kuadrat sempurna adalah positif, sebaliknya jika hasil kali ganda alas kuadrat bertanda negatif maka trinomial yang difaktorkan adalah

$(a-b)^2.$

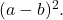
Untuk menyelesaikan pemahaman prosedurnya, kami akan menyelesaikan latihan langkah demi langkah:

Faktorkan trinomial kuadrat sempurna berikut:

$x^2-12x+36$

Hal pertama yang perlu kita lakukan adalah mengidentifikasi apakah trinomial tersebut memiliki dua elemen yang merupakan kuadrat sempurna, atau dengan kata lain, jika akar kuadratnya tidak menghasilkan angka desimal. Dalam masalah ini

$x^2$

adalah kuadrat variabel

$x$

dan 36 adalah kuadrat dari 6:

$\sqrt{x^2} = x$

$\sqrt{36} = 6$

Oleh karena itu, trinomial memiliki dua kuadrat sempurna.

Kedua, kita harus memeriksa apakah suku perantaranya ekuivalen dengan hasil kali ganda dari dua akar yang dihitung pada langkah sebelumnya:

$2 \cdot x \cdot 6 = 12x$

Aturan ini juga dipatuhi.

Maka semua syarat terpenuhi. Oleh karena itu, trinomial kuadrat sempurna yang difaktorkan adalah binomial yang dibentuk oleh dua akar yang ditemukan (

$x$

dan angka 6) kuadrat:

$x^2-12x+36=(x-6)^2$

Karena suku perantaranya negatif, kita juga harus memberi tanda minus di dalam tanda kurung. Di sisi lain, jika positif kita harus menambahkan jumlah:

$x^2+12x+36=(x+6)^2$

Logikanya, pemfaktoran adalah prosedur yang rumit, jadi selain mencoba melakukan latihan di bawah ini, saya sarankan untuk melihat contoh pemfaktoran polinomial berikut. Di tautan ini kami juga menjelaskan metode yang digunakan tidak hanya untuk memfaktorkan trinomial, tetapi juga semua jenis polinomial, dan dengan cepat.

Latihan soal trinomial persegi sempurna

Ubah trinomial berikut menjadi binomial persegi dengan menerapkan rumus yang sesuai:

$\text{A)} \ x^2+8x+16$

$\text{B)} \ x^2-14x+49$

$\text{C)} \ x^4-20x^2+100$

$\text{D)} \ 81x^2+90x+25$

$\text{E)} \ 64x^4-176x+121$

Lihat solusinya

Untuk mengubah trinomial kuadrat sempurna menjadi pangkat binomial kuadrat, Anda harus menggunakan rumus identitas penting kuadrat suatu jumlah dan kuadrat selisih, yaitu:

$(a+b)^2 = a^2+2ab+b^2$