Titik simetris terhadap titik lain, terhadap garis dan bidang

Di sini Anda akan menemukan cara menghitung titik simetri terhadap titik lain, terhadap garis, dan terhadap bidang. Selain itu, Anda akan dapat melihat contoh dan latihan yang diselesaikan langkah demi langkah.

Titik simetris ke titik lain

Sebelum kita melihat cara menghitung titik simetris, mari kita tinjau apa sebenarnya titik simetris terhadap titik lainnya:

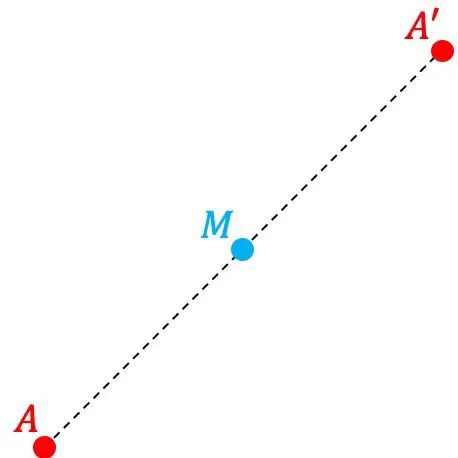
Titik A’ adalah titik simetris titik A terhadap titik M yang lain jika titik A’ terletak simetris, jarak dari titik M sama dengan jarak antara titik A dan M. Oleh karena itu, M adalah titik tengah ruas yang dibentuk oleh titik A dan A’.

titik yang simetris dengan titik lainnya

$d(A,M) = d(A',M )$

Sebaliknya, kita juga mengatakan bahwa titik M adalah pusat simetri.

Jadi, untuk menghitung koordinat titik simetrinya, kita akan menggunakan rumus titik tengah suatu ruas :

$\cfrac{A+A'}{2}=M$

Dari persamaan ini kita mengekstrak titik A’ yang tidak diketahui dan kita memperoleh rumus titik yang simetris terhadap titik lain:

$\color{orange} \boxed{ \color{black} \quad A' = 2M - A \quad \vphantom{\Bigl)}}$

Contoh mencari suatu titik yang simetris terhadap titik lain

Sebagai contoh, kita akan menghitung titik simetri titik A terhadap titik M. Perhatikan kedua titik tersebut:

$A(1,3,0) \qquad \qquad M(-1,4,2)$

Untuk menentukan titik simetri antara dua titik tersebut, kita terapkan rumus titik simetri terhadap titik lainnya:

$A' = 2M - A$

Sekarang kita ganti poin pada rumus:

$A' = 2(-1,4,2) -(1,3,0)$

Dan kami beroperasi:

$A' = (-2,8,4) -(1,3,0)$

$\bm{A'=(-3,5,4)}$

titik simetris terhadap garis lurus

Kita baru saja melihat gagasan tentang suatu titik yang simetris terhadap titik lainnya. Nah, titik simetris suatu titik terhadap suatu garis sangat mirip:

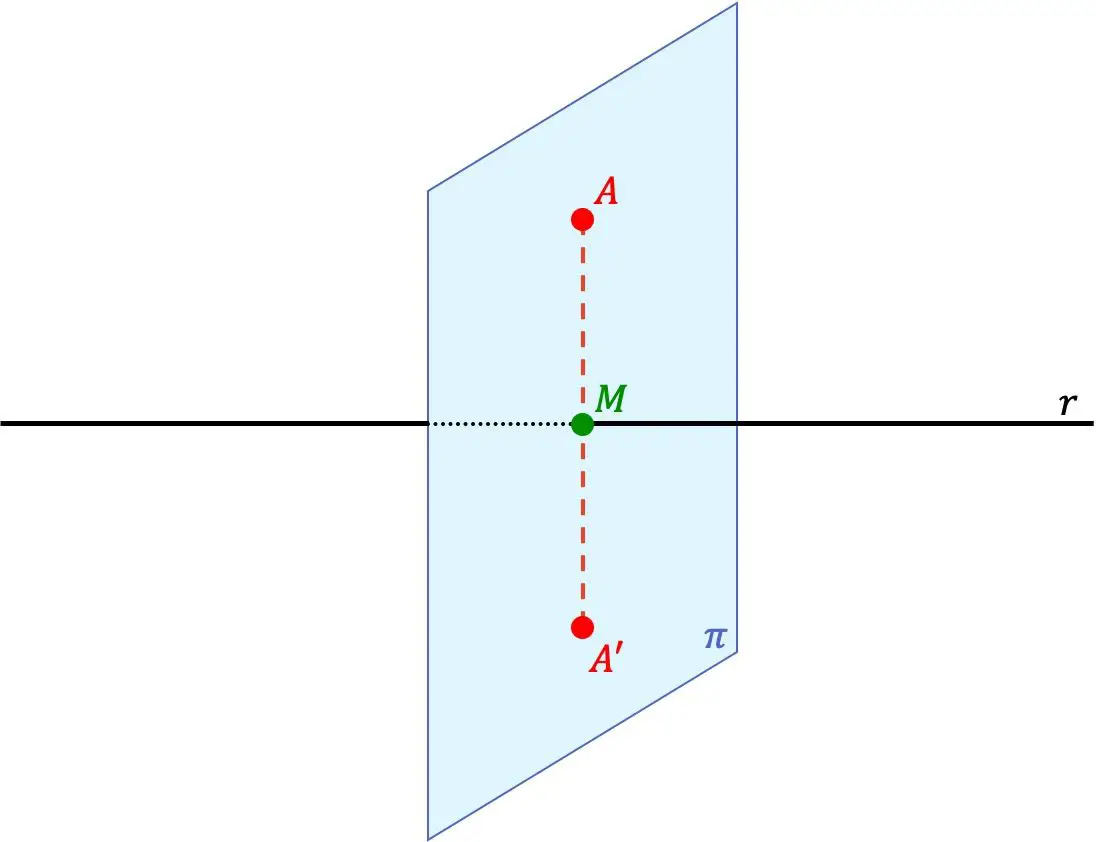
Titik A’ adalah titik simetris titik A terhadap suatu garis jika kedua titik A’ dan A terletak pada satu garis yang tegak lurus garis tersebut dan jarak antara titik A’ dan garis tersebut sama dengan jarak antara titik A dan garis.

$d(A,r)= d(A',r)$

Jadi garis r juga merupakan sumbu simetri antar titik.

Jadi, untuk menentukan titik simetri titik A terhadap garis r , kita harus mengikuti prosedur berikut:

Kita cari bidang yang tegak lurus terhadap garis r yang melalui titik A (bidang π dari representasi grafik sebelumnya). Untuk melakukan ini, kita harus menggunakan vektor arah garis, yang merupakan vektor normal bidang.
Kita hitung titik potong antara bidang yang ditemukan dengan garis (titik M pada gambar sebelumnya).
Kita menggunakan rumus titik simetris tentang titik (terlihat pada bagian di atas) untuk mencari titik simetris titik A terhadap titik M. Hasilnya adalah titik simetris yang kita cari.

Contoh menghitung titik simetri terhadap suatu garis

Setelah kita mengetahui cara menghitung titik simetri titik lain terhadap sebuah garis, kita akan melihat latihan yang diselesaikan sebagai contoh:

Tentukan titik simetris titik A terhadap garis r. Dikatakan titik dan garis:

$\displaystyle A(4,0,-1) \qquad \qquad r: \ \begin{cases}x=1 + t \\[1.7ex] y=5 +4t\\[1.7ex] z=-4-3t \end{cases}$

Pertama, kita perlu menghitung bidang yang tegak lurus garis r yang melalui titik A. Vektor yang normal pada bidang tersebut adalah vektor arah garis yang komponennya adalah suku-suku di depan parameter

$t$

karena dinyatakan dalam bentuk persamaan parametrik:

$\vv{n}=(1,4,-3)$

Dan koefisien A, B, dan C persamaan suatu bidang berimpit dengan koordinat vektor normalnya, oleh karena itu:

$\vv{n}=(1,4,-3) \quad \longrightarrow \quad \pi : \ 1x+4y-3z+D=0$

Titik A pasti terletak pada bidang ini, jadi sekarang kita dapat mensubstitusikan titik A ke dalam persamaan bidang tersebut untuk mencari koefisien D:

$A(4,0,-1)$

$4+4\cdot 0-3\cdot (-1)+D=0$

$4+3+D=0$

$7+D=0$

$D=-7$

Sehingga persamaan bidang yang tegak lurus garis ry yang melalui titik A adalah:

$\pi : \ x+4y-3z-7=0$

Setelah kita mengetahui persamaan bidangnya, kita perlu menghitung titik potong bidang dan garis. Untuk melakukan ini, kita substitusikan koordinat garis ke dalam persamaan bidang dan selesaikan persamaan yang dihasilkan:

$\displaystyle r: \ \begin{cases}x=1 + t \\[1.7ex] y=5 +4t\\[1.7ex] z=-4-3t \end{cases} \qquad \qquad \pi : \ x+4y-3z-7=0$

$(1+t)+4(5+4t)-3(-4-3t)-7=0$

$1+t+20+16t+12+9t-7=0$

$26t+26=0$

$26t=-26$

$t=\cfrac{-26}{26}$

$t=-1$

Sekarang kita ganti nilainya

$t$

diperoleh persamaan garis:

$\displaystyle t=-1 \ \longrightarrow \ \begin{cases}x=1 -1=0 \\[1.7ex] y=5 +4\cdot (-1)=1\\[1.7ex] z=-4-3\cdot (-1)=-1 \end{cases}$

Jadi titik potong antara garis r dan bidang yang tegak lurus adalah:

$M(0,1,-1)$

Terakhir, cukup mencari titik simetris titik A terhadap titik M; untuk ini, kita bisa menggunakan rumus yang terlihat di awal halaman ini:

$\begin{aligned} A' & = 2M - A \\[2ex] &= 2(0,1,-1) - (4,0,-1) \\[2ex] & = (0,2,-2)-(4,0,-1)\\[2ex] & = \bm{(-4,2,-1)} \end{aligned}$

titik simetris terhadap bidang

Sebelum melihat cara menentukan titik simetri suatu titik lain terhadap suatu bidang, mari kita lihat apa definisinya:

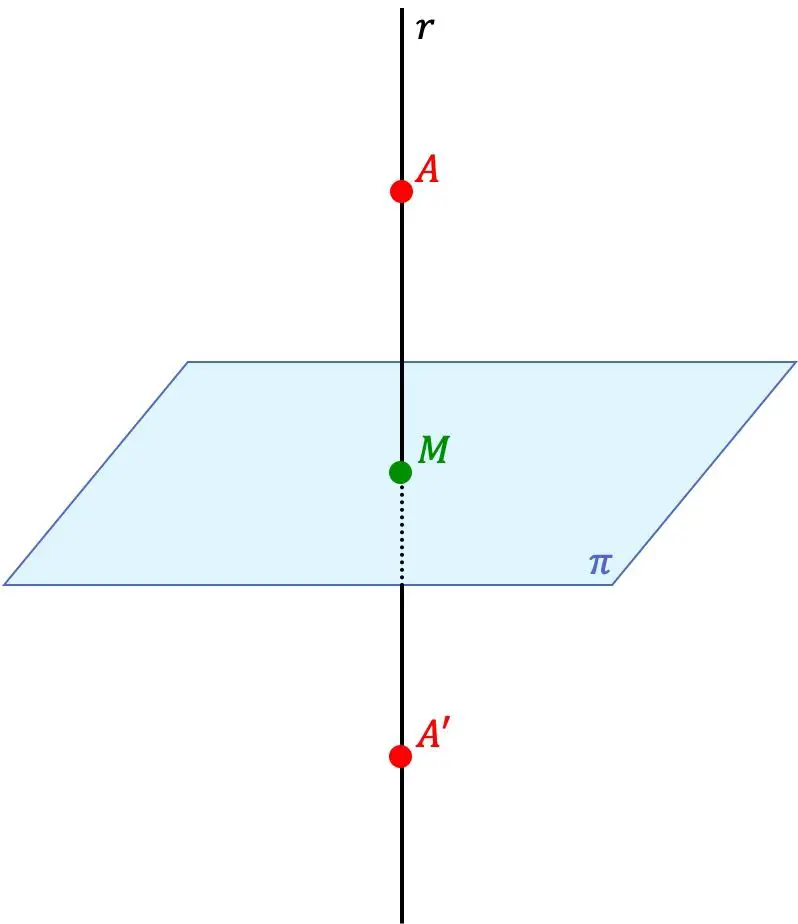
Titik A’ adalah titik simetris titik A terhadap sebuah bidang jika kedua titik A’ dan A terletak pada satu garis yang tegak lurus bidang tersebut dan jarak antara titik A’ dan bidang tersebut setara dengan jarak antara titik A dan bidang.

titik yang simetris terhadap titik lain yang relatif terhadap suatu bidang

$d(A,\pi)= d(A',\pi)$

Jadi bidang tersebut juga merupakan bidang simetri antara dua titik.

Jadi, untuk mengetahui koordinat Kartesius titik simetris titik A terhadap bidang π, Anda harus mengikuti langkah-langkah berikut:

Kita cari persamaan garis yang tegak lurus bidang yang melalui titik A. Untuk ini kita akan menggunakan vektor normal bidang sebagai vektor arah garis.
Kita hitung titik potong antara bidang dan garis yang ditemukan (titik M pada gambar sebelumnya).
Kita menggunakan rumus titik simetris tentang titik (terlihat di bagian awal) untuk mencari titik simetris titik A terhadap titik M. Hasilnya adalah titik simetris yang kita cari.

Contoh penentuan titik simetri terhadap suatu bidang

Di bawah ini Anda dapat melihat penyelesaian soal mengenai titik simetri titik lain terhadap bidang:

Tentukan titik simetri A terhadap bidang π. Karena itu poin dan rencana:

$\displaystyle A(3,-4,2) \qquad \qquad \pi: \ 2x+y-z-6=0$

Hal pertama yang perlu kita lakukan adalah mencari persamaan garis yang tegak lurus bidang dan melalui titik A. Untuk melakukannya, kita dapat menggunakan vektor normal bidang sebagai vektor arah garis, yang komponennya X, Y, Z adalah koefisien suku A, B dan C berturut-turut dari persamaan bidang:

$\pi: \ 2x+y-z-6=0 \quad \longrightarrow \quad \vv{n} = (2,1,-1)$

Sekarang kita dapat membuat persamaan parametrik garis ortogonal terhadap bidang dengan vektor arah ditemukan dan salah satu titiknya (titik A):

$\displaystyle r: \ \begin{cases}x=3 + 2t \\[1.7ex] y=-4 +t\\[1.7ex] z=2-t \end{cases}$

Setelah kita mengetahui garis tegak lurus, kita menghitung titik potong bidang dan garis dengan mensubstitusikan koordinat garis tersebut ke dalam persamaan bidang:

$\displaystyle r: \ \begin{cases}x=3 + 2t \\[1.7ex] y=-4 +t\\[1.7ex] z=2-t \end{cases} \qquad \qquad \pi : \ 2x+y-z-6=0$

$2(3+2t)+(-4+t)-(2-t)-6=0$

$6+4t-4+t-2+t-6=0$

$6t-6=0$

$6t=6$

$t=\cfrac{6}{6}$

$t=1$

Sekarang kita ganti nilainya

$t$

diperoleh persamaan garis:

$\displaystyle t=1 \ \longrightarrow \ \begin{cases}x=3 + 2\cdot 1 =5\\[1.7ex] y=-4 +1=-3\\[1.7ex] z=2-1=1 \end{cases}$

Jadi titik potong antara bidang dan garis tegak lurus adalah:

$M(5,-3,1)$

Terakhir, kita tinggal mencari titik simetris titik A terhadap titik M. Dan untuk melakukannya, kita dapat menggunakan rumus yang terlihat di awal halaman ini:

$\begin{aligned} A' & = 2M - A \\[2ex] &= 2(5,-3,1) - (3,-4,2) \\[2ex] & = (10,-6,2)-(3,-4,2)\\[2ex] & = \bm{(7,-2,0)} \end{aligned}$

Titik simetris terhadap titik lain, garis dan bidang