Pada halaman ini kami menjelaskan apa itu teorema faktor. Selain itu, kami menunjukkan untuk apa teorema faktor digunakan: pembagian polinomial, mencari akar, memfaktorkan polinomial, dll. Terakhir, Anda akan dapat berlatih dengan latihan langkah demi langkah tentang teorema faktor.
Apa teorema faktornya?
Dalam matematika, teorema faktor menyatakan bahwa suatu polinomial P(x) habis dibagi oleh polinomial lain yang berbentuk (xa) jika dan hanya jika P(a)=0.
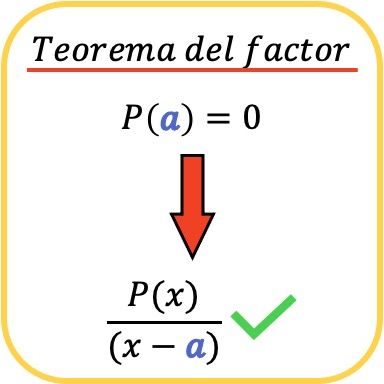
Demikian pula, sebagai akibat dari teorema faktor, maka jika suatu polinomial P(x) habis dibagi suku (x−a), maka nilai a adalah akar (atau nol) dari polinomial P( x ) .
Bahwa suatu polinomial habis dibagi oleh polinomial lain berarti sisa (atau sisa) pembagian antara kedua polinomial tersebut sama dengan nol. Jika Anda belum mengingat sepenuhnya konsep ini, di tautan berikut Anda dapat melihat contoh pembagian polinomial , di sana Anda juga akan menemukan penjelasan tentang cara membagi polinomial dan latihan yang diselesaikan langkah demi langkah.
Contoh Teorema Faktor
Sekarang setelah kita mengetahui definisi matematis dari teorema faktor, mari kita lihat beberapa contoh untuk mengetahui cara penerapannya.
Contoh 1
Salah satu penerapan teorema faktor adalah untuk mengetahui apakah suatu polinomial tertentu habis dibagi binomial . Mari kita lihat contoh bagaimana hal ini dilakukan dengan teorema faktor:
- Tentukan apakah polinomial P(x) habis dibagi binomial Q(x), keduanya adalah:
![]()
Pertama, polinomial pembagi, Q(x), adalah polinomial bertipe (xa), sehingga kita dapat menerapkan teorema faktor untuk menyelesaikan soal tersebut.
Jadi, untuk memeriksa apakah P(x) dapat dibagi dengan Q(x) kita perlu menghitung nilai numerik dari polinomial P(x) untuk x=1, karena 1 adalah suku bebas dari polinomial pembagi yang tandanya diubah :
![Rendered by QuickLaTeX.com \begin{aligned} P(1) & =1^2-4\cdot 1+3 \\[2ex] & = 1-4+3 \\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-00216efc4a2e53b0b38de1175e73a5bd_l3.png)
Nilai numerik polinomial P(x) pada x = 1 menghasilkan nol, sehingga menurut teorema faktor P(x) habis dibagi Q(x), atau dengan kata lain sisa pembagian keduanya adalah nol.
Kita dapat memverifikasi bahwa kondisi pembagian terpenuhi dengan membagi 2 polinomial dengan teorema Ruffini :
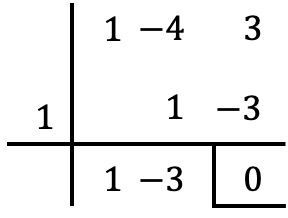
Seperti yang Anda lihat dalam contoh ini, teorema faktor adalah kasus khusus dari teorema sisa (atau sisa). Saya meninggalkan artikel ini untuk Anda yang menjelaskan apa itu teorema sisa , Anda juga akan menemukan contoh dan latihan yang diselesaikan dengannya. Dan terlebih lagi, Anda akan dapat melihat perbedaan antara teorema sisa dan teorema faktor.
Contoh 2
Teorema faktor juga dapat digunakan untuk mencari akar (atau nol) suatu polinomial. Namun, tentunya untuk memahami masalah seperti ini Anda perlu mengetahui apa itu akar-akar polinomial . Jika Anda masih belum memahami konsep ini, Anda dapat melihat halaman tertaut yang dijelaskan secara detail.
Jadi mari kita lihat contoh bagaimana teorema faktor diterapkan untuk mencari akar polinomial:
- Diketahui polinomial P(x), hitunglah jika salah satu akarnya adalah x=2:
![]()
Dengan menerapkan teorema faktor, suku x=2 hanya akan menjadi akar polinomial P(x) jika nilai numerik P(x) untuk x=2 adalah nol. Jadi kita perlu mencari nilai numerik ini:
![Rendered by QuickLaTeX.com \begin{aligned} P(2) & =2^3-3\cdot 2^2+5\cdot 2-6 \\[2ex] & = 8-3\cdot 4 +5\cdot 2 -6\\[2ex] & = 8-12+10-6 \\[2ex] & = 0\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-82d50f0361613cb6c540051f8da4bc20_l3.png)
Memang benar, nilai numerik polinomial P(x) hilang pada x=2, jadi berkat teorema faktor kita dapat menegaskan bahwa x=2 adalah akar dari polinomial P(x).
Memfaktorkan Polinomial Menggunakan Teorema Faktor
Penerapan lain dari teorema faktor adalah pemfaktoran polinomial . Jika Anda tidak tahu apa itu, memfaktorkan polinomial berarti mengubah ekspresi polinomial menjadi produk faktor, yaitu memfaktorkan polinomial menyederhanakan ekspresi aljabarnya.
Jadi, teorema faktorial menetapkan bahwa jika suatu polinomial P(x) memenuhi P(a)=0 untuk suatu nilai a tertentu, maka ekspresi polinomial tersebut dapat difaktorkan ke dalam hasil kali P(x)=(xa)· Q( x), dimana Q(x) adalah polinomial hasil pembagian polinomial P(x) dengan (xa).
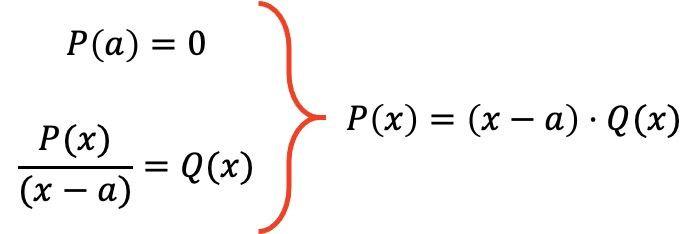
Sebagai contoh, kita akan memfaktorkan polinomial berikut menggunakan teorema faktorial:
![]()
Dari polinomial sebelumnya, kita dapat mengetahui bahwa x=-2 adalah salah satu akarnya, karena nilai numerik polinomial untuk x=-2 sama dengan nol:
![Rendered by QuickLaTeX.com \begin{aligned} P(-2) & =(-2)^3+2\cdot (-2)^2+4\cdot (-2)+8 \\[2ex] & =-8+2\cdot 4+4\cdot (-2)+8 \\[2ex] & = -8+8-8+8 \\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1d94a4657a385e672badeabd7458b376_l3.png)
Oleh karena itu, dengan aturan Ruffini, kita membagi polinomial P(x) antara binomial yang dibentuk oleh x dan akar ini berubah tanda, yaitu faktor (x+2):
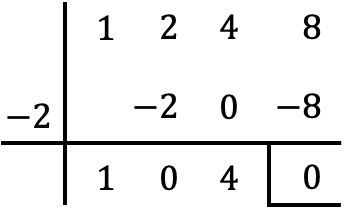
Jadi hasil bagi pembagian polinomial adalah:
![]()
Dan terakhir, dari teorema faktor, kita dapat menyatakan polinomial P(x) sebagai perkalian faktor (x+2) dengan hasil bagi yang diperoleh pada pembagian sebelumnya:
![]()
Kita telah memfaktorkan polinomial P(x), tetapi hanya sebagian. Untuk memfaktorkan suatu polinomial secara lengkap, prosedur yang lebih panjang harus diterapkan. Kami telah membuat panduan di mana kami mengajarkan langkah demi langkah cara memfaktorkan polinomial Ruffini , selain itu, dalam artikel ini kami telah menjelaskan semua jenis faktorisasi dan Anda akan dapat berlatih dengan latihan yang diselesaikan. Jadi klik tautannya untuk mengetahui cara memfaktorkan polinomial dari himpunan.
Soal Teorema Faktor Terpecahkan
Kemudian, kami telah menyiapkan beberapa latihan yang diselesaikan langkah demi langkah pada teorema faktor sehingga Anda dapat berlatih, dan memeriksa apakah Anda telah memahami teorema ini. Kami menyarankan Anda mencoba melakukannya sendiri dan kemudian melihat apakah Anda memahami solusinya dengan benar. Juga jangan lupa bahwa Anda dapat meninggalkan pertanyaan Anda di bawah di komentar! ❓❓💬💬
Latihan 1
Gunakan teorema faktorial untuk mencari tahu apakah polinomial P(x) habis dibagi binomial Q(x) dan, jika ya, carilah akar polinomial tersebut dan faktorkan.
![]()
Dalam hal ini, pembagi polinomial Q(x) adalah binomial yang hanya terdiri dari x dan suku bebas. Jadi untuk menunjukkan bahwa polinomial P(x) dapat dibagi dengan polinomial lain Q(x) dengan teorema faktorial, kita harus mengevaluasi nilai numerik dari polinomial P(x) dalam suku bebas dari tanda perubahan polinomial pembagi, artinya pada x=3:
![Rendered by QuickLaTeX.com \begin{aligned} P(3) & =2\cdot 3^3-4\cdot 3^2+3-7\\[2ex] & = 2\cdot 27-4\cdot 9+3-7 \\[2ex] & = 54-36+3-7\\[2ex] & = 14 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e8ac752f8e16fae1d66386e9d2a02a0_l3.png)
Nilai numerik polinomial P(x) pada x=3 setara dengan 14, artinya berbeda dengan nol. Jadi, menurut teorema faktor, P(x) TIDAK habis dibagi Q(x) karena sisa pembagiannya tidak nol.
Latihan 2
Cari tahu dengan teorema faktorial apakah polinomial P(x) habis dibagi binomial Q(x) dan, jika ya, carilah akar polinomial P(x) dan faktorkan.
![]()
Dalam hal ini pembagi polinomial Q(x) adalah binomial yang hanya terdiri dari x dan suku bebas, oleh karena itu kita dapat menerapkan teorema faktorial.
Dan untuk memeriksa apakah polinomial P(x) dapat dibagi dengan polinomial Q(x), kita harus mencari nilai numerik dari polinomial P(x) untuk suku bebas dari polinomial Q(x) yang tandanya diubah, yaitu yaitu, pada x=-1:
![Rendered by QuickLaTeX.com \begin{aligned} P(-1) & =(-1)^3+5\cdot (-1)^2+3\cdot (-1)-1\\[2ex] & = -1+5\cdot 1+3\cdot (-1)-1\\[2ex] & = -1+5-3-1\\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-34b63772a1b44bee2c746d94b6ca4785_l3.png)
Dalam soal ini, nilai numerik polinomial di x=-1 adalah nol, jadi P(x) habis dibagi Q(x).
Kemudian, kita dapat menyimpulkan dengan teorema faktorial bahwa x=-1 adalah akar dari polinomial P(x), karena nilai numerik P(x) pada x=-1 hilang.
Jadi, karena x=-1 adalah akar polinomial P(x), untuk memfaktorkannya, cukup membaginya dengan x+1. Dan untuk ini, kita akan menggunakan metode Ruffini:
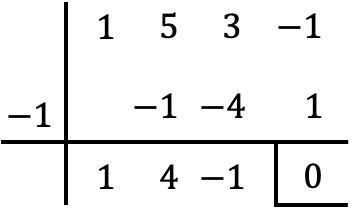
Jadi hasil operasinya adalah:
![]()
Oleh karena itu, kita dapat memfaktorkan polinomial P(x) sebagai berikut:
![]()
Latihan 3
Temukan dengan teorema faktorial apakah polinomial P(x) habis dibagi binomial Q(x) dan, jika ya, cari juga akar polinomial P(x) dan faktorkan.
![]()
Dalam hal ini polinomial yang membagi Q(x) adalah binomial yang hanya dibentuk oleh x dan suku bebas, sehingga kita dapat menggunakan teorema faktor.
Dan untuk memeriksa apakah polinomial P(x) habis dibagi polinomial Q(x), kita harus menentukan nilai numerik dari polinomial P(x) untuk suku bebas dari polinomial Q(x) yang tandanya berubah, yaitu- yaitu pada x =-3:
![Rendered by QuickLaTeX.com \begin{aligned} P(-3) & =(-3)^3+5\cdot (-3)^2+4\cdot (-3)-6\\[2ex] & = -27+5\cdot 9+4\cdot (-3)-6\\[2ex] & = -27+45-12-6\\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ef8bb895fe041193d71351ffadb94f2f_l3.png)
Dalam hal ini, nilai numerik polinomial pada x=-3 adalah nol, jadi memang P(x) habis dibagi Q(x).
Oleh karena itu, kita menyimpulkan dari teorema faktorial bahwa x=-3 adalah akar dari polinomial P(x), karena P(-3) sama dengan nol.
Jadi, karena x=-3 adalah akar polinomial P(x), untuk memfaktorkannya kita harus membaginya dengan x+3. Dan untuk ini, kita akan menggunakan aturan Ruffini:
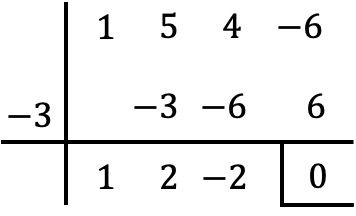
Jadi hasil pembagiannya adalah:
![]()
Oleh karena itu, kita dapat memfaktorkan polinomial P(x) dengan cara berikut:
![]()
Apa pendapat Anda tentang teorema faktor? Apakah menurut Anda ini berguna dalam aljabar? Kami membaca Anda di komentar!
👀⬇⬇⬇👀