Pada artikel ini Anda akan menemukan definisi teorema Weierstrass. Selain itu, Anda akan dapat berlatih dengan beberapa latihan yang diselesaikan selangkah demi selangkah dari teorema Weierstrass untuk memahaminya dengan sempurna.
Pernyataan teorema Weierstrass
Teorema Weierstrass mengatakan bahwa jika suatu fungsi kontinu pada interval tertutup, maka fungsi tersebut mempunyai maksimum absolut dan minimum absolut pada interval tersebut.
➤ Lihat: Apa yang dimaksud dengan fungsi kontinu?
Teorema Weierstrass hanya menyatakan bahwa ada maksimum dan minimum, tetapi tidak berguna untuk menghitung nilai titik-titik tersebut.
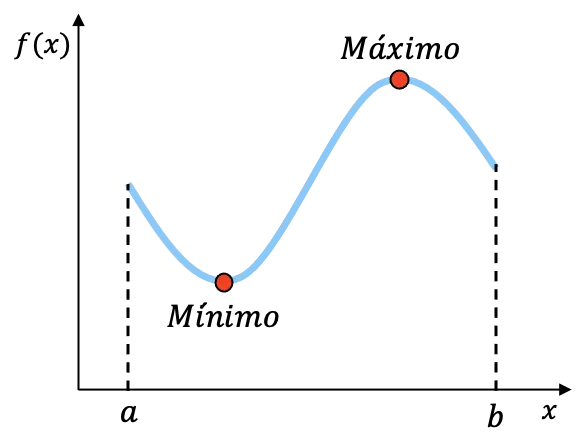
Misalnya, fungsi pada grafik di atas kontinu pada interval [a,b] dan mempunyai minimum dan maksimum pada interval tersebut. Meskipun kita tidak dapat mengetahui secara pasti koordinat kedua titik tersebut, kita mengetahui bahwa fungsi tersebut mempunyai dua titik akhir pada intervalnya.
➤ Lihat: cara menghitung maksimum dan minimum suatu fungsi
Karena fungsi tersebut kontinu pada seluruh interval, ini berarti fungsi tersebut juga akan mengambil semua nilai yang mungkin antara minimum absolut dan maksimum absolut pada interval yang sama.
Lebih jauh lagi, sebagai konsekuensi dari teorema Weierstrass, kita dapat menyimpulkan bahwa setiap fungsi kontinu pada interval tertutup dibatasi di atas dan di bawah , dan batas atas dan bawah fungsi masing-masing adalah maksimum dan minimum absolut.
Secara matematis teorema Weierstrass dapat dinyatakan sebagai berikut:
Emas
Dan
adalah dua titik yang disertakan (masing-masing titik minimum absolut dan maksimum absolut) dalam interval tertutup
![[a,b]](https://mathority.org/wp-content/ql-cache/quicklatex.com-fcda5ef4ae327e1afef79dc73df91703_l3.png "Rendered by QuickLaTeX.com")
di mana fungsinya didefinisikan.
Pembuktian teorema Weierstrass cukup rumit dan tidak memberikan kontribusi banyak terhadap konsep tersebut, sehingga tidak akan kami jelaskan pada artikel ini. Yang penting Anda memahami apa itu teorema Weierstrass dan kegunaannya.
Teorema Weierstrass Memecahkan Masalah
Latihan 1
Tentukan apakah fungsi berikut dibatasi pada interval yang diusulkan:
![f(x)=\log_3(x-4) \qquad x \in [5,10]](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e6a705ea1c5d586cf31d683ac7ccc85_l3.png "Rendered by QuickLaTeX.com")
➤ Lihat: domain fungsi logaritma
Kita dapat menentukan apakah suatu fungsi dibatasi pada interval [5,10] dengan menerapkan teorema Weierstrass. Oleh karena itu kita harus mengetahui apakah fungsi tersebut kontinu dalam interval ini, untuk melakukannya, kita menghitung domain dari fungsi logaritma:
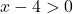
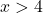
Fungsi tersebut kontinu untuk semua nilai yang lebih besar dari x=4, sehingga kontinu pada interval [5,10].
Oleh karena itu, fungsi tersebut memenuhi teorema Weierstrass pada interval [5,10], yang berarti dibatasi di atas dan di bawah interval ini.
Latihan 2
Tentukan apakah fungsi berikut mempunyai maksimum dan/atau minimum pada interval yang diusulkan:
![f(x)=\cfrac{3x^2-4}{2x-4} \qquad x \in [-3,3]](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f2e72f629bae2c39821ddbfbf6c93fc_l3.png "Rendered by QuickLaTeX.com")
➤ Lihat: domain fungsi rasional
Pertama, kita menganalisis kontinuitas fungsi rasional:
Namun, fungsi tersebut menyajikan diskontinuitas pada x=2, yang berarti bahwa fungsi tersebut tidak kontinu pada interval [-3,3].
Singkatnya, fungsi tersebut tidak memenuhi teorema Weierstrass sehingga kita tidak dapat mengatakan apakah fungsi tersebut memiliki minimum atau maksimum dalam interval ini.
Latihan 3
Tentukan apakah fungsi berikut mempunyai maksimum dan/atau minimum dalam interval yang diusulkan dan hitung titik-titik ini:
![f(x)=x^2+3 \qquad x \in [0,4]](https://mathority.org/wp-content/ql-cache/quicklatex.com-4dd0cf4151f8b5c1b4e69be89b7a71e1_l3.png "Rendered by QuickLaTeX.com")
➤ Lihat: ciri-ciri fungsi kuadrat
Domain dari setiap fungsi kuadrat adalah semua bilangan real:
Oleh karena itu, fungsi tersebut kontinu pada interval [0,4] dan memenuhi teorema Weierstrass. Oleh karena itu, fungsi tersebut mempunyai minimum absolut dan maksimum absolut pada interval ini.
Selain itu, titik puncak parabola ini tepat di x=0, sehingga fungsinya meningkat tajam pada interval [0,4] dan akibatnya, minimumnya ada di x=0 dan maksimumnya di x= 4 .
Karl Weierstrass
Setelah kita melihat apa yang dimaksud dengan teorema Weierstrass, kami akan menjelaskan secara singkat siapa inventarisasi teorema ini.
Karl Theodor Wilhelm Weierstrass adalah seorang matematikawan Jerman yang sangat penting pada abad ke-19, lebih tepatnya ia lahir pada tanggal 31 Oktober 1815 di Ostenfelde dan meninggal pada tanggal 19 Februari 1897 di Berlin.
Selain teorema Weierstrass, ia juga dikenal karena kontribusinya yang lain pada matematika. Diantaranya, ia memberikan definisi kontinuitas, limit dan turunan, tiga konsep fungsi yang sangat penting.
Demikian pula, ia berhasil mendemonstrasikan teorema tertentu yang saat itu belum terverifikasi secara matematis, seperti teorema Bolzano-Weierstrass, teorema nilai rata-rata, atau teorema Heine-Borel.
Yang membuat penasaran, ada kawah bulan dan asteroid yang dinamai Weierstrass untuk menghormatinya.