Teorema rouche – frébenius

Di halaman ini kita akan mempelajari apa itu teorema Rouché Frobenius dan cara menghitung pangkat suatu matriks dengannya. Anda juga akan menemukan contoh dan latihan yang diselesaikan langkah demi langkah dengan teorema Rouché-Frobenius.

Apa yang dimaksud dengan teorema Rouché–Frobenius?

Teorema Rouché-Frobenius adalah metode untuk mengklasifikasikan sistem persamaan linear. Dengan kata lain, teorema Rouché-Frobenius digunakan untuk mengetahui berapa banyak solusi yang dimiliki suatu sistem persamaan tanpa harus menyelesaikannya.

Ada 3 jenis sistem persamaan:

  • System Kompatibel Ditentukan (SCD): Sistem memiliki solusi unik.
  • Sistem kompatibel tak tentu (ICS): sistem yang mempunyai solusi tak terhingga.
  • Sistem Tidak Kompatibel (SI): Sistem tidak memiliki solusi.

Selain itu, teorema Rouché-Frobenius nantinya juga memungkinkan kita menyelesaikan sistem menggunakan aturan Cramer .

Pernyataan teorema Rouché-Frobenius

Teorema Rouché-Frobenius mengatakan demikian

\displaystyle \bm{A}

adalah matriks yang dibentuk oleh koefisien-koefisien yang tidak diketahui dari suatu sistem persamaan. dan perut

\displaystyle \bm{A'}

, atau matriks diperluas , adalah matriks yang dibentuk oleh koefisien-koefisien yang tidak diketahui dari suatu sistem persamaan dan suku-suku bebasnya:

Teorema Rouché-Frobenius memungkinkan kita mengetahui jenis sistem persamaan apa yang kita hadapi berdasarkan pangkat matriks A dan A’:

  • Jika peringkat(A) = peringkat(A’) = jumlah yang tidak diketahui ⟶ Sistem kompatibel yang ditentukan (SCD)
  • Jika peringkat(A) = peringkat(A’) < jumlah yang tidak diketahui ⟶ Sistem kompatibel tak tentu (SCI)
  • jika rentang(A)

    \bm{\neq}

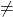
    rentang (A’) ⟶ Sistem tidak kompatibel (SI)

Setelah kita mengetahui apa yang dikatakan teorema Rouché-Frobenius, kita akan melihat cara menyelesaikan latihan teorema Rouché-Frobenius. Berikut 3 contohnya: latihan yang diselesaikan menggunakan teorema setiap jenis sistem persamaan.

Contoh sistem kompatibel yang ditentukan (SCD)

\begin{cases} 2x+y-3z=0 \\[1.5ex] x+2y-z= 1 \\[1.5ex] 4x-2y+z = 3\end{cases}

Matriks A dan matriks perluasan A’ dari sistem tersebut adalah:

\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 1 & 2 & -1 & 1 \\[1.1ex] 4 & -2 & 1 & 3\end{array} \right)

Sekarang kita menghitung rank matriks A. Untuk melakukannya, kita periksa apakah determinan seluruh matriks berbeda dari 0:

\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{vmatrix} = 25 \neq 0

Karena matriks mempunyai determinan 3×3 yang berbeda dengan 0, maka matriks A mempunyai rank 3:

\displaystyle rg(A)=3

Setelah kita mengetahui pangkat A, kita hitung pangkat A’, yang mana paling tidak pangkatnya adalah 3 karena kita baru saja melihat bahwa di dalamnya terdapat determinan berorde 3 yang berbeda dengan 0. Selain itu, tidak mungkin pangkatnya 4, karena kita tidak dapat membuat determinan berorde 4. Oleh karena itu, matriks A’ juga berperingkat 3:

\displaystyle rg(A')=3

Jadi, karena pangkat dari matriks A sama dengan pangkat dari matriks A’ dan dengan banyaknya sistem yang tidak diketahui (3), kita mengetahui melalui teorema Rouché Frobenius bahwa ini adalah Sistem Penentuan Kompatibel (SCD) :

\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}

Contoh sistem kompatibel tak tentu (ICS)

\begin{cases} x-y+2z=1 \\[1.5ex] 3x+2y+z= 5 \\[1.5ex] 2x+3y-z = 4\end{cases}

Matriks A dan matriks perluasan A’ dari sistem tersebut adalah:

\displaystyle A= \left( \begin{array}{ccc} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & -1 & 2 & 1 \\[1.1ex] 3 & 2 & 1 & 5 \\[1.1ex] 2 & 3 & -1 & 4 \end{array} \right)

Sekarang kita menghitung rank matriks A. Untuk melakukannya, kita periksa apakah determinan seluruh matriks berbeda dari 0:

\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{vmatrix} = 0

Penentu seluruh matriks A menghasilkan 0, sehingga tidak berpangkat 3. Untuk mengetahui apakah matriks tersebut berpangkat 2, kita harus mencari submatriks di A yang determinannya berbeda dengan 0. Misalnya dari pojok kiri atas :

\displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0

Karena matriks mempunyai determinan 2×2 yang berbeda dengan 0, maka matriks A mempunyai rank 2:

\displaystyle rg(A)=2

Setelah kita mengetahui pangkat A, kita menghitung pangkat A’. Kita sudah tahu bahwa determinan dari 3 kolom pertama menghasilkan 0, jadi kita coba kemungkinan determinan 3×3 lainnya:

\displaystyle \begin{vmatrix}1 & -1 & 1 \\[1.1ex] 3 & 2 & 5 \\[1.1ex] 2 & 3 & 4\end{vmatrix} = 0 \quad \begin{vmatrix}1 & 2 & 1 \\[1.1ex] 3 & 1 & 5 \\[1.1ex] 2 & -1 & 4\end{vmatrix} = 0 \quad \begin{vmatrix} -1 & 2 & 1 \\[1.1ex] 2 & 1 & 5 \\[1.1ex] 3 & -1 & 4\end{vmatrix} = 0

Semua determinan matriks A’ berukuran 3×3 adalah 0, sehingga matriks A’ juga tidak menduduki rangking 3. Namun di dalamnya memang terdapat determinan orde 2 yang berbeda dengan 0. Contoh:

\displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0

Jadi matriks A’ akan mempunyai rangking 2 :

\displaystyle rg(A')=2

Luas matriks A sama dengan luas matriks A’ tetapi luasnya lebih kecil dari jumlah yang tidak diketahui dalam sistem (3). Oleh karena itu, menurut teorema Rouché-Frobenius, ini adalah sistem kompatibel tak tentu (ICS):

\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}

Contoh sistem yang tidak kompatibel (IS)

\begin{cases} 2x+y-2z=3 \\[1.5ex] 3x-2y+z= 2 \\[1.5ex] x+4-5z = 3 \end{cases}

Matriks A dan matriks perluasan A’ dari sistem tersebut adalah:

\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -2 & 3 \\[1.1ex] 3 & -2 & 1 & 2 \\[1.1ex] 1 & 4 & -5 & 3 \end{array} \right)

Sekarang kita menghitung rank matriks A. Untuk melakukannya, kita periksa apakah determinan seluruh matriks berbeda dari 0:

\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{vmatrix} = 0

Penentu seluruh matriks A menghasilkan 0, sehingga tidak berpangkat 3. Untuk mengetahui apakah matriks tersebut berpangkat 2, kita harus mencari submatriks di A yang determinannya berbeda dengan 0. Misalnya dari pojok kiri atas :

\displaystyle \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & -2 \end{vmatrix} = -7 \neq 0

Karena matriks mempunyai determinan orde 2 yang berbeda dengan 0, maka matriks A mempunyai rank 2:

\displaystyle rg(A)=2

Setelah kita mengetahui pangkat A, kita menghitung pangkat A’. Kita sudah tahu bahwa determinan dari 3 kolom pertama menghasilkan 0, jadi sekarang kita coba, misalnya, dengan determinan dari 3 kolom terakhir:

\displaystyle \begin{vmatrix} 1 & -2 & 3 \\[1.1ex] -2 & 1 & 2 \\[1.1ex] 4 & -5 & 3 \end{vmatrix} = 3 \neq 0

Sebaliknya matriks A’ memang mengandung determinan yang hasilnya berbeda dengan 0, sehingga matriks A’ mempunyai rank 3 :

\displaystyle rg(A')=3

Oleh karena itu, karena pangkat matriks A lebih kecil daripada pangkat matriks A’, berdasarkan teorema Rouché-Frobenius kita menyimpulkan bahwa matriks tersebut merupakan Sistem Tidak Kompatibel (SI) :

\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}

Memecahkan masalah teorema Rouché – Frobenius

Latihan 1

Tentukan jenis sistem persamaan berikut dengan 3 yang tidak diketahui menggunakan teorema Rouché-Frobenius:

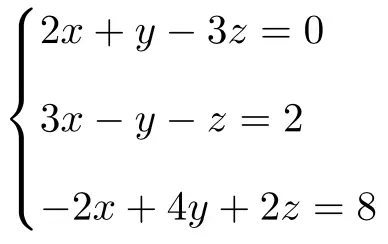
Latihan teorema Rouche - frobenius

Pertama-tama kita buat matriks A dan matriks perluasan A’ dari sistem:

\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 3 & -1 & -1 & 2 \\[1.1ex] -2 & 4 & 2 & 8 \end{array} \right)

Sekarang kita harus mencari rank matriks A. Untuk melakukannya, kita periksa apakah determinan matriks tersebut berbeda dari 0:

\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{vmatrix} = -4+2-36+6+8-6=-30 \bm{\neq 0}

Matriks yang mempunyai determinan orde ketiga selain 0, matriks A mempunyai rangking 3:

\displaystyle rg(A)=3

Setelah kita mengetahui pangkat A, kita menghitung pangkat A’. Ini setidaknya akan berada pada peringkat 3, karena kita baru saja melihat bahwa di dalamnya terdapat determinan berorde 3 yang berbeda dari 0. Selain itu, ia tidak mungkin berada pada peringkat 4, karena kita tidak dapat tidak membuat determinan 4×4. Oleh karena itu, matriks A’ juga mempunyai rangking 3:

\displaystyle rg(A')=3

Jadi, berkat teorema Rouché-Frobenius, kita mengetahui bahwa ini adalah sistem yang kompatibel dengan determinasi (SCD), karena jangkauan A sama dengan jangkauan A’ dan jumlah yang tidak diketahui.

\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}

Latihan 2

Klasifikasikan sistem persamaan berikut dengan 3 hal yang tidak diketahui menggunakan teorema Rouché-Frobenius:

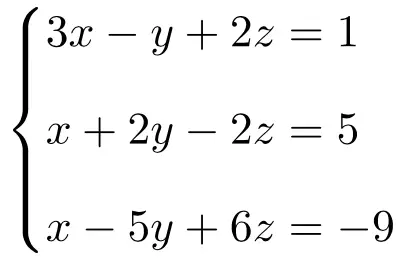
Latihan terpecahkan dari teorema Rouche-Frobenius

Pertama-tama kita buat matriks A dan matriks perluasan A’ dari sistem:

\displaystyle A= \left( \begin{array}{ccc}3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -1 & 2 & 1 \\[1.1ex] 1 & 2 & -2 & 5 \\[1.1ex] 1 & -5 & 6 & -9 \end{array} \right)

Sekarang mari kita hitung jangkauan matriks A:

\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{vmatrix} = 0

\displaystyle \begin{vmatrix} 3 & -1 \\[1.1ex] 1 & 2 \end{vmatrix} = 7 \neq 0

Jadi matriks A mempunyai rangking 2:

\displaystyle rg(A)=2

Setelah kita mengetahui pangkat A, kita menghitung pangkat A’. Kita sudah tahu bahwa determinan dari 3 kolom pertama menghasilkan 0, jadi kita coba kemungkinan determinan 3×3 lainnya:

\displaystyle \begin{vmatrix}-1 & 2 & 1 \\[1.1ex] 2 & -2 & 5 \\[1.1ex] -5 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix}3 & 2 & 1 \\[1.1ex] 1 & -2 & 5 \\[1.1ex] 1 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix} 3 & -1 & 1 \\[1.1ex] 1 & 2 & 5 \\[1.1ex] 1 & -5 & -9\end{vmatrix} = 0

Semua determinan matriks A’ berukuran 3×3 adalah 0, sehingga matriks A’ juga tidak menduduki rangking 3. Namun di dalamnya terdapat banyak determinan orde 2 yang berbeda dengan 0. Contoh:

\displaystyle \begin{vmatrix} -1 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -2 \neq 0

Jadi matriks A’ akan mempunyai rangking 2 :

\displaystyle rg(A')=2

Pangkat matriks A sama dengan pangkat matriks A’ tetapi keduanya lebih kecil dari jumlah yang tidak diketahui pada sistem (3). Oleh karena itu, berdasarkan teorema Rouché-Frobenius kita mengetahui bahwa ini adalah sistem kompatibel tak tentu (ICS):

\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}

Latihan 3

Tentukan jenis sistem sistem persamaan berikut menggunakan teorema Rouché-Frobenius:

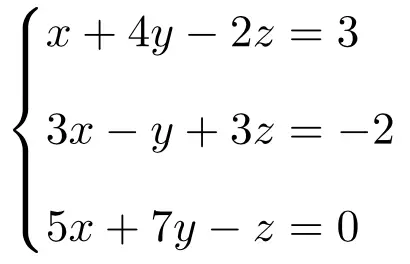
latihan diselesaikan langkah demi langkah teorema rouche - frobenius

Pertama-tama kita buat matriks A dan matriks perluasan A’ dari sistem:

\displaystyle A= \left( \begin{array}{ccc} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 4 & -2 & 3 \\[1.1ex] 3 & -1 & 3 & -2 \\[1.1ex] 5 & 7 & -1 & 0 \end{array} \right)

Sekarang mari kita hitung jangkauan matriks A:

\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1\end{vmatrix} = 0

\displaystyle \begin{vmatrix} 1 & 4 \\[1.1ex] 3 & -1 \end{vmatrix} = -13 \neq 0

Jadi matriks A mempunyai rangking 2:

\displaystyle rg(A)=2

Setelah kita mengetahui pangkat A, kita menghitung pangkat A’. Kita telah mengetahui bahwa determinan dari 3 kolom pertama menghasilkan 0, tetapi bukan determinan dari 3 kolom terakhir:

\displaystyle \begin{vmatrix} 4 & -2 & 3 \\[1.1ex]-1 & 3 & -2 \\[1.1ex] 7 & -1 & 0 \end{vmatrix} = -40 \neq 0

Oleh karena itu, matriks A’ mempunyai rangking 3 :

\displaystyle rg(A')=3

Pangkat matriks A lebih kecil dari pangkat matriks A’, oleh karena itu kita dapat menyimpulkan dari teorema Rouché-Frobenius bahwa ini merupakan Sistem Tidak Kompatibel (SI) :

\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}

Latihan 4

Tentukan jenis sistem persamaan berikut dengan 3 yang tidak diketahui menggunakan teorema Rouché-Frobenius:

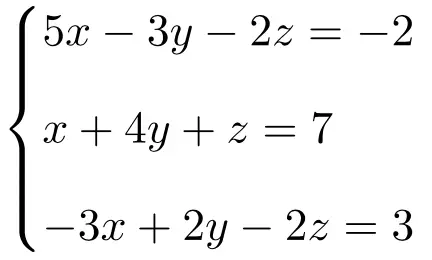
Rouche - Teorema Frobenius menyelesaikan latihan dengan 3 hal yang tidak diketahui dan 3 persamaan

Pertama-tama kita buat matriks A dan matriks perluasan A’ dari sistem:

\displaystyle A= \left( \begin{array}{ccc} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 5 & -3 & -2 & -2 \\[1.1ex] 1 & 4 & 1 & 7 \\[1.1ex]-3 & 2 & -2 & 3 \end{array} \right)

Sekarang kita harus menghitung rank matriks A. Untuk melakukannya, kita menyelesaikan determinan matriks dengan aturan Sarrus:

\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{vmatrix} = -40+9-4-24-10-6=-75 \bm{\neq 0}

Matriks yang mempunyai determinan orde ketiga selain 0, matriks A mempunyai rangking 3:

\displaystyle rg(A)=3

Oleh karena itu, matriks A’ juga mempunyai rangking 3 , karena matriks tersebut paling sedikit selalu mempunyai rangking A dan matriks tersebut tidak mungkin mempunyai rangking 4 karena kita tidak dapat menyelesaikan determinan 4×4 apa pun.

\displaystyle rg(A')=3

Jadi, berkat penerapan teorema Rouché-Frobenius, kita mengetahui bahwa sistem tersebut merupakan Sistem Penentuan Kompatibel (SCD), karena jangkauan A sama dengan jangkauan A’ dan jumlah yang tidak diketahui.

\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}

Latihan 5

Identifikasi jenis sistem sistem persamaan berikut menggunakan teorema Rouché-Frobenius:

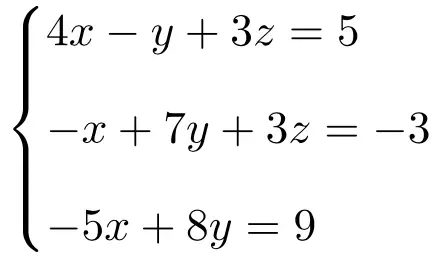
contoh teorema rouche - frobenius

Pertama-tama kita buat matriks A dan matriks perluasan A’ dari sistem:

\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 3 & 5 \\[1.1ex] -1 & 7 & 3 & -3 \\[1.1ex] -5 & 8 & 0 & 9 \end{array} \right)

Sekarang mari kita hitung jangkauan matriks A:

\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0\end{vmatrix} = 0

\displaystyle \begin{vmatrix} 4 & -1 \\[1.1ex] -1 & 7 \end{vmatrix} = 27 \neq 0

Oleh karena itu, matriks A berada pada peringkat 2:

\displaystyle rg(A)=2

Setelah kita mengetahui pangkat A, kita menghitung pangkat A’. Penentu 3 kolom pertama yang kita ketahui menghasilkan 0, tetapi determinan 3 kolom terakhir tidak memberikan:

\displaystyle \begin{vmatrix} -1 & 3 & 5 \\[1.1ex] 7 & 3 & -3 \\[1.1ex] 8 & 0 & 9\end{vmatrix} = -408 \neq 0

Oleh karena itu, matriks A’ mempunyai rangking 3 :

\displaystyle rg(A')=3

Dan terakhir, kita terapkan domain tersebut pada teorema Rouché-Frobenius: domain matriks A lebih kecil dari domain matriks A’, oleh karena itu merupakan Sistem Tidak Kompatibel (SI) :

\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}

Latihan 6

Klasifikasikan sistem persamaan orde 3 berikut dengan teorema Rouché-Frobenius:

\begin{cases} 6x-2y+4z=1 \\[1.5ex] -2x+4y+3z= 7 \\[1.5ex] 8x-6y+z = -6\end{cases}

Pertama-tama kita buat matriks A dan matriks perluasan A’ dari sistem:

\displaystyle A= \left( \begin{array}{ccc} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 6 & -2 & 4 & 1 \\[1.1ex] -2 & 4 & 3 & 7 \\[1.1ex] 8 & -6 & 1 & -6 \end{array} \right)

Sekarang mari kita hitung jangkauan matriks A:

\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{vmatrix} = 0

\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0

Jadi matriks A mempunyai rangking 2:

\displaystyle rg(A)=2

Setelah kita mengetahui pangkat A, kita menghitung pangkat A’. Kita sudah tahu bahwa determinan dari 3 kolom pertama menghasilkan 0, jadi kita coba kemungkinan determinan 3×3 lainnya:

\displaystyle \begin{vmatrix} -2 & 4 & 1 \\[1.1ex]4 & 3 & 7 \\[1.1ex] -6 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix}6 & 4 & 1 \\[1.1ex] -2 & 3 & 7 \\[1.1ex] 8 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix} 6 & -2 & 1 \\[1.1ex] -2 & 4 & 7 \\[1.1ex] 8 & -6 & -6\end{vmatrix} = 0

Semua determinan matriks A’ berukuran 3×3 adalah 0, sehingga matriks A’ juga tidak menduduki rangking 3. Namun di dalamnya memang terdapat determinan orde 2 yang berbeda dengan 0. Contoh:

\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0

Jadi matriks A’ akan mempunyai rangking 2 :

\displaystyle rg(A')=2

Terakhir, dengan menerapkan teorema Rouché-Frobenius, kita mengetahui bahwa ini adalah Sistem Kompatibel Tak tentu (ICS), karena jangkauan matriks A sama dengan jangkauan matriks A’ tetapi keduanya lebih kecil dari jumlah yang tidak diketahui di dalam sistem. sistem(3):

\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}

Tinggalkan Komentar

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *

Scroll to Top