Sudut antara dua garis (rumus)

Di halaman ini Anda akan menemukan penjelasan cara menghitung sudut antara dua garis (rumus). Anda juga akan dapat melihat beberapa contoh dan, sebagai tambahan, Anda akan dapat berlatih dengan latihan yang diselesaikan langkah demi langkah.

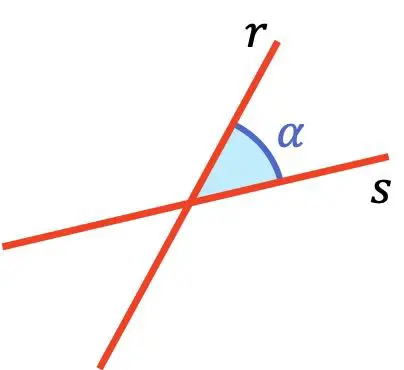
Berapakah sudut antara dua garis?

Sudut antara dua garis adalah sudut terkecil antara kedua garis tersebut.

Dalam denahnya terdapat empat jenis garis tergantung pada sudut yang terbentuk di antara keduanya: garis berpotongan (antara 0º dan 90º), garis tegak lurus (90º), garis sejajar (0º) dan garis berimpit (0º).

garis-garis yang berpotongan

Garis berpotongan berpotongan pada sudut lancip antara 0º dan 90º.

Garis lurus tegak lurus

Garis tegak lurus berpotongan membentuk sudut siku-siku 90º.

Garis sejajar

Garis sejajar tidak pernah bersentuhan dan membentuk sudut 0º di antara keduanya.

garis yang bertepatan

Dua garis yang berhimpitan mempunyai semua titik yang sama sehingga selalu ada sudut 0º di antara keduanya.

Kesimpulannya, perhitungan sudut antara dua garis sejajar, berimpit, atau tegak lurus adalah langsung: garis sejajar dan garis berimpit membentuk sudut 0 derajat karena arahnya sama, dan garis tegak lurus tersebut berpotongan dengan sudut 90 derajat. . Sebaliknya, untuk mencari sudut antara dua garis yang berpotongan, Anda harus menerapkan rumus (kita akan melihatnya di bawah).

Bagaimana cara menghitung sudut antara dua garis?

Ada dua cara untuk menghitung sudut antara dua garis. Cara pertama menggunakan vektor arah setiap garis dan cara kedua berdasarkan kemiringan setiap garis.

Tidak ada prosedur yang lebih baik dari yang lain, pada kenyataannya keduanya cukup mudah, namun bergantung pada bagaimana garis-garis tersebut diungkapkan, satu metode atau lainnya praktis. Oleh karena itu kami menyarankan Anda mengetahui cara menggunakan kedua metode matematika tersebut.

Metode orientasi vektor garis

Rumus menghitung sudut antara dua garis dengan menggunakan vektor arahnya adalah:

Diketahui vektor arah dari dua garis yang berbeda:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)\qquad \vv{\text{v}} = (\text{v}_x,\text{v}_y)$

Sudut antara kedua garis tersebut dapat dihitung dengan rumus berikut:

$\displaystyle \cos(\alpha) =\cfrac{\lvert \vv{\text{u}} \cdot \vv{\text{v}}\rvert}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert}$

Emas

$\lvert \vv{\text{u}} \rvert$

Dan

$\lvert \vv{\text{v}} \rvert$

adalah modul dari vektor

$\vv{\text{u}}$

Dan

$\vv{\text{v}}$

masing-masing.

Ingatlah bahwa rumus besar suatu vektor adalah:

$\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{ \text{v}_x^2+\text{v}_y^2}$

Mari kita lihat cara mencari sudut antara dua garis dengan contoh:

Hitunglah sudut antara dua garis berikut:

$\displaystyle r: \ \begin{cases} x=2-3t \\[2ex]y=1+4t \end{cases} \qquad s: \ 2x-5y+7=0$

Untuk menghitung sudut antara dua garis, Anda harus terlebih dahulu mencari vektor arah setiap garis.

hak

$r$

dinyatakan dalam bentuk persamaan parametrik , maka komponen vektor yang menandai arahnya adalah:

$\vv{r} = (-3,4)$

dan hukum

$\displaystyle s$

didefinisikan dalam bentuk persamaan implisit (atau umum), sehingga koordinat vektor arahnya adalah:

$\vv{s} = (-B,A)$

$\vv{s} = (5,2)$

Sekarang setelah kita mengetahui vektor arah setiap garis, kita dapat menggunakan rumus sudut antara dua garis:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

Oleh karena itu kita tentukan besar kedua vektor tersebut:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{(-3)^2+4^2}= 5$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{5^2+2^2}= \sqrt{29}$

Kami melakukan operasi vektor dari rumus sudut:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(-3,4) \cdot (5,2)\rvert}{5 \cdot \sqrt{29}}= \cfrac{\lvert-3 \cdot 5 + 4\cdot 2\rvert}{26,93} = \cfrac{7}{26,93} = 0,26$

Dan terakhir, kita menghitung sudut yang dibentuk oleh dua garis dengan kebalikan kosinus:

$\alpha= \text{cos}^{-1}(0,26) = \bm{74,93º}$

Ingatlah bahwa Anda dapat menghitung invers kosinus menggunakan kalkulator dengan kuncinya

$\boxed{\cos ^{-1}}.$

metode kemiringan

Tentunya untuk memahami cara ini, Anda perlu mengetahui kemiringan garis . Anda dapat meninjau konsep ini di tautan, di mana Anda akan menemukan penjelasan rinci tentang artinya, cara menghitungnya, contoh dan latihan penyelesaian kemiringan suatu garis.

Rumus menghitung sudut antara dua garis dari lerengnya adalah:

Atau dua baris berbeda:

$r_1 : \ y=m_1 x+n_1 \qquad r_2: \ y=m_2 x+n_2$

Sudut antara kedua garis tersebut dapat ditentukan dengan rumus berikut:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_2-m_1}{1+m_1\cdot m_2} \end{vmatrix}$

Emas

$m_1$

Dan

$m_2$

adalah kemiringan garis

$r_1$

Dan

$r_2$

masing-masing.

Mari kita lihat cara menghitung sudut antara dua garis menggunakan kemiringannya dengan contoh:

Tentukan sudut antara dua garis berikut:

$\displaystyle r: \ y=4x-2 \qquad s: \ y=-3x+1$

Kemiringan setiap garis adalah angka sebelum variabel

$x:$

$m_r = 4$

$m_s = -3$

Oleh karena itu, sudut antara dua garis dapat dicari dengan menggunakan rumus kemiringan:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{-3-4}{1+4\cdot (-3)} \end{vmatrix}=\begin{vmatrix} \cfrac{-7}{-11} \end{vmatrix} = 0,64$

Dan akhirnya kita menemukan sudut dengan kebalikan dari garis singgung:

$\alpha= \text{tg}^{-1}(0,64) = \bm{32,62º}$

Ingatlah bahwa Anda dapat menghitung kebalikan dari garis singgung menggunakan kalkulator dengan kuncinya

$\boxed{\tan ^{-1}}.$

Kita baru saja melihat contoh kemiringan dua garis yang dinyatakan sebagai persamaan eksplisit, namun jika keduanya berbentuk persamaan kemiringan titik, prosedur yang sama harus digunakan.

Menyelesaikan masalah sudut antara dua garis

Latihan 1

Tentukan sudut yang dibentuk oleh dua garis berikut:

$\displaystyle r: \ \begin{cases} x=4+t \\[2ex]y=-3-2t \end{cases} \qquad s: \ \begin{cases} x=4t \\[2ex]y=-1-t \end{cases}$

lihat solusi

Dalam hal ini kita akan menggunakan metode vektor arah. Oleh karena itu, kita harus mencari terlebih dahulu vektor arah setiap garis. Kedua garis tersebut dinyatakan sebagai persamaan parametrik, sehingga komponen vektor arahnya adalah suku di depan parameternya

$t:$

$\vv{r} = (1,-2)$

$\vv{s} = (4,-1)$

Sekarang setelah kita mengetahui vektor arah setiap garis, kita dapat menggunakan rumus sudut antara dua garis:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

Oleh karena itu kita tentukan besar kedua vektor tersebut:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{1^2+(-2)^2}= \sqrt{5}$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{4^2+(-1)^2}= \sqrt{17}$

Kami menyelesaikan produk skalar antara dua vektor pembilang dan perkalian modul penyebut:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(1,-2) \cdot (4,-1)\rvert}{\sqrt{5} \cdot \sqrt{17}}= \cfrac{\lvert 1 \cdot 4 + (-2)\cdot (-1)\rvert}{9,22} = \cfrac{6}{9,22} = 0,65$

Dan terakhir, kita mencari sudut yang dibentuk oleh dua garis dengan melakukan invers kosinus:

$\alpha= \text{cos}^{-1}(0,65) = \bm{49,40º}$

Latihan 2

Tentukan sudut antara dua garis berikut:

$\displaystyle r: \ -3x+4y+1=0 \qquad s: \ \cfrac{x-1}{6} = \cfrac{y+5}{3}$

lihat solusi

Kita akan menyelesaikan soal ini dengan menggunakan metode vektor arah, jadi pertama-tama kita perlu mencari vektor arah setiap garis. hak

$r$

dinyatakan dalam bentuk persamaan umum (atau implisit), sehingga komponen vektor yang menandai arahnya adalah:

$\vv{r} = (-B,A)$

$\vv{r} = (-4,-3)$

dan hukum

$\displaystyle s$

didefinisikan dalam bentuk persamaan kontinu, sehingga koordinat kartesius vektor arahnya adalah bilangan penyebutnya:

$\vv{s} = (6,3)$

Setelah kita mengetahui vektor arah setiap garis, kita dapat menggunakan rumus sudut antara dua garis:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

Oleh karena itu kami menentukan modul dari dua vektor:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{(-4)^2+(-3)^2}= 5$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{6^2+3^2}= \sqrt{45}$

Kami melakukan operasi antar vektor dengan rumus sudut:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(-4,-3) \cdot (6,3)\rvert}{5 \cdot \sqrt{45}}= \cfrac{\lvert -4 \cdot 6 + (-3)\cdot 3\rvert}{33,54} = \cfrac{33}{33,54} = 0,98$

Dan terakhir, kita menghitung sudut yang dibentuk oleh dua garis dengan kebalikan kosinus:

$\alpha= \text{cos}^{-1}(0,98) = \bm{10,30º}$

Latihan 3

Berapakah sudut antara dua garis berikut?

$\displaystyle r: \ y=-2x+9 \qquad s: \ y=5x-1$

lihat solusi

Dalam hal ini, kita akan menggunakan metode kemiringan garis untuk mengetahui sudut yang dibentuknya, karena garis-garis tersebut berbentuk persamaan eksplisit.

Kemiringan setiap garis merupakan bilangan yang menyertai variabel bebas

$x:$

$m_r = -2$

$m_s = 5$

Oleh karena itu, sudut antara kedua garis dapat ditentukan dengan menggunakan rumus kemiringan:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{-2-5}{1+5\cdot (-2)} \end{vmatrix}=\begin{vmatrix} \cfrac{-7}{-9} \end{vmatrix} = 0,78$

Dan terakhir kita mencari sudut antara dua garis dengan membalik garis singgungnya:

$\alpha= \text{tg}^{-1}(0,78) = \bm{37,87º}$

Latihan 4

Temukan persamaan garis yang melalui titik tersebut

$P(5,-1)$

dan membentuk sudut 45º dengan garis

$r.$

Dikatakan baris:

$\displaystyle r: \ y=2x+4$

lihat solusi

Untuk mengatasi masalah ini, kami akan menelepon

$s$

ke kanan yang akan kita hitung. Selain itu, kita akan menggunakan metode kemiringan karena kita mengetahui kemiringan garis

$r:$

$m_r=2$

Dari rumus sudut antara dua garis (metode kemiringan) kita dapat memperoleh nilai kemiringan garis

$s:$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

Kami mengganti nilai yang diketahui ke dalam rumus:

$\displaystyle \text{tg}(45º) =\begin{vmatrix} \cfrac{m_s-2}{1+2\cdot m_s} \end{vmatrix}$

Dan kami mencoba menyelesaikan persamaan yang dihasilkan:

$\displaystyle 1 =\begin{vmatrix} \cfrac{m_s-2}{1+2m_s} \end{vmatrix}$

Nilai absolut persamaan membuatnya agak sulit untuk diselesaikan, karena Anda harus menganalisis opsi positif dan negatif:

$\displaystyle 1 =+\cfrac{m_s-2}{1+2m_s}$

$\displaystyle 1 \cdot (1+2m_s)=m_s-2$

$\displaystyle 1+2m_s=m_s-2$

$\displaystyle 2m_s-m_s=-2-1$

$\displaystyle m_s=-3$

$\displaystyle 1 =-\cfrac{m_s-2}{1+2m_s}$

$\displaystyle 1 \cdot (1+2m_s)=-(m_s-2)$

$\displaystyle 1+2m_s=-m_s+2$

$\displaystyle 2m_s+m_s=2-1$

$\displaystyle 3m_s=1$

$\displaystyle m_s=\cfrac{1}{3}$

Oleh karena itu kita mempunyai dua kemungkinan solusi: sebuah garis dengan kemiringan -3 dan garis lainnya dengan kemiringan sepertiga.

Rumus persamaan titik-kemiringan suatu garis adalah:

$y-y_0=m(x-x_0)$

Oleh karena itu, setelah kita mengetahui kemiringan kedua garis yang mungkin terjadi, kita dapat menuliskan persamaan titik-kemiringan setiap garis dengan titik yang harus dilaluinya sesuai dengan pernyataan,

$P(5,-1):$

$\displaystyle s: \ y+1=-3(x-5) \qquad \qquad s': \ y+1=\cfrac{1}{3}(x-5)$

Berapakah sudut antara dua garis?

Bagaimana cara menghitung sudut antara dua garis?

Metode orientasi vektor garis

metode kemiringan

Menyelesaikan masalah sudut antara dua garis

Latihan 1

Latihan 2

Latihan 3

Latihan 4

Tinggalkan Komentar Batalkan Balasan