Sistem persamaan adalah himpunan dua persamaan atau lebih yang mempunyai lebih dari satu persamaan yang tidak diketahui. Jadi, untuk menyelesaikan sistem, kita dapat menggunakan empat metode: substitusi, pemerataan, reduksi, dan grafik. Namun, sebelum mulai menjelaskan prosedur solusi, kami akan mendefinisikan jenis sistem yang ada menurut jumlah solusinya:
- Sistem kompatibel yang ditentukan: hanya mempunyai satu solusi dan dapat diwakili oleh dua garis yang berpotongan pada satu titik (yang merupakan solusi).
- Sistem kompatibel tak tentu: sistem ini mempunyai solusi tak terhingga, hal ini disebabkan oleh adanya dua garis yang berimpit pada titik yang sama.
- Sistem yang tidak kompatibel: tidak memiliki solusi, karena garis-garisnya sejajar sehingga tidak memiliki titik yang sama.
Metode penyelesaian sistem persamaan linear
Sekarang kami akan menjelaskan berbagai sistem yang dapat kita gunakan untuk menyelesaikan sistem persamaan. Dalam penjelasannya Anda akan menemukan teori dan beberapa contoh, sehingga semua konsep yang dijelaskan menjadi lebih jelas. Perhatikan bahwa dalam artikel ini kita hanya akan membahas tentang sistem persamaan 2×2 , artinya kita hanya akan membahas sistem yang terdiri dari dua persamaan. Karena itu, mari kita mulai dengan penjelasannya.
metode substitusi
Metode substitusi terdiri dari mengisolasi salah satu yang tidak diketahui dalam salah satu persamaan dan kemudian mensubstitusi ekspresi yang diperoleh ke dalam persamaan sebaliknya. Metode ini paling direkomendasikan ketika setidaknya salah satu dari yang tidak diketahui memiliki nilai koefisien sama dengan 1. Jadi, langkah-langkah yang harus diikuti sangat sederhana:
- Pisahkan kuantitas yang tidak diketahui dari salah satu dari dua persamaan.
- Substitusikan ke dalam persamaan lain persamaan yang ekuivalen dengan persamaan yang tidak diketahui yang telah kita hilangkan dari persamaan pertama.
- Hapus kebalikan yang tidak diketahui dalam persamaan yang kita peroleh.
- Setelah kita mendapatkan nilai variabel pertama, kita perlu menggunakannya untuk mencari nilai variabel kedua.
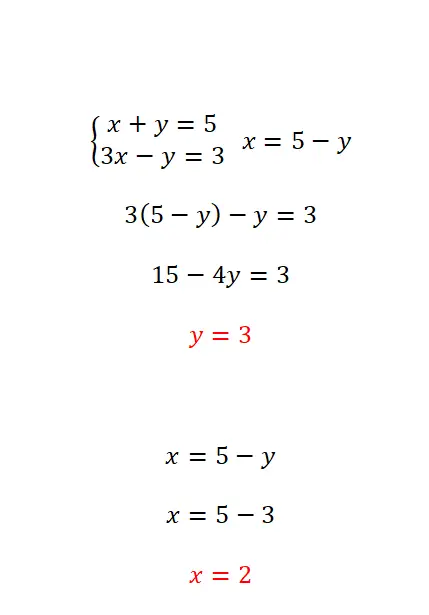
metode pemerataan
Metode pencocokan terdiri dari mengisolasi variabel yang sama dalam dua persamaan kemudian mencocokkan dua ekspresi yang diperoleh. Metode ini direkomendasikan jika hal yang tidak diketahui dapat dengan mudah diisolasi di kedua persamaan, karena akan mempermudah seluruh perhitungan. Prosedur yang harus Anda ikuti dalam hal ini adalah sebagai berikut:
- Kami mengisolasi hal yang tidak diketahui yang telah kami pilih dalam dua persamaan.
- Kami mengasimilasi ekspresi yang setara dengan hal yang tidak diketahui ini.
- Kami menyelesaikan persamaan secara normal.
- Kami menghitung yang tidak diketahui lainnya dengan nilai yang kami hitung.
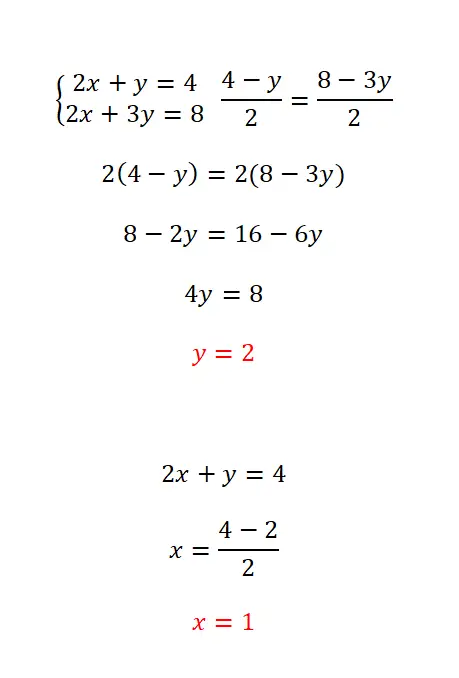
metode reduksi
Metode reduksi didasarkan pada mengalikan kedua persamaan dengan dua angka, yang memungkinkan kita memperoleh koefisien yang sama dengan tanda yang berbeda dari salah satu variabel di kedua ekspresi. Metode ini paling direkomendasikan jika variabel yang tidak diketahui memiliki koefisien yang sama di semua persamaan atau jika koefisien yang berlawanan tandanya sama. Dan tata cara penyelesaiannya adalah sebagai berikut:
- Kedua persamaan tersebut dikalikan dengan angka-angka yang diperlukan (Anda harus menemukan dua angka yang memungkinkan diperolehnya koefisien yang sama untuk salah satu dari dua variabel dalam dua persamaan, tetapi bertanda berlawanan).
- Kemudian persamaan tersebut dikurangkan atau dijumlahkan untuk menghilangkan hal yang tidak diketahui tersebut dengan koefisiennya masing-masing.
- Kemudian persamaan sisanya diselesaikan.
- Dan kami menggunakan hasil persamaan ini untuk mendapatkan nilai numerik yang kami lewatkan pada variabel lainnya.
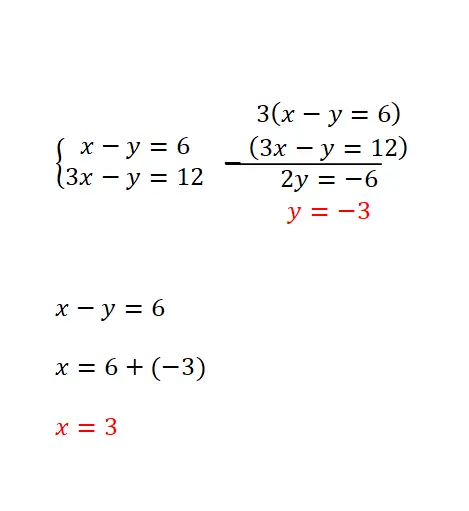
metode grafis
Terakhir, kita dapat memilih untuk menyelesaikan sistem persamaan melalui representasi grafis . Metode ini sangat berbeda dari metode lainnya, karena metode ini tidak memiliki bagian matematis yang rumit, melainkan hampir seluruhnya bersifat grafis. Jadi, untuk mengetahui nilai-nilai yang tidak diketahui, kita harus menyusun kedua persamaan tersebut dalam bentuk persamaan garis: y = mx + b . Dengan cara ini kita akan dapat membuat representasinya, kita akan mengasosiasikan nilai koordinat titik potong antara kedua fungsi tersebut dengan yang tidak diketahui. Berikut adalah contoh yang berhasil:
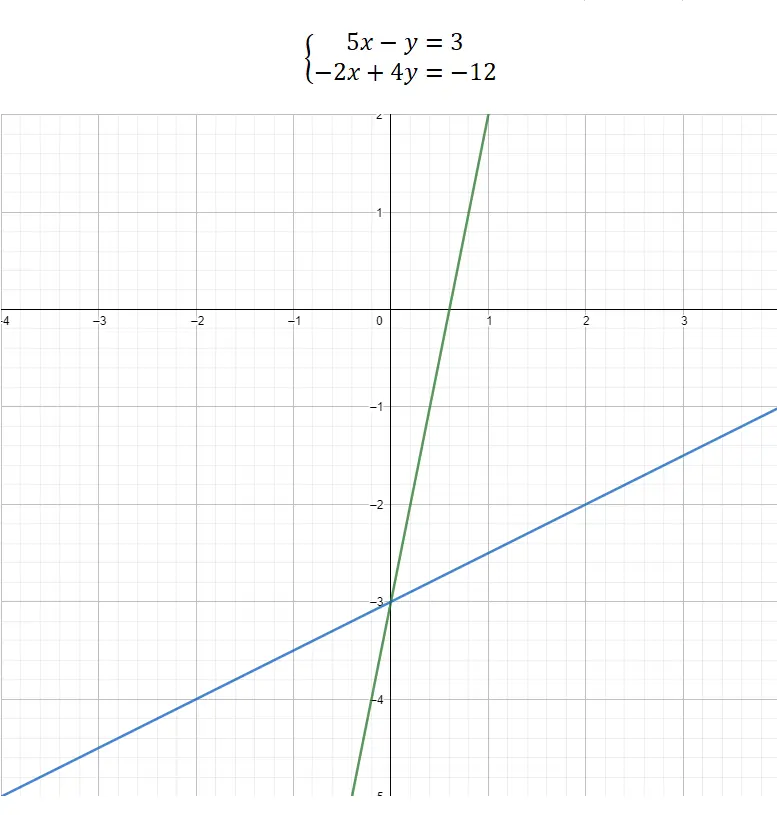
Terlihat pada grafik, titik potong antara kedua fungsi tersebut adalah (0, -3). Jadi nilai x = 0 dan nilai y = -3. Beginilah cara sistem persamaan diselesaikan secara grafis.
Bagaimana cara menyelesaikan sistem persamaan kuadrat?
Untuk menyelesaikan sistem persamaan kuadrat, kita dapat menggunakan metode yang baru saja kita bahas. Secara pribadi, kami merekomendasikan metode substitusi karena metode ini memungkinkan kita memperoleh persamaan dengan satu persamaan yang tidak diketahui dengan cepat. Sebaliknya jika kita menggunakan metode reduksi atau pemerataan maka perhitungannya menjadi cukup rumit. Jadi, setelah Anda mensubstitusi salah satu dari kedua variabel tersebut, Anda hanya perlu menyelesaikan persamaan kuadrat atau persamaan kuadrat yang dihasilkan. Berikut ini contohnya sehingga Anda dapat melihat keseluruhan prosesnya:
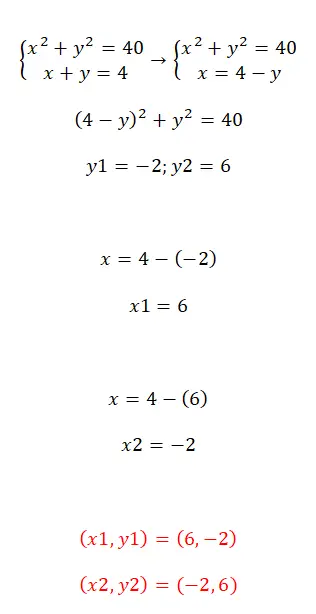
Latihan memecahkan sistem persamaan
Kami sekarang menawarkan kepada Anda beberapa latihan tentang sistem persamaan linier dan kuadrat sehingga Anda dapat menerapkan teori yang dijelaskan. Dengan cara ini Anda akan lebih memahami semua konsep yang berkaitan dengan sistem persamaan penghitungan. Kami menyarankan Anda mencoba menyelesaikannya sebelum melihat jawaban yang kami tawarkan, dengan cara ini Anda akan mendapatkan hasil maksimal dari latihan:
Latihan 1
Selesaikan sistem persamaan ini dengan menggunakan metode substitusi:
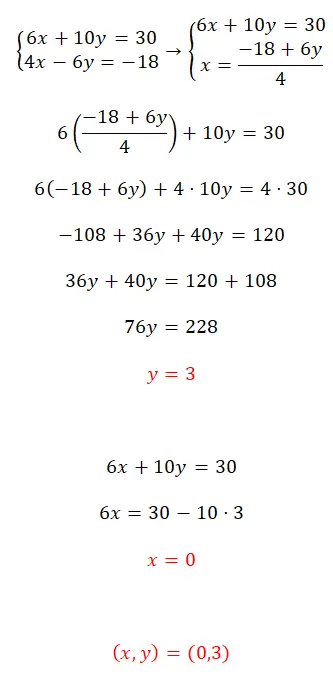
- Kita mulai dengan mengisolasi salah satu dari dua hal yang tidak diketahui dalam sebuah persamaan.
- Kemudian kita substitusikan ekspresi yang diperoleh dalam persamaan sebaliknya, dengan persamaan yang tidak diketahui yang telah kita selesaikan sebelumnya.
- Kami kemudian memperoleh hasil dari variabel sebaliknya.
- Selanjutnya, kita substitusikan nilai pertama yang ditemukan ke dalam salah satu dari dua persamaan untuk menghitung nilai nilai pertama yang tidak diketahui.
- Terakhir, kami menyatakan hasil dari kedua variabel tersebut.
Latihan 2
Selesaikan sistem persamaan ini dengan menggunakan metode substitusi:
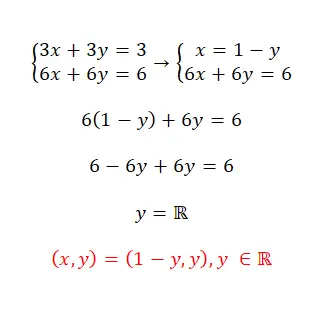
- Dalam hal ini kita akan mengikuti prosedur yang sama: mengisolasi variabel yang tidak diketahui, menggantinya dengan ekspresi lain, dan mengisolasi variabel kedua.
- Seperti yang bisa kita lihat, ini adalah sistem kompatibel yang tidak dapat ditentukan, karena mempunyai banyak sekali solusi.
Latihan 3
Selesaikan sistem persamaan ini menggunakan metode pemerataan:
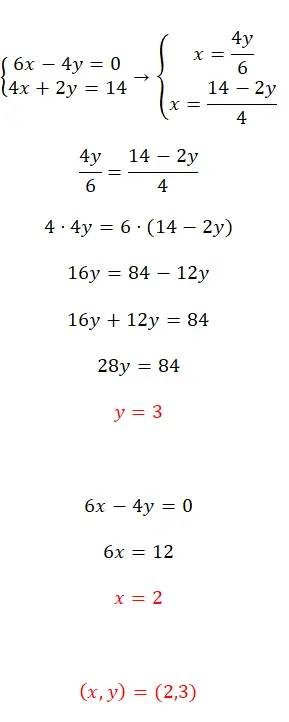
- Langkah pertama adalah mengisolasi variabel yang sama di kedua persamaan, dalam hal ini kita memilih x.
- Kemudian kami mencocokkan ekspresi yang dihasilkan dan mulai menyelesaikannya.
- Jadi, kita memperoleh nilai yang tidak diketahui pertama.
- Dan jika kita mensubstitusikannya ke salah satu dari dua persamaan awal, kita dapat menghitung persamaan kedua yang tidak diketahui.
- Terakhir, kami menyatakan hasil dari kedua variabel tersebut.
Latihan 4
Selesaikan sistem persamaan ini menggunakan metode pemerataan:
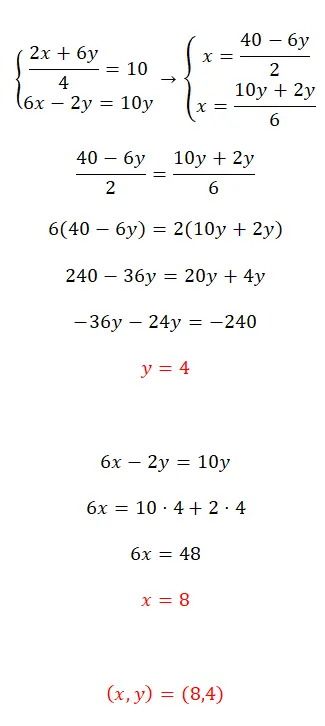
- Pertama, kita isolasi x pada kedua persamaan.
- Selanjutnya, kita mencocokkan ekspresi yang kita peroleh.
- Kami memperoleh nilai yang tidak diketahui pertama.
- Kami mengganti nilai ini ke dalam salah satu dari dua persamaan awal dan menghitung persamaan kedua yang tidak diketahui.
- Terakhir, kami mengungkapkan nilai dari dua orang asing tersebut.
Latihan 5
Selesaikan sistem persamaan ini dengan menggunakan metode reduksi:
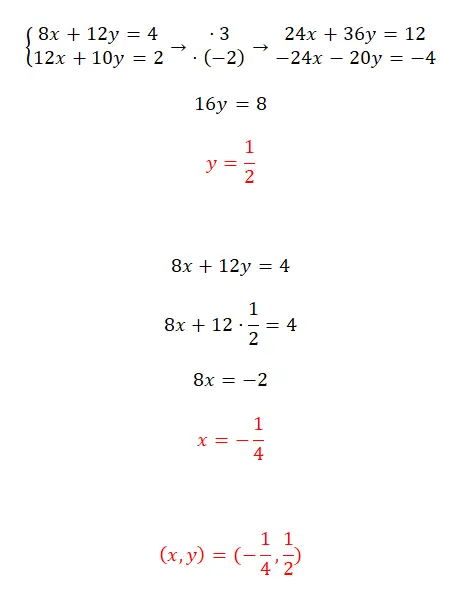
- Anda harus mencari dua bilangan yang memungkinkan diperolehnya koefisien yang sama untuk salah satu dari dua variabel dalam dua persamaan, tetapi bertanda berlawanan .
- Kemudian, selesaikan saja persamaan yang kita peroleh dengan menjumlahkan dua ekspresi yang diperoleh.
- Selanjutnya, kita substitusikan y ke dalam salah satu dari dua persamaan awal, untuk menghitung x.
- Terakhir, kami mengungkapkan hasil dari sistem.
Latihan 6
Selesaikan sistem persamaan ini dengan menggunakan metode reduksi:
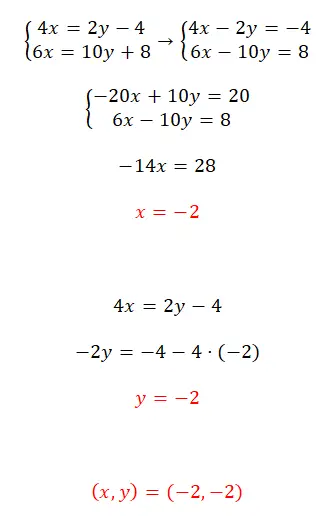
- Kita mulai dengan menyusun persamaan (melewati semua variabel ke kiri).
- Lalu kita kalikan persamaan pertama dengan -5.
- Kita selesaikan persamaan yang kita peroleh dengan menjumlahkan kedua persamaan tersebut dan memperoleh nilai x.
- Kami menggunakan nilai yang diketahui ini untuk mendapatkan nilai y.
- Kami menyatakan hasil dari sistem persamaan.
Latihan 7
Selesaikan sistem persamaan ini dengan menggunakan metode substitusi:
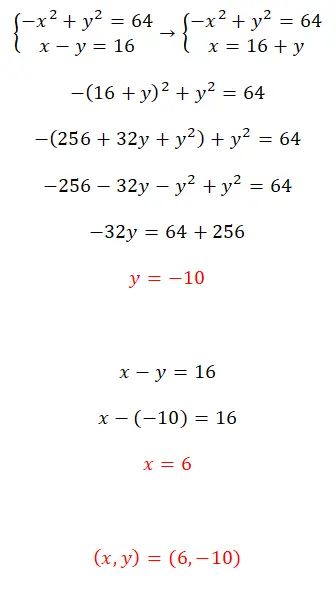
- Untuk menyelesaikan sistem persamaan nonlinier ini, sebaiknya gunakan metode substitusi.
- Jadi, Anda membuat persamaan dengan ekspresi yang setara dengan x.
- Anda mendapatkan nilai y yang tidak diketahui.
- Anda menghitung nilai x dengan nilai yang Anda hitung sebelumnya.
- Dan Anda sudah memiliki kedua nilai tersebut.
Latihan 8
Selesaikan sistem persamaan ini menggunakan metode pilihan Anda:
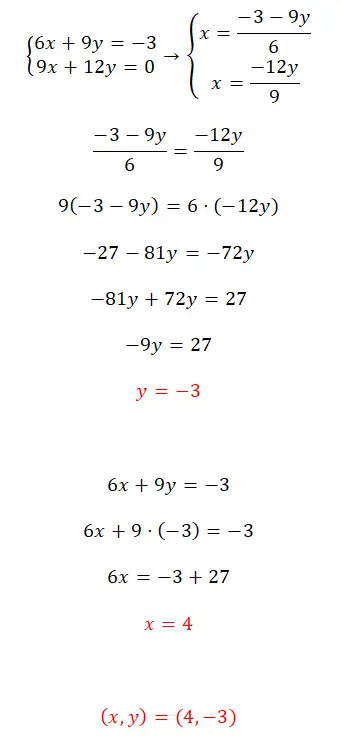
- Dalam hal ini, kami disajikan dengan sistem kompatibel yang ditentukan dan kami akan menyelesaikannya menggunakan metode pemerataan.
- Oleh karena itu, kita menyelesaikan x pada kedua persamaan dan menyamakan kedua ekspresi yang dihasilkan.
- Setelah menyelesaikan persamaan tersebut, kita mendapatkan nilai y.
- Kami menggunakan nilai ini untuk mencari nilai x.
- Terakhir, kami mengungkapkan hasil dari sistem.