Bilangan kombinatorial (atau koefisien binomial)

Pada halaman ini kami menjelaskan apa itu bilangan kombinatorial dan cara menghitungnya (rumus). Selain itu, Anda akan dapat melihat contoh cara menghitung bilangan kombinatorial dan berlatih dengan latihan yang diselesaikan langkah demi langkah. Kami juga menunjukkan semua properti dan penerapan bilangan kombinatorial. Dan terakhir, kita belajar mencari hasil bilangan kombinatorial langsung dengan kalkulator.

Apa itu bilangan kombinatorial?

Dalam matematika, bilangan kombinatorial , disebut juga koefisien binomial, adalah banyaknya kombinasi biasa (kombinasi tanpa pengulangan) kelompok k elemen yang dapat dibentuk dari himpunan n elemen (n>k).

Bilangan kombinatorial dinyatakan dalam tanda kurung sebagai berikut:

\begin{pmatrix}n \\ k \end{pmatrix}

Sebaliknya, bilangan kombinatorial dibaca n di atas k . Demikian pula, n disebut pembilang dan k disebut ordo.

Hanya dengan definisi bilangan kombinatorial saja sudah sulit untuk memahami maknanya. Namun, sekarang kita akan melihat bagaimana bilangan kombinatorik ditentukan secara matematis, dan kemudian kita akan mempelajari lebih dalam konsep kombinatorik ini. Anda akan melihat bahwa dengan cara ini Anda akan memahaminya dengan lebih baik.

Rumus bilangan kombinatorial

Rumus untuk menghitung nilai suatu bilangan kombinatorial (atau koefisien binomial) adalah sebagai berikut:

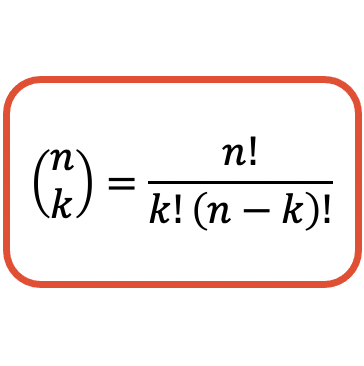
rumus bilangan kombinatorial

Ingatlah bahwa dalam aljabar, tanda seru sama dengan faktorial suatu bilangan. Dan untuk mencari faktorial suatu bilangan, Anda perlu mengalikan semua bilangan bulat positif 1 dengan bilangan tersebut. Misalnya untuk menghitung faktorial bilangan 4 Anda harus mengalikan 1, 2, 3 dan 4:

4! = 1\cdot 2 \cdot 3 \cdot 4 =24

Penting juga untuk mengetahui bahwa faktorial dari 0 sama dengan 1.

0! = 1

Contoh penghitungan bilangan kombinatorial

Selanjutnya kita akan menentukan nilai suatu bilangan kombinatorial selangkah demi selangkah sebagai contoh, sehingga Anda dapat melihat cara kerjanya:

  • Hitung nilai bilangan kombinatorial 5 per 3.

Koefisien binomial 5 per 3 sesuai dengan ekspresi berikut:

\begin{pmatrix}5 \\ 3 \end{pmatrix}

Oleh karena itu, jika kita menerapkan rumus bilangan kombinatorial, untuk menentukan nilainya kita harus melakukan operasi berikut:

\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{5!}{3!(5-3)!}

Atau setara:

\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{5!}{3!\cdot 2!}

Oleh karena itu kami menemukan faktorialnya:

\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{1\cdot 2 \cdot 3 \cdot 4 \cdot 5}{(1\cdot 2 \cdot 3) \cdot (1\cdot 2)}

Perkalian 1·2·3 diulang pada pembilang dan penyebutnya, sehingga pecahan dapat disederhanakan dengan menghilangkan faktor berikut:

\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{\cancel{1\cdot 2 \cdot 3} \cdot 4 \cdot 5}{(\cancel{1\cdot 2 \cdot 3)} \cdot (1\cdot 2)}

\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{ 4 \cdot 5}{1\cdot 2}

Sekarang kita menghitung produknya:

\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{20}{2}

Dan terakhir kita buat pembagiannya:

\begin{pmatrix}5 \\ 3 \end{pmatrix} = \bm{10}

Sifat-sifat bilangan kombinatorial

Bilangan kombinatorial, atau koefisien binomial, dapat digabungkan menurut sifat-sifat berikut:

  • Dua bilangan kombinatorial yang saling melengkapi adalah bilangan yang mempunyai pembilang n yang sama dan jumlah ordonya ekuivalen dengan pembilangnya. Jadi, hasil dua bilangan kombinatorial komplementer adalah identik.

\begin{pmatrix}n \\ k \end{pmatrix} = \begin{pmatrix}n \\ n-k \end{pmatrix}

Ciri-ciri bilangan kombinatorial ini disebut juga identitas simetri.

Misalnya, 6 per 4 memberikan hasil yang sama dengan 6 per 2, karena 6-4=2.

\begin{pmatrix}6 \\ 4 \end{pmatrix} =\cfrac{6!}{4!(6-4)!} = \cfrac{\cancel{1\cdot 2 \cdot 3\cdot 4}\cdot 5 \cdot 6}{(\cancel{1\cdot 2 \cdot 3\cdot 4})\cdot (1\cdot 2)}= \cfrac{30}{2} = \bm{15}

\begin{pmatrix}6 \\ 2 \end{pmatrix} =\cfrac{6!}{2!(6-2)!} = \cfrac{\cancel{1\cdot 2 \cdot 3\cdot 4}\cdot 5 \cdot 6}{(1\cdot 2)\cdot (\cancel{1\cdot 2 \cdot 3\cdot 4})}= \cfrac{30}{2} = \bm{15}

  • Jumlah dua bilangan kombinatorial yang pembilangnya sama dan ordo-ordo berurutannya sama dengan bilangan kombinatorial lain yang pembilangnya setara dengan pembilang penjumlahan ditambah 1 dan ordonya sesuai dengan nilai terbesar ordo penjumlahan tersebut. Dengan kata lain, kondisi berikut selalu terpenuhi:

\begin{pmatrix}n\\ k \end{pmatrix} + \begin{pmatrix}n\\ k+1 \end{pmatrix}= \begin{pmatrix}n+1\\ k+1 \end{pmatrix}

Misalnya:

\begin{pmatrix}9\\ 2 \end{pmatrix} + \begin{pmatrix}9\\ 3 \end{pmatrix}= \begin{pmatrix}10\\ 3 \end{pmatrix}

Properti ini juga dikenal sebagai aturan Pascal.

Di sisi lain, rumus ini juga dapat diterapkan secara terbalik untuk menguraikan suatu bilangan kombinatorial menjadi dua bilangan kombinatorial yang lebih sederhana:

\begin{pmatrix}n\\ k \end{pmatrix} = \begin{pmatrix}n-1\\ k-1 \end{pmatrix}+ \begin{pmatrix}n-1\\ k \end{pmatrix}

Misalnya, bilangan kombinatorial 8 atas 4 sama dengan 7 atas 3 ditambah 7 atas 4:

\begin{pmatrix}8\\ 4 \end{pmatrix} = \begin{pmatrix}7\\ 3 \end{pmatrix}+ \begin{pmatrix}7\\ 4 \end{pmatrix}

  • Setiap bilangan positif yang lebih besar dari 1 sama dengan bilangan itu sendiri.

\begin{pmatrix}n\\ 1 \end{pmatrix} =n

Alasan sifat ini adalah faktorial suatu bilangan sama dengan faktorial bilangan sebelumnya dikalikan dengan bilangan itu sendiri:

\begin{pmatrix}n \\ 1 \end{pmatrix} =\cfrac{n!}{1!(n-1)!} = \cfrac{n\cdot (n-1) \cdot (n-2)\cdots 1}{(n-1) \cdot (n-2)\cdots 1}= n

Contoh bilangan kombinatorial jenis ini:

\begin{pmatrix}12\\ 1 \end{pmatrix} =12 \qquad \begin{pmatrix}5\\ 1 \end{pmatrix} =5 \qquad \begin{pmatrix}9\\ 1 \end{pmatrix} =9

  • Setiap bilangan positif yang lebih besar dari 0 sama dengan satu.

\begin{pmatrix}n\\ 0 \end{pmatrix} =1

Memang, penyebut pecahan dari bilangan kombinatorial tersebut akan selalu sama dengan pembilang pecahan:

\begin{pmatrix}n\\ 0 \end{pmatrix} =\cfrac{n!}{0!(n-0)!} =\cfrac{n!}{n!} = 1

Contoh bilangan kombinatorial seperti ini:

\begin{pmatrix}6\\ 0 \end{pmatrix} =1 \qquad \begin{pmatrix}2\\ 0 \end{pmatrix} =1 \qquad \begin{pmatrix}23\\ 0 \end{pmatrix} =1

  • Setiap angka itu sendiri sama dengan 1.

\begin{pmatrix}n\\ n \end{pmatrix} =1

Ini demonya:

\begin{pmatrix}n\\ n \end{pmatrix} =\cfrac{n!}{n!(n-n)!} =\cfrac{n!}{n!\cdot 0!}= \cfrac{n!}{n!} = 1

Contoh bilangan kombinatorial seperti ini:

\begin{pmatrix}5\\ 5 \end{pmatrix} =1 \qquad \begin{pmatrix}37\\ 37 \end{pmatrix} =1 \qquad \begin{pmatrix}14\\ 14 \end{pmatrix} =1

Cara menghitung bilangan kombinatorial dengan kalkulator

Selama ini kita telah melihat cara mencari bilangan kombinatorial dari bilangan yang kurang lebih sederhana, namun bila kita harus mengoperasikan besaran yang sangat besar ada baiknya menggunakan kalkulator untuk menentukan bilangan kombinatorial tersebut. Sekarang kita akan melihat cara memasukkan bilangan kombinatorial ke dalam kalkulator.

Jadi, kunci yang digunakan untuk menghitung suatu bilangan kombinatorial dengan kalkulator adalah kunci nCr . Dan untuk menentukan nilai bilangan kombinatorialnya, pertama-tama harus memasukkan pembilang dari bilangan kombinatorial tersebut, kedua tekan tombol nCr, kemudian masukkan urutan bilangan kombinatorialnya dan terakhir tekan tombol sama dengan.

\begin{pmatrix}n\\ k \end{pmatrix}\quad \color{red}\bm{\longrightarrow} \quad \color{black} n \rightarrow \boxed{nCr} \rightarrow k \rightarrow \boxed{=}

Pada kalkulator ilmiah CASIO, kunci nCr biasanya memiliki tombol tersendiri atau berada di atas tombol pembagian, tergantung modelnya.

Misalnya kita ingin mengetahui kombinatorial bilangan 10 per 6, kita harus melakukan barisan berikut:

\begin{pmatrix}10\\ 6 \end{pmatrix}\quad \color{red}\bm{\longrightarrow} \quad \color{black} 10 \rightarrow \boxed{nCr} \rightarrow 6 \rightarrow \boxed{=} \rightarrow 210

Penerapan bilangan kombinatorial

Jika Anda sudah sampai sejauh ini, Anda mungkin sudah tahu cara menyelesaikan bilangan kombinatorial apa pun, sempurna. Tapi… bilangan kombinatorial digunakan untuk apa? Nah, selanjutnya kita akan melihat semua keuntungan yang dihadirkan oleh jenis operasi yang sangat istimewa ini.

Kombinatorik

Seperti yang kita lihat di bagian atas halaman, hasil bilangan kombinatorial

\begin{pmatrix}n\\ k \end{pmatrix}

mewakili jumlah kelompok yang mungkin

k

unsur-unsur yang dapat dibentuk dari himpunan yang jumlahnya banyak

n

item.

Oleh karena itu, beberapa masalah kombinatorial dapat diselesaikan dengan menggunakan bilangan kombinatorial (atau koefisien binomial). Mari kita lihat cara melakukannya menggunakan contoh:

  • Dalam suatu kelas yang terdiri dari 30 siswa, kita ingin memilih sekelompok 4 siswa untuk melaksanakan tugas tertentu. Berapa jumlah seluruh kelompok berbeda yang dapat dibentuk?

Dalam hal ini urutan siswa tidak menjadi masalah, siswa yang sama tidak diulang dua kali dalam kelompok, dan tidak semua siswa masuk ke dalam kelompok. Oleh karena itu, rumus bilangan kombinatorial dapat digunakan untuk menentukan banyaknya cara pembentukan suatu kelompok.

Untuk melakukannya, Anda harus menghitung bilangan kombinatorial dengan jumlah siswa sebagai pembilangnya dan dengan banyaknya siswa yang akan membentuk kelompok sebagai urutannya:

\begin{pmatrix}30 \\ 4 \end{pmatrix} =\cfrac{30!}{4!(30-4)!} =\cfrac{30\cdot 29 \cdot 28 \cdot 27 \cdot \cancel{26!}}{4\cdot 3 \cdot 2 \cdot 1 \cdot \cancel{26!}} = \cfrac{657720}{24}=\bm{27405}

Oleh karena itu, jumlah total kombinasi yang mungkin adalah 27.405 kelompok.

binomial Newton

Penerapan bilangan kombinatorial lainnya adalah binomial Newton. Binomial Newton adalah polinomial yang terdiri dari dua suku yang dipangkatkan menjadi bilangan bulat, artinya binomial Newton adalah polinomial yang memenuhi persamaan aljabar berikut:

(a+b)^n

Jelasnya, jika binomial dikuadratkan, ini berarti binomial tersebut merupakan identitas penting dan oleh karena itu, dapat dengan mudah dihitung dengan rumus yang sesuai. Sebaliknya, jika binomial dinaikkan ke angka yang besar, perhitungannya menjadi cukup sulit. Teorema binomial Newton mengatakan bahwa jenis polinomial ini dapat dihitung dengan sangat mudah dari bilangan kombinatorial.

Klik link berikut dan cari tahu apa itu rumus binomial Newton dan cara menghitungnya. Selain itu, Anda akan dapat melihat contoh dan latihan dengan latihan yang diselesaikan langkah demi langkah. Dan akhirnya, Anda akan menemukan sejarah aneh dari teorema ini.

Segitiga Tartaglia (atau Pascal).

Seperti yang telah Anda lihat di seluruh artikel ini, menghitung koefisien binomial bilangan besar secara manual bisa jadi melelahkan dan rumit.

Sebaliknya, dengan segitiga Tartaglia, disebut juga segitiga Pascal, semua bilangan kombinatorial dapat dengan mudah ditentukan menggunakan aturan mnemonik. Ini secara logis sangat berguna karena menghemat banyak waktu selama perhitungan.

Untuk mengetahui secara pasti bagaimana melakukan hal ini, lihat penjelasan segitiga Tartaglia . Di halaman tertaut ini, Anda akan mengetahui apa itu segitiga misterius, kegunaannya (memiliki kegunaan yang mengejutkan) 😮 dan asal usulnya (sudah digunakan lebih dari 1000 tahun yang lalu).

Latihan bilangan kombinatorial terpecahkan

Agar Anda dapat berlatih dan memahami sepenuhnya konsep yang dijelaskan, kami tinggalkan beberapa latihan yang diselesaikan selangkah demi selangkah tentang bilangan kombinatorial.

Latihan 1

Temukan bilangan kombinatorial 9 kali 5 (tanpa menggunakan kalkulator).

Untuk mencari nilai bilangan kombinatorial 9 dari 5 kita cukup menerapkan rumus faktorial:

\begin{pmatrix}9 \\ 5 \end{pmatrix} =\cfrac{9!}{5!(9-5)!} = \cfrac{9\cdot 8 \cdot 7\cdot 6\cdot \cancel{5!}}{\cancel{5!} \cdot (4 \cdot 3 \cdot 2 \cdot 1)}= \cfrac{3024}{24} = \bm{126}

Latihan 2

Berapakah hasil penjumlahan dua bilangan kombinatorial berikut? (tanpa kalkulator)

\begin{pmatrix}10\\ 6 \end{pmatrix} + \begin{pmatrix}10\\ 7 \end{pmatrix}

Dari sifat-sifat bilangan kombinatorial maka jumlah soal sama dengan bilangan kombinatorial berikut:

\begin{pmatrix}10\\ 6 \end{pmatrix} + \begin{pmatrix}10\\ 7 \end{pmatrix}=\begin{pmatrix}11\\ 7 \end{pmatrix}

Oleh karena itu, cukup menghitung bilangan kombinatorial 11 dari 7:

\begin{pmatrix}11 \\ 7 \end{pmatrix} =\cfrac{11!}{7!(11-7)!} = \cfrac{11\cdot 10 \cdot 9\cdot 8 \cdot \cancel{7!}}{\cancel{7!} \cdot (4 \cdot 3 \cdot 2 \cdot 1)}= \cfrac{7920}{24} = \bm{330}

Latihan 3

Tentukan apakah bilangan-bilangan kombinatorial berikut sama:

\begin{pmatrix}6\\ 0 \end{pmatrix} \qquad \begin{pmatrix}6\\ 1 \end{pmatrix}\qquad \begin{pmatrix}6\\ 6 \end{pmatrix}

Untuk mencari hasil ketiga bilangan kombinatorial tidak perlu menggunakan kalkulator, namun dapat dengan mudah ditemukan berkat sifat-sifat bilangan kombinatorial.

Pertama-tama, bilangan kombinatorial dengan bilangan apa pun yang lebih besar dari 0 menghasilkan 1. Oleh karena itu:

\begin{pmatrix}6\\ 0 \end{pmatrix} =1

Sebaliknya, bilangan apa pun yang lebih besar dari satu sama dengan bilangan itu sendiri. Belum:

\begin{pmatrix}6\\ 1 \end{pmatrix} =6

Dan terakhir, bilangan kombinatorial apa pun yang dibentuk oleh bilangan yang sama yang diulang dua kali setara dengan 1. Jadi:

\begin{pmatrix}6\\ 6 \end{pmatrix} =1

Kesimpulannya, bilangan kombinatorial pertama dan ketiga pada soal adalah sama, namun berbeda dengan bilangan kombinatorial tengah.

\begin{pmatrix}6\\ 0 \end{pmatrix}= \begin{pmatrix}6\\ 6 \end{pmatrix}\neq \begin{pmatrix}6\\ 1 \end{pmatrix}

Tinggalkan Komentar

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *

Scroll to Top