Jarak garis ke bidang di ruang angkasa

Di sini Anda akan menemukan cara menghitung jarak dari garis ke bidang dan, sebagai tambahan, Anda akan dapat melihat contoh dan latihan yang diselesaikan langkah demi langkah.

Berapa jarak antara garis dan bidang?

Dalam geometri analitik, jarak antara garis dan bidang dalam ruang bergantung pada posisi relatif antara dua elemen geometri berikut:

Jika garis termasuk dalam bidang atau garis dan bidang sejajar , maka jarak yang memisahkan keduanya adalah nol.
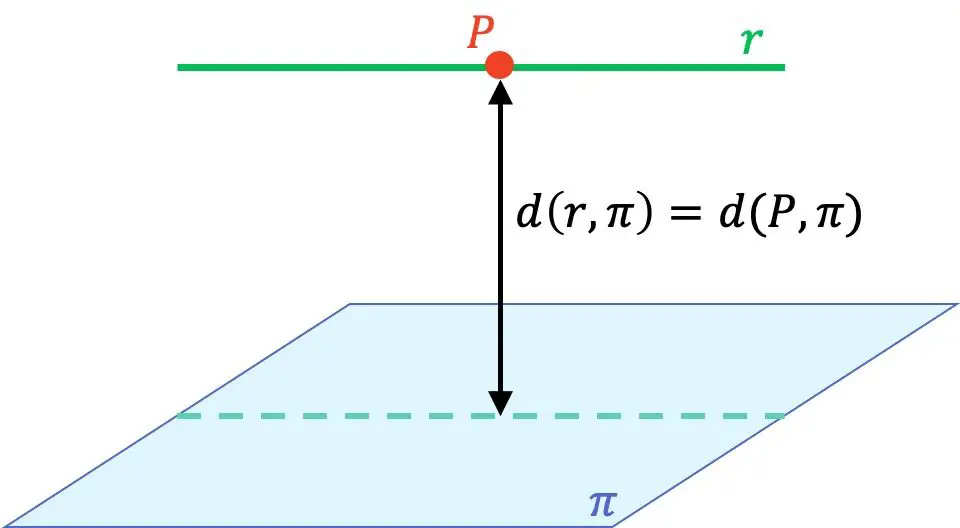
Jika garis sejajar dengan bidang , jarak garis ke bidang ditentukan dengan mengambil titik mana saja pada garis dan menghitung jarak titik tersebut ke bidang.

Oleh karena itu, untuk menghitung jarak garis ke bidang, penting bagi Anda untuk mengetahui cara menentukan posisi relatif antara garis dan bidang dan cara menghitung jarak antara titik dan bidang . Jadi jika Anda belum sepenuhnya paham atau belum mengetahui rumusnya, kami sarankan Anda melihat terlebih dahulu halaman tertaut, di mana Anda akan menemukan penjelasan, contoh, dan latihan yang diselesaikan langkah demi langkah.

Contoh penghitungan jarak antara garis dan bidang

Agar Anda dapat melihat cara mencari jarak antara garis dan bidang di ruang angkasa (di R3), kita akan menyelesaikan soal sebagai contoh:

Seberapa jauh garisnya
$r$

di pesawat

$\pi$

?

$\displaystyle r: \ \begin{cases}x=-2+t \\[1.7ex] y=1-3t \\[1.7ex] z=-1+2t\end{cases}$

$\pi : \ 4x+2y+z-6=0$

Untuk mencari jarak antara garis dan bidang, Anda harus mengetahui terlebih dahulu posisi relatif antara keduanya.

Di satu sisi, garis didefinisikan dalam bentuk persamaan parametrik, sehingga vektor arahnya dan titik yang dilaluinya adalah:

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r =(1,-3,2) \\[2ex] P(-2,1,-1) \end{cases}$

Dan sebaliknya, vektor normal bidang adalah:

$\vv{n} =(4,2,1)$

Jadi, untuk menentukan kedudukan relatif antara bidang dan garis, perlu dihitung hasil kali skalar antara vektor arah garis dan vektor tegak lurus bidang:

$\begin{aligned} \vv{\text{v}}_r \cdot \vv{n} & = (1,-3,2) \cdot (4,2,1) \\[2ex] & = 1 \cdot 4-3 \cdot 2 +2\cdot 1 \\[2ex] &= 4 -6 +2 \\[2ex] & = 0\end{aligned}$

Hasil perkalian titiknya adalah nol, sehingga garis hanya dapat dimuat pada bidang atau sejajar dengannya. Jadi, untuk mengetahui kasusnya, kita substitusikan koordinat kartesius titik pada garis tersebut ke dalam persamaan bidang:

$4x+2y+z-6=0 \ \xrightarrow{P(-2,1,-1)} \ 4\cdot (-2) +2\cdot 1 -1-6= 0$

$-8+2-1-6 = 0$

$-13 \neq 0$

Dengan mensubstitusikan titik garis ke persamaan bidang diperoleh pertidaksamaan, sehingga titik tersebut tidak memperhatikan persamaan bidang dan akibatnya garis dan bidang sejajar.

Setelah kita mengetahui bahwa garis dan bidang sejajar, sekarang kita dapat menghitung jarak geometri antara keduanya. Caranya, kita ambil titik pada garis dan menghitung jarak dari titik tersebut ke bidang.

$P(-2,1,-1) \qquad \qquad \pi: \ 4x+2y+z-6=0$

Jadi, kita menggunakan rumus jarak suatu titik ke bidang:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Sekarang kita substitusikan nilai setiap yang tidak diketahui ke dalam rumus:

$d(P,\pi) = \cfrac{\lvert 4\cdot (-2)+2\cdot 1+1\cdot (-1)-6\rvert}{\sqrt{4^2+2^2+1^2}}$

Dan terakhir, kami melakukan operasi:

$d(P,\pi) = \cfrac{\lvert -8+2-1-6\rvert}{\sqrt{16+4+1}}$

$d(P,\pi) = \cfrac{\lvert -13\rvert}{\sqrt{21}}$

$d(P,\pi) = \cfrac{13}{\sqrt{21}}$

Sehingga jarak garis ke bidang sama dengan jarak titik ke bidang yang dihitung:

$\bm{d(r,\pi)=d(P,\pi) = }\cfrac{\bm{13}}{\bm{\sqrt{21}}}$

Tentunya jarak harus selalu memberi kita nilai positif, karena jarak selalu positif. Jika kita mendapat hasil negatif, berarti kita melakukan kesalahan dalam mengambil langkah.

Berapa jarak antara garis dan bidang?

Contoh penghitungan jarak antara garis dan bidang

Tinggalkan Komentar Batalkan Balasan