▷ Segala sesuatu tentang geometri analitik di ruang angkasa ✅

Di halaman ini Anda akan menemukan penjelasan segala sesuatu tentang geometri analitik dalam ruang (dan rumusnya): persamaan garis dan bidang, posisi relatif antara bidang dan garis, cara menghitung jarak dan sudut dalam ruang,…

Apa itu geometri dalam ruang?

Geometri ruang adalah cabang geometri yang mempelajari bangun-bangun geometri tiga dimensi (3D), yaitu bangun-bangun yang menempati suatu tempat dalam ruang. Seperti kerucut, kubus, limas, bola, silinder, prisma, polihedra, dll.

Namun pada halaman ini kita akan fokus pada geometri analitik dalam ruang , bagian geometri ruang yang fokus pada analisis titik, garis, bidang, jarak antara dua bangun geometri, sudut yang dibentuknya, titik potong antara geometri yang berbeda. angka. elemen, dll.

Persamaan garis dalam ruang

Ingatlah bahwa definisi matematis dari sebuah garis adalah sekumpulan titik-titik berurutan yang diwakili dalam arah yang sama tanpa kurva atau sudut.

Jadi, untuk menyatakan secara matematis setiap garis dalam ruang tiga dimensi (dalam R3) kita menggunakan persamaan garis, dan untuk menemukannya kita hanya memerlukan sebuah titik yang termasuk dalam garis tersebut dan vektor arah garis tersebut.

Hanya dengan dua elemen geometri ini, Anda dapat menemukan semua persamaan garis yang berbeda, yaitu sebagai berikut:

Persamaan garis adalah persamaan vektor , persamaan parametrik , persamaan kontinu , dan persamaan implisit (atau umum) .

Di bawah ini Anda memiliki penjelasan tentang berbagai jenis persamaan garis.

Persamaan vektor garis dalam ruang

$\vv{\text{v}}$

adalah vektor arah garis dan

$P$

suatu titik yang berada di sebelah kanan:

$\vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z) \qquad P(P_x,P_y,P_z)$

Rumus persamaan vektor garis adalah:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y,z)=(P_x,P_y,P_z)+t\cdot (\text{v}_x,\text{v}_y,\text{v}_z) \end{empheq}$

Persamaan parametrik garis dalam ruang

Rumus persamaan parametrik suatu garis dapat diperoleh dari persamaan vektornya dengan menyamakan komponen ke komponen:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases} x=P_x+t\cdot\text{v}_x \\[1.7ex] y=P_y+t\cdot\text{v}_y \\[1.7ex] z=P_z+t\cdot\text{v}_z\end{cases} \end{empheq}$

Persamaan garis kontinu dalam ruang

Rumus persamaan garis kontinu adalah:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cfrac{x-P_x}{\text{v}_x}=\cfrac{y-P_y}{\text{v}_y}= \cfrac{z-P_z}{\text{v}_z} \end{empheq}$

Persamaan garis jenis ini juga dapat diperoleh dari persamaan parametrik, Anda dapat melihat demonstrasi persamaan kontinu di halaman kami, selain itu Anda juga dapat melihat contoh dan latihan dengan latihan persamaan yang diselesaikan di sebelah kanan.

Persamaan umum (atau implisit) garis dalam ruang

Terakhir, dengan mengalikan pecahan persamaan kontinu garis dua dengan dua, kita memperoleh persamaan garis umum (atau implisit) :

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases} A_1x+B_1y+C_1z+D_1=0 \\[1.7ex] A_2x+B_2y+C_2z+D_2=0\end{cases} \end{empheq}$

Persamaan garis seperti ini disebut juga persamaan kartesius.

Kita baru saja melihat 4 persamaan garis yang paling relevan (vektor, parametrik, kontinu, dan umum), namun ada persamaan lain yang agak khusus dan oleh karena itu, diperlukan satu halaman penuh untuk menjelaskannya. Inilah persamaan kanoniknya , di tautan ini Anda dapat melihat penjelasan lengkapnya, mengapa begitu istimewa dan apa yang membedakannya dari yang lain.

Persamaan bidang di luar angkasa

Dalam geometri analitik, persamaan bidang adalah persamaan yang memungkinkan bidang apa pun dinyatakan secara analitis. Jadi, untuk mencari persamaan suatu bidang, Anda hanya memerlukan sebuah titik dan dua vektor bebas linier yang dimiliki oleh bidang tersebut.

Jadi, semua jenis persamaan bidang adalah: persamaan vektor , persamaan parametrik , persamaan implisit (atau umum) , dan persamaan bidang kanonik (atau segmental) .

Selanjutnya kita akan melihat penjelasan dan rumus semua persamaan denahnya.

Persamaan vektor bidang

Diberikan sebuah titik dan dua vektor arah pada suatu bidang:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

Rumus persamaan vektor suatu bidang adalah:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}} \end{empheq}$

Atau setara:

$(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)$

Emas

$\lambda$

Dan

$\mu$

Mereka adalah dua skalar, yaitu dua bilangan real.

Persamaan parametrik bidang

Sedangkan rumus persamaan parametrik bidang adalah:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases} \end{empheq}$

Persamaan bidang implisit atau umum

Persamaan implisit suatu denah, disebut juga persamaan umum, diperoleh dengan menyelesaikan determinan berikut dan menyetel hasilnya ke 0:

$\displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0$

Dengan demikian persamaan implisit atau umum dari rencana yang dihasilkan akan berbentuk sebagai berikut:

Persamaan bidang jenis ini disebut juga persamaan bidang kartesius.

Persamaan bidang kanonik atau segmental

Rumus persamaan kanonik atau segmental suatu bidang adalah sebagai berikut:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cfrac{x}{a}+\cfrac{y}{b} + \cfrac{z}{c} = 1 \end{empheq}$

Emas:

$a$

Ini adalah titik potong antara bidang dan sumbu X.
$b$

Ini adalah titik potong antara bidang dan sumbu Y.
$c$

Di sinilah bidang memotong sumbu Z.

Vektor normal pada bidang

Vektor normal suatu bidang adalah vektor yang tegak lurus terhadap semua garis yang terdapat pada bidang tersebut. Oleh karena itu, vektor yang normal terhadap suatu bidang berarti vektor tersebut tegak lurus terhadap bidang tersebut.

Banyak permasalahan metrik dalam geometri analitik spasial menyangkut bidang dan vektor normalnya. Untuk menyelesaikan latihan ini Anda hanya perlu mengetahui hubungan matematis antara bidang dan vektor normalnya:

Komponen X, Y, Z dari vektor tegak lurus suatu bidang bertepatan dengan koefisien A, B, C dari persamaan implisit (atau umum) bidang tersebut.

$\displaystyle \color{orange} \boxed{ \color{black} \quad \pi : \ Ax+By+C+D = 0 \quad \iff \quad \vv{n} = (A,B,C) \quad \vphantom{\Bigl(}}$

Emas

$\vv{n}$

adalah vektor ortogonal terhadap bidang

$\pi.$

Posisi relatif dua elemen geometris dalam ruang

Jelasnya, sebuah garis atau bidang tidak harus berdiri sendiri dalam ruang, tetapi sebaliknya, mereka biasanya berinteraksi satu sama lain: berpotongan, sejajar, tegak lurus, dll. Nah, pada bagian ini kita akan melihat perbedaan posisi relatif garis dan bidang serta cara penentuannya.

Posisi relatif dua garis dalam ruang

Dalam geometri analitik, ketika bekerja dalam ruang tiga dimensi (dalam R3) ada 4 kemungkinan posisi relatif antara dua garis: dua garis dapat berupa garis berimpit , garis sejajar , garis potong , atau garis potong .

Garis sejajar

Dua garis dikatakan sejajar jika arah keduanya sama tetapi tidak mempunyai titik yang sama. Selain itu, garis sejajar selalu memiliki jarak yang sama satu sama lain.

Garis yang bertepatan

posisi relatif dari dua garis yang berhimpitan

Dua garis berhimpitan jika arahnya sama dan semua titiknya bersekutu.

Garis persimpangan

kedudukan relatif dua garis yang berpotongan

Dua garis berpotongan mempunyai arah yang berbeda namun bersentuhan pada satu titik.

Garis persimpangan

Dua garis yang berpotongan mempunyai arah yang berbeda dan tidak berpotongan di titik manapun. Oleh karena itu, dua garis yang bersilangan tidak berada pada bidang yang sama. Misalnya pada representasi grafis di atas garis

$s$

selalu di depan garis lurus

$r$

, jadi mereka tidak akan pernah saling bersentuhan.

Cara mencari posisi relatif dua garis berdasarkan rentang

Salah satu cara mencari posisi relatif dua baris adalah dengan menghitung rentang dua matriks tertentu, seperti yang akan kita lihat di bawah. Cara ini sangat berguna bila kedua garis dinyatakan dalam bentuk persamaan implisit (atau umum).

Jadi, jika kita mempunyai dua garis yang dinyatakan dengan persamaan implisit (atau umum) dalam ruang tiga dimensi (dalam R3):

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}A_3x+B_3y+C_3z+D_3=0 \\[2ex] A_4x+B_4y+C_4z+D_4=0 \end{cases}$

Misalkan A adalah matriks yang terdiri dari koefisien dua garis:

$\displaystyle A=\begin{pmatrix}A_1 & B_1 & C_1\\[1.1ex]A_2 & B_2 & C_2\\[1.1ex]A_3 & B_3 & C_3\\[1.1ex]A_4 & B_4 & C_4 \end{pmatrix}$

Dan diketahui matriks A’ yang diperluas, yaitu matriks yang terbentuk dari semua parameter kedua garis:

$\displaystyle A'=\begin{pmatrix}A_1 & B_1 & C_1&D_1\\[1.1ex]A_2 & B_2 & C_2&D_2\\[1.1ex]A_3 & B_3 & C_3&D_3\\[1.1ex]A_4 & B_4 & C_4&D_4 \end{pmatrix}$

Kemudian kedudukan relatif kedua garis tersebut dapat ditentukan berdasarkan luasan kedua matriks sebelumnya sesuai tabel berikut:

posisi relatif dua garis berdasarkan rentang

Oleh karena itu, untuk mencari posisi relatif antara dua baris kita harus menghitung rentang kedua matriks dan bergantung pada rentang masing-masing matriks, hal ini akan tergantung pada satu atau lain kasus.

Teorema ini dapat dibuktikan dengan menggunakan teorema Rouché-Frobenius (metode yang digunakan untuk menyelesaikan sistem persamaan linear), namun pada halaman ini kami tidak akan melakukan pembuktiannya karena cukup rumit dan tidak menambah banyak. .

Posisi relatif dua bidang dalam ruang

Dalam geometri analitik, hanya ada tiga kemungkinan posisi relatif antara dua bidang: bidang berpotongan, bidang sejajar, dan bidang berimpit.

Bidang berpotongan : dua bidang berpotongan jika hanya berpotongan pada satu garis.
Bidang sejajar : Dua bidang sejajar jika tidak berpotongan di titik mana pun.
Bidang-bidang yang bersinggungan : dua bidang dikatakan berhimpitan jika kedua bidang tersebut mempunyai titik-titik yang sama.

Tembakan berpotongan

posisi relatif dua bidang yang berpotongan

bidang paralel

Rencana yang cocok

kedudukan relatif dua bidang yang berhimpitan

Cara menentukan posisi relatif dua bidang berdasarkan koefisien

Salah satu cara untuk mengetahui posisi relatif antara dua bidang adalah dengan menggunakan koefisien persamaan umum (atau implisit).

Pertimbangkan persamaan umum (atau implisit) dari dua bidang berbeda:

$\pi_1 : \ Ax+By+Cz+D=0$

$\pi_2 : \ A'x+B'y+C'z+D'=0$

Posisi relatif antara dua bidang dalam ruang tiga dimensi bergantung pada proporsionalitas koefisien atau parameternya:

posisi relatif dua bidang dengan parameter

Jadi, kedua bidang akan berpotongan jika salah satu koefisien A, B, atau C tidak sebanding dengan koefisien lainnya. Sebaliknya, kedua bidang akan sejajar jika hanya suku-suku independennya saja yang tidak proporsional. Dan terakhir, rencana tersebut akan bertepatan jika semua koefisien dari kedua persamaan tersebut sebanding.

Jarak dalam ruang

Di bawah ini Anda mempunyai rumus untuk menghitung jarak antara berbagai elemen geometri: antara titik dan garis, antara dua bidang, antara bidang dan garis,…

Jarak antara dua titik

Jarak antara dua titik sesuai dengan norma vektor yang ditentukan oleh 2 titik tersebut.

Jadi jika kita memiliki dua poin umum:

$A(a_x,a_y,a_z) \qquad \qquad B(b_x,b_y,b_z)$

Rumus jarak kedua titik tersebut adalah:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(A,B) = \vert \vv{AB} \rvert = \sqrt{(b_x-a_x)^2+(b_y-a_y)^2+(b_z-a_z)^2} \end{empheq}$

Jarak suatu titik ke suatu garis

Rumus untuk menghitung jarak suatu titik ke garis dalam ruang adalah:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert} \end{empheq}$

Emas:

$\lvert \vv{\text{v}}_r \rvert$

adalah modul vektor arah garis

$r.$
$Q$

adalah titik di sebelah kanan

$r,$

$P$

suatu titik pada garis tersebut

$s$

Dan

$\vv{QP}$

vektor yang ditentukan oleh dua titik
$\lvert \vv{QP} \times \vv{\text{v}}_r \rvert$

adalah modulus perkalian vektor antar vektor

$\vv{QP}$

Dan

$\vv{\text{v}}_r$

Jarak antara dua garis

Jarak antara dua garis bergantung pada posisi relatifnya:

Jika kedua garis tersebut berimpit atau berpotongan , maka jarak kedua garis tersebut sama dengan nol, karena keduanya berpotongan (setidaknya) di satu titik.
Jika kedua garis sejajar atau berpotongan, rumus harus diterapkan tergantung kasusnya (kedua penjelasan tersedia di bawah).

Jarak antara dua garis sejajar

Dua garis sejajar selalu berjarak sama. Jadi untuk menghitung jarak antara dua garis sejajar di ruang (di R3) caranya sama seperti di bidang (di R2): Anda hanya perlu mengambil satu titik di salah satu dari dua garis tersebut dan mencari jaraknya. adalah dari titik ini ke jalur lainnya.

Jadi untuk menentukan jarak antara 2 garis sejajar harus menggunakan rumus jarak antara titik dan garis.

Jarak antara dua garis yang berpotongan

Misalkan vektor arah dan titik mana pun pada dua garis yang berpotongan adalah:

$\displaystyle r: \ \begin{cases} \vv{\text{u}} \\[2ex] A\end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}} \\[2ex] B\end{cases}$

Rumus jarak antara dua garis yang berpotongan adalah:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert} \end{empheq}$

Emas:

$\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|$

adalah nilai mutlak hasil kali campuran vektor-vektor tersebut

$\vv{\text{u}}, \vv{\text{v}}$

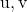
dan vektor yang ditentukan oleh titik-titik

$A$

Dan

$B$

.
$\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert$

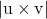
adalah modulus hasil kali vektor antara vektor arah dua garis bersilangan.

Meskipun Anda mempunyai rumusnya di sini, menentukan jarak antara dua garis yang berpotongan ternyata lebih rumit dari yang terlihat. Jadi jika anda ingin berlatih di link berikut anda dapat melihat contoh dan latihan soal jarak antara dua garis yang berpotongan.

Jarak dari suatu titik ke bidang

Diberikan sebuah titik dan persamaan umum (atau implisit) sebuah bidang:

$P(x_0,y_0,z_0) \qquad \qquad \pi: \ Ax+By+Cz+D=0$

Rumus jarak suatu titik ke bidang adalah:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}} \end{empheq}$

Jika dengan menerapkan rumus tersebut diperoleh hasil yang sama dengan nol, berarti jarak antara titik dan bidang adalah nol, sehingga titik tersebut merupakan bagian dari bidang tersebut.

Jarak antara dua pesawat

Jarak antara dua bidang di ruang angkasa bergantung pada posisi relatif antara kedua bidang tersebut:

Jika kedua bidang tersebut berpotongan atau berhimpitan maka jarak keduanya sama dengan nol karena berpotongan pada suatu titik tertentu.
Jika kedua bidang sejajar , maka jarak kedua bidang dihitung dengan mengambil sebuah titik pada salah satu bidang tersebut dan menghitung jarak antara titik tersebut dengan bidang lainnya.

Jarak antara dua bidang sejajar

Dua bidang sejajar selalu mempunyai jarak yang sama satu sama lain, sehingga untuk mencari jarak antara dua bidang sejajar kita dapat mengambil sebuah titik pada salah satu dari dua bidang tersebut dan menghitung jarak dari titik tersebut ke bidang lainnya.

Jadi untuk menghitung jarak antara dua bidang sejajar anda harus mencari titik pada salah satu dari kedua bidang tersebut kemudian menggunakan rumus jarak antara titik dan bidang.

Sudut dalam ruang

Seperti halnya jarak, penentuan sudut antara dua benda geometris dalam ruang bergantung pada karakteristik geometrinya. Karena menghitung sudut yang dibentuk oleh dua garis tidak sama dengan menghitung sudut yang dibentuk oleh dua bidang. Jadi di bawah ini Anda memiliki rumus mencari sudut antara garis dan bidang.

Sudut antara dua garis

Untuk mengetahui sudut antara dua garis dalam ruang Euclidean, kita harus menghitung sudut yang dibentuk oleh vektor arahnya, oleh karena itu:

Diketahui vektor arah dari dua garis yang berbeda:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y,\text{u}_z)\qquad \vv{\text{v}} = (\text{v}_x,\text{v}_y,\text{v}_z)$

Sudut yang dibentuk kedua garis tersebut dapat dihitung dengan rumus berikut:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cos(\alpha) =\cfrac{\lvert \vv{\text{u}} \cdot \vv{\text{v}}\rvert}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert} \end{empheq}$

Emas

$\lvert \vv{\text{u}} \rvert$

Dan

$\lvert \vv{\text{v}} \rvert$

adalah modul dari vektor

$\vv{\text{u}}$

Dan

$\vv{\text{v}}$

masing-masing.

Ingatlah bahwa rumus modulus suatu vektor adalah:

$\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{ \text{v}_x^2+\text{v}_y^2+\text{v}_z^2}$

Sudut antara dua bidang

Sudut antara dua bidang sama dengan sudut yang dibentuk oleh vektor-vektor normal bidang tersebut. Oleh karena itu, untuk mencari sudut antara dua bidang, kita menghitung sudut yang dibentuk oleh vektor-vektor normalnya, karena keduanya ekuivalen .

Mengingat persamaan umum (atau implisit) dari dua bidang berbeda:

$\pi_1 : \ A_1x+B_1y+C_1z+D_1=0$

$\pi_2 : \ A_2x+B_2y+C_2z+D_2=0$

Vektor normal setiap bidang adalah:

$\vv{n}_1=(A_1,B_1,C_1)$

$\vv{n}_2=(A_2,B_2,C_2)$

Dan sudut yang dibentuk oleh kedua bidang tersebut ditentukan dengan menghitung sudut yang dibentuk oleh vektor-vektor normalnya dengan menggunakan rumus sebagai berikut:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cos(\alpha) =\cfrac{\lvert \vv{n}_1 \cdot \vv{n}_2\rvert}{\lvert \vv{n}_1 \rvert \cdot \lvert \vv{n}_2 \rvert} \end{empheq}$

Sudut antara garis dan bidang

Sudut yang dibentuk oleh garis dan bidang didefinisikan sebagai sudut terkecil di antara dua sudut yang saling melengkapi yang dibentuk oleh vektor arah garis dan vektor normal bidang.

Oleh karena itu, jika

$\vv{\text{v}}$

adalah vektor arah garis dan

$\vv{n}$

adalah vektor normal terhadap bidang:

$\vv{\text{v}} = (\text{v}_x,\text{v}_y,\text{v}_z)$

$\vv{n}=(n_x,n_y,n_z)$

Rumus yang digunakan untuk menghitung sudut yang dibentuk oleh garis dan bidang adalah:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \text{sen}(\alpha)=\cfrac{\lvert \vv{\text{v}} \cdot \vv{n}\rvert}{\lvert \vv{\text{v}} \rvert \cdot \lvert \vv{n} \rvert} \end{empheq}$

Geometri analitik dalam ruang (rumus)

Apa itu geometri dalam ruang?

Persamaan garis dalam ruang

Persamaan vektor garis dalam ruang

Persamaan parametrik garis dalam ruang

Persamaan garis kontinu dalam ruang

Persamaan umum (atau implisit) garis dalam ruang

Persamaan bidang di luar angkasa

Persamaan vektor bidang

Persamaan parametrik bidang

Persamaan bidang implisit atau umum

Persamaan bidang kanonik atau segmental

Vektor normal pada bidang

Posisi relatif dua elemen geometris dalam ruang

Posisi relatif dua garis dalam ruang

Cara mencari posisi relatif dua garis berdasarkan rentang

Posisi relatif dua bidang dalam ruang

Cara menentukan posisi relatif dua bidang berdasarkan koefisien

Jarak dalam ruang

Jarak antara dua titik

Jarak suatu titik ke suatu garis

Jarak antara dua garis

Jarak antara dua garis sejajar

Jarak antara dua garis yang berpotongan

Jarak dari suatu titik ke bidang

Jarak antara dua pesawat

Jarak antara dua bidang sejajar

Sudut dalam ruang

Sudut antara dua garis

Sudut antara dua bidang

Sudut antara garis dan bidang

Tinggalkan Komentar Batalkan Balasan