▷ Aturan rantai (turunan): latihan yang diselesaikan

Di sini Anda akan mempelajari apa itu aturan rantai dan cara menurunkan fungsi menggunakan aturan rantai. Selain itu, Anda akan dapat melihat beberapa contoh turunan yang diselesaikan dengan aturan rantai dan Anda bahkan dapat berlatih dengan latihan penyelesaian langkah demi langkah pada turunan yang menerapkan aturan rantai.

Apa aturan rantainya?

Aturan rantai adalah rumus yang digunakan untuk menurunkan fungsi komposit. Aturan rantai menyatakan bahwa turunan suatu fungsi komposit f(g(x)) sama dengan turunan f'(g(x)) dikalikan dengan turunan g'(x) .

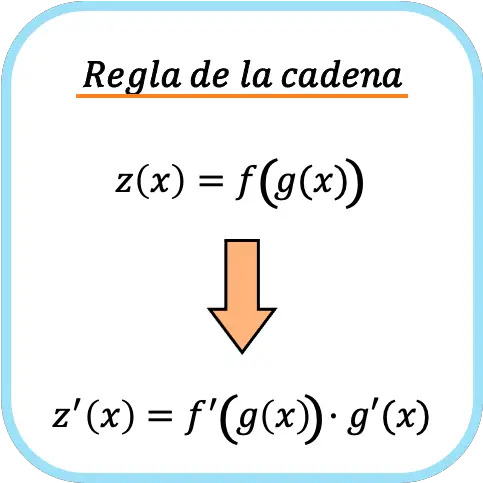
➤ Lihat: fungsi komposit

Secara informal, aturan rantai sering dikatakan untuk mendiferensiasikan suatu fungsi kemudian mengalikannya dengan apa yang ada di dalamnya .

Rumus aturan rantai memungkinkan kita untuk membedakan fungsi majemuk dengan lebih mudah, karena jika kita ingin membedakan komposisi fungsi menggunakan limit definisi turunannya, kita harus melakukan banyak perhitungan.

Di sisi lain, harus diingat bahwa aturan ini hanya digunakan untuk mencari turunan dari fungsi majemuk, dan bukan untuk jenis fungsi atau operasi apa pun dengan fungsi. Misalnya, kesalahan yang sangat umum adalah melakukan kesalahan dan menerapkan aturan rantai pada produk fungsional seperti berikut:

$\ln(x)\cdot x^2$

❌

Aturan rantai hanya dapat digunakan jika kita memiliki satu fungsi di dalam fungsi lainnya .

$\ln(x^2)$

✅

Contoh turunan dengan aturan rantai

Dengan mengetahui definisi aturan rantai, kita akan memperoleh beberapa fungsi dengan aturan rantai sebagai contoh. Ingatlah bahwa jika dalam contoh Anda tidak memahami bagaimana suatu fungsi diturunkan dengan aturan rantai, Anda dapat bertanya kepada kami di komentar!

Contoh 1

Dalam contoh ini, kita akan menggunakan aturan rantai untuk menurunkan logaritma natural dari x kuadrat:

$f(x)=\ln(x^2)$

Turunan logaritma natural sama dengan 1 kali argumennya, jadi turunannya

$f'\bigl(g(x)\bigr)$

menjadi:

$f(x)=\ln(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{u}$

$f\bigl(g(x)\bigr)=\ln(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'\bigl(g(x)\bigr)=\cfrac{1}{x^2}$

Sebaliknya, turunan x yang dipangkatkan dua adalah 2x:

$g(x)=x^2\quad\color{orange}\bm{\longrightarrow}\quad\color{black} g'(x)=2x$

Terakhir, kita menghitung turunan seluruh fungsi dengan menerapkan aturan rantai. Turunan dari fungsi komposit tersebut adalah hasil kali dua turunan yang baru kita temukan:

$z(x)=f\bigl(g(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=\ln(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{x^2}\cdot 2x = \cfrac{2x}{x^2}=\cfrac{2}{x}$

Contoh 2

Dalam contoh kedua ini, kita akan menurunkan fungsi potensial berdasarkan polinomial:

$f(x)=\left(3x^2+4x-5\right)^3$

Untuk memperoleh suatu pangkat, kita perlu menempatkan eksponen asli di depannya dan mengurangkan satu satuan dari eksponen tersebut, sehingga turunan fungsi potensial tanpa menerapkan aturan rantai adalah:

$f\bigl(g(x)\bigr)=\left(3x^2+4x-5\right)^3 \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'\bigl(g(x)\bigr)=3\left(3x^2+4x-5\right)^2$

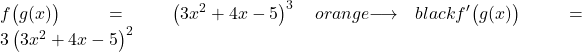
Sekarang kita simpulkan apa yang ada di dalam tanda kurung:

$g(x)=3x^2+4x-5\quad\color{orange}\bm{\longrightarrow}\quad\color{black} g'(x)=6x+4$

Dan terakhir, kita menggunakan aturan rantai untuk menyelesaikan turunan seluruh fungsi, yang merupakan perkalian dua turunan yang dihitung sebelumnya:

$z(x)=f\bigl(g(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=\left(3x^2+4x-5\right)^3 \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=3\left(3x^2+4x-5\right)^2\cdot (6x+4)$

Contoh 3

Dalam hal ini, kita akan mencari turunan sinus dari x pangkat tiga ditambah 7x:

$f(x)=\text{sen}(x^3+7x)$

Memang benar, ini adalah komposisi fungsi karena kita mempunyai fungsi x ³ +7x di dalam fungsi sinus, oleh karena itu kita dapat menggunakan aturan rantai untuk mencari turunan dari fungsi komposit tersebut.

Di satu sisi, turunan sinus adalah kosinus, sehingga turunan fungsi luarnya adalah kosinus dengan argumen yang sama dengan sinus:

$f\bigl(g(x)\bigr)=\text{sen}(x^3+7x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'\bigl(g(x)\bigr)=\text{cos}(x^3+7x)$

Sebaliknya turunan dari x ³ +7x adalah 3x ² +7.

$g(x)=x^3+7x\quad\color{orange}\bm{\longrightarrow}\quad\color{black} g'(x)=3x^2+7$

Oleh karena itu, turunan fungsi komposit adalah hasil kali kedua turunannya:

$z(x)=f\bigl(g(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=\text{sen}(x^3+7x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cos}(x^3+7x)\cdot (3x^2+7)$

Menyelesaikan latihan turunan dengan aturan rantai

Latihan 1

Turunkan fungsi komposit berikut menggunakan aturan rantai:

$f(x)=\left(5x^2-6x\right)^3$

Lihat solusinya

Fungsi eksterior merupakan fungsi potensial, sehingga untuk menghitung turunannya harus menggunakan rumus berikut:

$f\bigl(g(x)\bigr)=a\bigl(g(x)\bigr)^n \ \longrightarrow \ f'\bigl(g(x)\bigr)=n\cdot a\bigl(g(x)\bigr)^{n-1}$

$f\bigl(g(x)\bigr)=\left(5x^2-6x\right)^3\ \longrightarrow \ f'\bigl(g(x)\bigr)= 3\left(5x^2-6x\right)^2$

Dan kemudian kita menghitung turunan dari fungsi di dalamnya. Ini adalah pengurangan pangkat, jadi untuk menghitung turunannya Anda harus menerapkan rumus berikut untuk setiap sukunya:

$f(x)=ax^n \ \longrightarrow \ f'(x)=n\cdot ax^{n-1}$

$g(x)=5x^2-6x\ \longrightarrow$

$g'(x)=2\cdot 5x^1-1 \cdot 6 x^0 =10x-6$

Singkatnya, turunan fungsi komposit adalah hasil kali dua turunan yang ditemukan:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=\left(5x^2-6x\right)^3 \ \longrightarrow \ \bm{f'(x)= 3\left(5x^2-6x\right)^2\cdot (10x-6)}$

Latihan 2

Selesaikan turunan fungsi komposit berikut menggunakan aturan rantai:

$f(x)=-3\left(5x^5+9x^3\right)^4$

Lihat solusinya

Pertama, kita cari turunan fungsi eksteriornya:

$\begin{aligned} f\bigl(g(x)\bigr) \ \longrightarrow \ f'\bigl(g(x)\bigr) & =4 \cdot ( -3) \left(5x^5+9x^3\right)^3 \\[1.5ex]&=-12\left(5x^5+9x^3\right)^3 \end{aligned}$

Dan sekarang kita selesaikan turunan dari fungsi interior:

$g(x)=5x^5+9x^3\ \longrightarrow \ g'(x)=25x^4+27x^2$

Oleh karena itu, turunan dari seluruh fungsi adalah:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=-3\left(5x^5+9x^3\right)^4 \ \longrightarrow \ \bm{f'(x)=-12\left(5x^5+9x^3\right)^3\cdot \left(25x^4+27x^2\right)}$

Latihan 3

Hitung turunan komposisi fungsi berikut dengan aturan rantai:

$f(x)=e^{2x^3}$

Lihat solusinya

Ini adalah fungsi eksponensial, jadi untuk menghitung turunannya Anda harus menerapkan rumus berikut:

$f(x)=e^{x} \ \longrightarrow \ f'(x)=e^{x}$

$f\bigl(g(x)\bigr)=e^{2x^3} \ \longrightarrow \ f'\bigl(g(x)\bigr)= e^{2x^3}$

Kami juga membedakan fungsi dari eksponen fungsi:

$g(x)=2x^3 \ \longrightarrow \ g'(x)=6x^2$

Dan kami menggunakan aturan rantai untuk mencari turunan dari fungsi komposit bilangan bulat:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=e^{2x^3} \ \longrightarrow \ \bm{f'(x)= e^{2x^3}\cdot 6x^2}$

Latihan 4

Temukan turunan dari fungsi komposit berikut menggunakan aturan rantai:

$f(x)=\sqrt[3]{\text{sen}(x) +x }$

Lihat solusinya

Ini adalah komposisi fungsi, karena kita memiliki fungsi sinusoidal dan fungsi linier dalam argumen fungsi irasional. Jadi kita hitung dulu turunan dari akarnya:

$f(x)=\sqrt[n]{x} \ \longrightarrow \ f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

$f\bigl(g(x)\bigr)=\sqrt[3]{\text{sen}(x) +x } \ \longrightarrow \ f'\bigl(g(x)\bigr)= \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }}$

Dan sekarang kita mengambil argumen dari kaum radikal. Ini adalah penjumlahan fungsi, jadi turunannya adalah jumlah turunan tiap suku:

$g(x)=\text{sen}(x) +x \ \longrightarrow \ g'(x)=\cos(x) + 1$

Jadi, turunan seluruh fungsi sama dengan perkalian dua turunan yang dihitung:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\begin{aligned}f(x)=\sqrt[3]{\text{sen}(x)+x} \ \longrightarrow \ f'(x)& = \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }} \cdot \bigl(\cos(x) + 1 \bigr)\\[1.5ex]&=\cfrac{\bm{\cos(x) + 1}}{\bm{3\sqrt[3]{\bigl(\mathbf{sen}(x) +x\bigr)^2} }}\end{aligned}$

Latihan 5

Turunkan komposisi fungsi berikut menggunakan aturan rantai:

$f(x)=3^{x^2+5}$

Lihat solusinya

Untuk menerapkan aturan rantai, Anda harus mencari turunan pangkat dan polinomial, lalu mengalikannya. Jadi, kita memperoleh pangkat menggunakan rumus yang sesuai:

$f(x)=a^x \ \longrightarrow \ f'(x)=a^x\cdot \ln (a)$

$f\bigl(g(x)\bigr)=3^{x^2+5} \ \longrightarrow \ f'\bigl(g(x)\bigr)= 3^{x^2+5}\cdot \ln(3)$

Kedua, kita memperoleh fungsi polinomial dari eksponen:

$g(x)=x^2+5 \ \longrightarrow \ g'(x)=2x$

Dan aturan rantai memberitahu kita bahwa turunan seluruh fungsi adalah hasil kali turunan yang baru kita temukan:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=3^{x^2+5} \ \longrightarrow \ \bm{f'(x)= 3^{x^2+5}\cdot \ln(3) \cdot 2x}$

Latihan 6

$f(x)=\ln \bigl(4x^2 \cdot \cos(x) \bigr)$

Lihat solusinya

Jelasnya, fungsi dalam soal ini adalah fungsi komposit, karena dalam argumen logaritma natural kita memiliki produk dari dua jenis fungsi yang berbeda. Jadi kita bedakan dulu logaritmanya:

$f(x)=\ln(x) \ \longrightarrow \ f'(x)=\cfrac{1}{x}$

$f\bigl(g(x)\bigr)=\ln \bigl(4x^2 \cdot \cos(x) \bigr) \ \longrightarrow \ f'\bigl(g(x)\bigr)= \cfrac{1}{4x^2 \cdot \cos(x) }$

Kedua, kita memperoleh fungsi dari argumen logaritma. Ini adalah perkalian dua fungsi, jadi Anda harus menggunakan rumus berikut untuk melakukan turunannya:

$z(x)=f(x) \cdot g(x) \ \longrightarrow \ z'(x)=f'(x)\cdot g(x)+f(x) \cdot g'(x)$

$\begin{aligned}g(x)=4x^2 \cdot \cos(x) \ \longrightarrow \ g'(x) & = 8x\cdot \cos(x) + 4x^2 \cdot \bigl(- \text{sen}(x)\bigr) \\[2ex] & = 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x)\end{aligned}$

Jadi, turunan seluruh fungsi, menurut aturan rantai, akan menjadi hasil kali kedua turunannya:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\begin{aligned}f'(x)&= \cfrac{1}{4x^2 \cdot \cos(x) } \cdot \bigl( 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x) \bigr)\\[1.5ex]&=\cfrac{8x\cdot \cos(x) - 4x^2 \cdot\text{sen}(x)}{4x^2 \cdot \cos(x)}\\[1.5ex]&=\cfrac{\bm{2\cos(x) - x \cdot }\mathbf{sen}\bm{(x)}}{\bm{x \cdot \cos(x) }}\end{aligned}$

Latihan 7

Selesaikan turunan fungsi berikut dengan menggunakan aturan rantai:

$f(x)=\log_9 (e^{x^2}-6x^7)$

Lihat solusinya

Ini adalah komposisi fungsi, jadi kita akan membedakan logaritma dan argumennya secara terpisah lalu mengalikan turunannya.

Jadi, pertama-tama kita bedakan logaritmanya ke basis 9:

$f(x)=\log_a (x) \ \longrightarrow \ f'(x)=\cfrac{1}{x\cdot \ln (a)}$

$f\bigl(g(x)\bigr)=\log_9 (e^{x^2}-6x^7) \ \longrightarrow \ f'\bigl(g(x)\bigr)=\cfrac{1}{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)}$

Dan sekarang kita menghitung turunan dari argumen logaritma. Perhatikan bahwa bilangan e mempunyai fungsi dalam argumennya, yaitu fungsi komposit, jadi kita juga perlu menerapkan aturan rantai untuk menurunkan fungsi ini:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$h(x)=e^{x^2} \ \longrightarrow \ h'(x)=e^{x^2}\cdot \bigl(x^2\bigr)' =e^{x^2}\cdot 2x$

Jadi, turunan dari argumen bilangan bulat logaritma adalah:

$g(x)= e^{x^2}-6x^7\ \longrightarrow \ g'(x)=e^{x^2}\cdot 2x - 42x^6$

Dan terakhir, turunan seluruh fungsi adalah hasil kali f'(g(x)) dan g'(x):

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\begin{aligned}f'(x)&=\cfrac{1}{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)} \cdot \bigl(e^{x^2}\cdot 2x - 42x^6\bigr)\\[1.5ex]&=\cfrac{\bm{e^{x^2}\cdot 2x - 42x^6}}{\bm{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)}}\end{aligned}$

Latihan 8

Turunkan fungsi komposit berikut menggunakan aturan rantai:

$f(x)=\text{sen}\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr)$

Lihat solusinya

Dalam latihan ini kita mempunyai komposisi beberapa fungsi, jadi kita harus menerapkan aturan rantai beberapa kali. Pertama-tama kita turunkan fungsi trigonometri dari sinus, yang turunannya adalah kosinus:

$f\bigl(g(x)\bigr)=\text{sen}\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr)\ \longrightarrow \ f'\bigl(g(x)\bigr)=\cos\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr)$

Dan sekarang kita menghitung turunan dari argumen sinus menggunakan aturan rantai:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\begin{aligned} g(x)= \Bigl( 9x^5 + \cos(x) \Bigr)^2 \cdot g'(x) &= 2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(9x^5 + \cos(x) \Bigr)' \\[1.5ex]&=2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(45x^4-\text{sen}(x)\Bigr)\end{aligned}$

Terakhir, kita memperoleh turunan seluruh komposisi fungsi dengan menerapkan kembali aturan rantai:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\bm{f'(x)=\cos } \bm{\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr) \cdot 2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(45x^4-}\mathbf{sen}\bm{(x)\Bigr)}$

Bukti Aturan Rantai

Terakhir, kita akan membuktikan rumus aturan rantai. Untuk melakukan ini, kita akan mulai dari definisi matematis dari turunan:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Misalkan z adalah fungsi yang terdiri dari dua fungsi:

$z=f\bigl(g(x)\bigr)$

Maka turunan dari fungsi z yang menerapkan definisi tersebut adalah:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{h}$

Seperti yang sudah Anda ketahui, Anda bisa mengalikan dan membagi pecahan dengan suku yang sama, karena hal ini tidak mengubah hasilnya. Oleh karena itu, kita dapat melanjutkan ke langkah berikutnya:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{h}\cdot \frac{g(x+h)-g(x)}{g(x+h)-g(x)}$

Kami mengatur ulang penyebut pecahan:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{g(x+h)-g(x)}\cdot \frac{g(x+h)-g(x)}{h}$

Dengan menerapkan sifat-sifat limit, kita dapat membagi limit di atas menjadi dua. Karena limit suatu hasil kali sama dengan hasil kali limitnya:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{g(x+h)-g(x)}\cdot \lim_{h \to 0}\frac{g(x+h)-g(x)}{h}$

Dan ungkapan ini setara dengan berikut ini:

$\displaystyle z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

Oleh karena itu, rumus aturan rantai terbukti karena kita mendapatkannya dari definisi turunan.

Apa aturan rantainya?

Contoh turunan dengan aturan rantai

Contoh 1

Contoh 2

Contoh 3

Menyelesaikan latihan turunan dengan aturan rantai

Latihan 1

Latihan 2

Latihan 3

Latihan 4

Latihan 5

Latihan 6

Latihan 7

Latihan 8

Bukti Aturan Rantai

Tinggalkan Komentar Batalkan Balasan