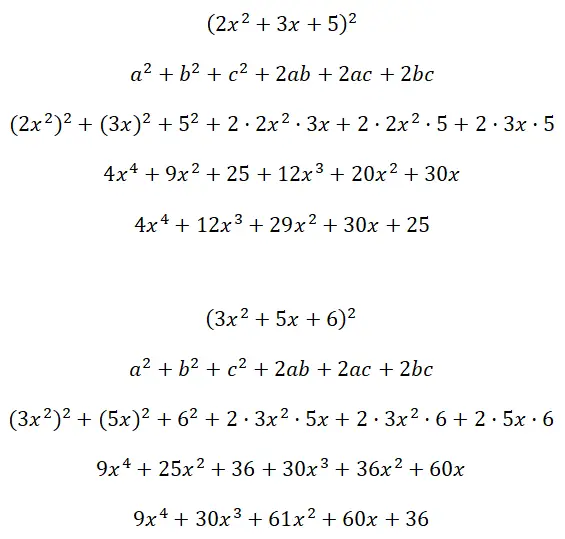Produk atau identitas luar biasa apa yang dimaksud?
Identitas luar biasa , juga disebut produk luar biasa atau persamaan luar biasa , adalah sumber daya matematika yang memungkinkan produk dan hasil bagi polinomial diselesaikan dengan lebih cepat. Seperti yang ditunjukkan oleh kata identitas, ini adalah persamaan yang memungkinkan kita menghitung operasi ini tanpa harus menyelesaikannya. Karena kita tahu bahwa ungkapan ini mengikuti aturan tetap (yang selalu dipenuhi) dan oleh karena itu, kita bisa mendapatkan hasilnya tanpa harus memeriksanya.
Kapan menggunakan identitas penting?
Identitas ini terutama digunakan dalam bidang aljabar dan fungsi utamanya adalah untuk mempercepat penyelesaian polinomial tertentu, tanpa harus menyelesaikan seluruh operasi itu sendiri. Dari sana kami memperoleh formula produk terkenal yang akan kami komentari sepanjang artikel. Dan terakhir, kita dapat menerapkan rumus tersebut untuk menyelesaikan kuadrat, polinomial faktor , atau jenis penghitungan lainnya.
Bagaimana cara mengatasi produk yang luar biasa selangkah demi selangkah?
Untuk menyelesaikan identitas penting, Anda perlu mengikuti prosedur yang sangat sederhana, yang juga sangat masuk akal:
- Identifikasi jenis identitas penting: Langkah pertama adalah mengidentifikasi jenis operasi: produk penting atau hasil bagi penting. Anda juga harus memperjelas jenis rumus apa yang perlu Anda terapkan, meskipun Anda akan memahaminya nanti, setelah kami menjelaskan berbagai jenis identitas penting.
- Terapkan rumusnya: Setelah Anda mengetahui rumus mana yang perlu Anda terapkan, sekarang saatnya melakukan perhitungan. Bergantung pada jenis identitasnya, Anda harus menyelesaikan operasi yang lebih atau kurang rumit dan dalam sebagian besar kasus, perhitungan ini akan terdiri dari suku-suku yang mengandung setidaknya satu hal yang tidak diketahui.
- Sederhanakan ekspresi: Terakhir, ketika Anda mendapatkan hasilnya, Anda perlu menyederhanakannya. Pada langkah ini, Anda perlu mengelompokkan suku-suku serupa dan mengurutkannya untuk membentuk hasil polinomial yang terstruktur dengan baik. Perlu dicatat bahwa langkah ini sama pentingnya dengan langkah lainnya, karena jika tidak, latihan ini akan tetap tidak lengkap.
Rumus identitas terkenal atau produk utama yang terkenal
Di bawah ini Anda akan menemukan semua rumus yang berhubungan dengan identitas terkenal. Selain penjelasan teoritis dari setiap kasus, ada juga beberapa contoh produk penyelesaian yang penting, yang melaluinya Anda akan memahami semua konsep dengan lebih baik. Perlu disebutkan bahwa di bagian pertama ini Anda hanya akan menemukan identitas yang paling penting . Namun, dengan membaca artikel ini, Anda akan mempelajari cara mengembangkan produk terkenal yang lebih kompleks, seperti produk trinomial.
kuadrat dari suatu jumlah
Kasus pertama berkaitan dengan kuadrat jumlah , yang merupakan ekspresi polinomial yang sangat umum di dunia aljabar. Ini dapat ditemukan ditulis sebagai: (a + b) 2 , yang setara dengan: (a + b) · (a + b). Oleh karena itu, kita tahu bahwa penyelesaiannya dapat dilakukan dengan perkalian polinomial. Namun berkat identitas terkenal, kita dapat menghemat waktu dengan menggunakan rumus berikut: (a + b) 2 = a 2 + 2ab + b 2 . Selanjutnya kami tunjukkan demonstrasi rumus yang baru saja kami lihat, dengan cara ini Anda akan dapat memahami dari mana asalnya dan bagaimana penggunaannya:
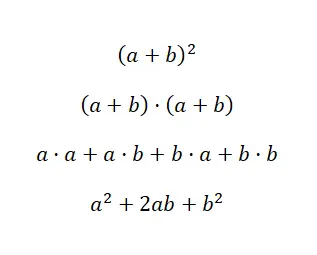
Seperti yang bisa kita lihat, kita melakukan verifikasi dengan menggunakan perkalian polinomial yang telah kita komentari sebelumnya. Dan kami dapat mengatakan dengan pasti bahwa jika Anda hafal rumus yang dihasilkan, maka dengan melakukan substitusi nilai yang sederhana, Anda bisa mendapatkan hasilnya lebih cepat. Jadi ini adalah konsep matematika yang sangat berguna. Sekarang setelah Anda mengetahui cara kerja kuadrat suatu jumlah, kami akan menunjukkan contoh nyata:
Contoh kuadrat suatu jumlah
Hitung identitas penting (2x + 4) 2 :
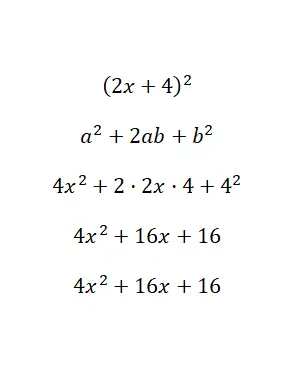
Pada dasarnya, kami mengaitkan nilai binomial dengan huruf-huruf rumus dan menyelesaikannya: a = 2x dan b = 4. Akhirnya, setelah menyelesaikan semua perhitungan, kami memperoleh polinomial 4x 2 + 16x + 16, yaitu setara dengan aslinya . Dalam contoh ini, kita memperoleh polinomial diperluas (dalam bentuk standar) dari polinomial tereduksi.
kuadrat pengurangan
Ekspresi umum lainnya adalah kuadrat pengurangan , yang sangat mirip dengan kuadrat penjumlahan, hanya berubah satu tanda. Maka struktur binomialnya ekuivalen dengan: (a – b) 2 , dan jika kita buka, kita peroleh: (a – b) · (a – b). Seperti pada kasus sebelumnya, hal ini dapat dihitung dari perkalian polinomial, meskipun juga memiliki rumus yang memudahkan penyelesaiannya: a 2 – 2ab +b 2 . Di bawah ini Anda dapat menemukan bukti empirisnya:
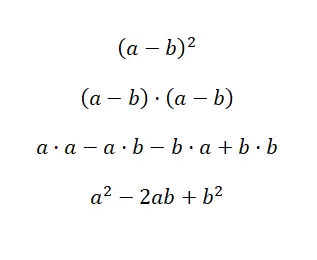
Untuk menyederhanakan penyelesaian kuadrat suatu selisih, kita dapat menggunakan rumus yang sama dengan yang kita gunakan untuk jumlah kuadrat, tetapi dengan tanda pertama negatif . Perubahan minimal ini memungkinkan ekspresi disesuaikan dengan binomial yang terdiri dari suku positif dan suku negatif, yang berguna untuk pengurangan. Kami sekarang akan menunjukkan kepada Anda contoh penyelesaiannya:
Contoh kuadrat pengurangan
Hitung identitas penting (x – 3) 2 :
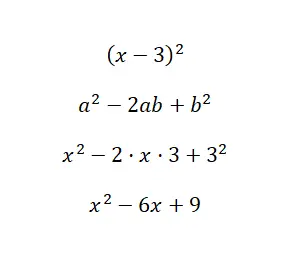
Seperti yang bisa kamu lihat pada contoh penyelesaiannya, kita mensubstitusikan nilai binomial kita ke dalam rumus a = x dan b = 3. Oleh karena itu, dengan menggunakan rumus yang telah kita jelaskan sebelumnya, kita hanya tinggal melakukan substitusi dan beberapa hal yang sangat mendasar. perhitungan. Hal ini memungkinkan kita melihat betapa mudahnya menghitung kuadrat selisih dengan ekspresi ini.
Selisih kuadrat atau jumlah karena selisih
Kasus ketiga dari perkalian penting disebut selisih kuadrat , yang dibentuk oleh perkalian binomial positif dan binomial negatif. Ekspresi gaya ini memiliki struktur sebagai berikut: (a + b) · (a – b), jadi jika kita memperluas hasil kali ini kita memperoleh rumus yang memudahkan perhitungan: a 2 – b 2 . Seperti yang Anda lihat, ini adalah rumus yang sangat sederhana, meskipun untuk memahaminya sepenuhnya Anda perlu mengembangkan semua perhitungan:
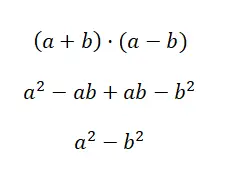
Contoh penjumlahan berdasarkan selisih
Hitung identitas penting (x + 1) · (x – 4):
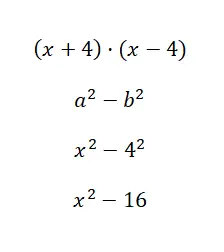
Pada kesempatan kali ini perhitungan numeriknya sangat mudah, sebenarnya kita hanya perlu menyelesaikan suatu pangkat. Meskipun benar rumus ini hanya berlaku jika binomial memiliki suku pokok yang sama dan suku bebas yang sama, tetapi dengan tanda yang berubah. Jadi identitas ini penting, tapi ini bukan identitas yang paling sering Anda gunakan.
Hasil kali dua binomial dengan suku yang sama
Dalam kasus keempat ini, kita menghadapi situasi yang sangat mirip dengan situasi sebelumnya, meskipun dengan sedikit modifikasi pada strukturnya. Perhatikan perbedaan yang kami tunjukkan: (x + a) · (x + b) dan (a + b) · (a – b). Jika Anda masih belum melihatnya dengan jelas, perhatikan contoh berikut: (x + 4) · (x + 5) dan (x + 4) · (x – 4). Dalam kasus pertama ( hasil perkalian dua binomial suku yang sama ) hanya ada satu suku yang sama, sedangkan dalam kasus kedua (jumlah selisihnya) kedua suku tersebut adalah persekutuan, tetapi suku bebas memiliki tanda terbalik. Karena itu, mari kita lihat rumus apa yang bisa kita gunakan:
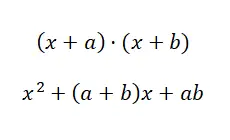
Contoh hasil kali dua binomial dengan suku yang sama
Selesaikan hasil kali penting (x + 2) · (x + 3):
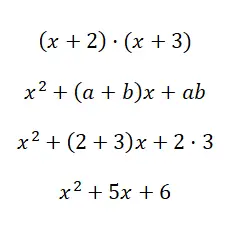
Dengan menggunakan rumus x 2 + (a + b)x + ab kita dapat menghitung polinomial derajat kedua hasil perkalian kedua binomial tersebut. Kami berharap melalui contoh ini Anda telah memahami perbedaan antara dua kasus terakhir yang kami jelaskan, karena terkadang sulit untuk membedakannya.
kuadrat dari trinomial
Saat kami mencoba menghitung kuadrat trinomial, kami juga mendapatkan produk luar biasa yang membuat hidup kami lebih mudah. Ekspresi ini direpresentasikan seperti ini: (a + b + c) 2 dan hasil kali ekuivalennya adalah: a 2 + b 2 + c 2 + 2ab + 2ac + 2bc. Perlu dicatat bahwa ini berlaku untuk trinomial positif, tetapi jika salah satu koefisiennya negatif, Anda hanya perlu menuliskan nilai negatifnya ke dalam rumus. Di bawah ini adalah demonstrasi rumusnya:
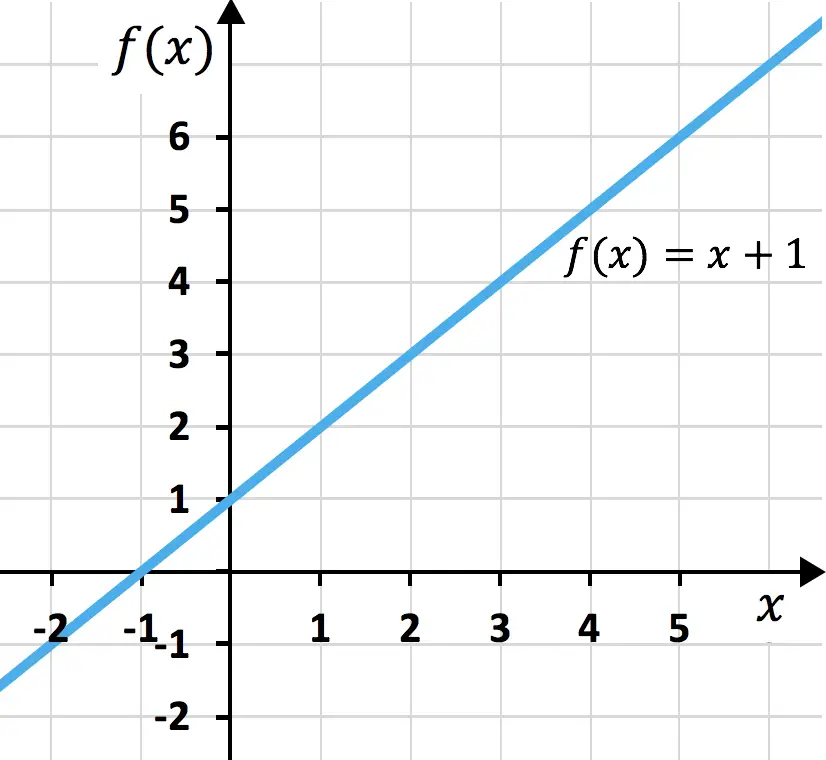
Contoh kuadrat trinomial
Hitung identitas penting (2x + 1 + x 2 ) 2 :
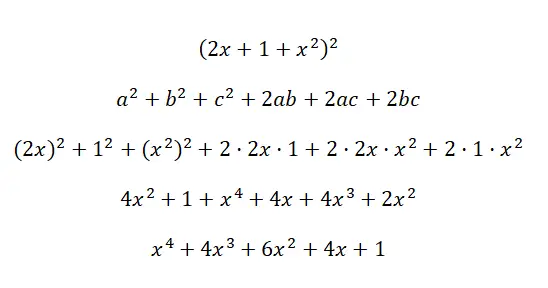
Formula identitas yang luar biasa atau produk kubus yang luar biasa
Sekarang setelah kita menjelaskan identitas penting utama, kita akan melihat turunannya , dimulai dengan binomial pangkat tiga. Untuk menghitung produk terkenal dengan gaya ini, kita harus menggunakan rumus yang sedikit lebih rumit, namun mengikuti struktur yang mirip dengan rumus yang telah kita bahas.
binomial potong dadu
Kubus suatu binomial ditulis: (a + b) 3 dan (a – b) 3 , persamaan ini setara dengan rumus berikut: (a 3 + 3a 2 b + 3ab 2 + b 3 ), dan (a 3 – 3a 2 b + 3ab 2 – b 3 ). Kedua kasus ini disebut pangkat tiga jumlah dan pangkat tiga pengurangan, karena keduanya merupakan binomial pangkat tiga. Di bawah ini Anda akan menemukan demonstrasi yang sangat rinci dari setiap kasus:
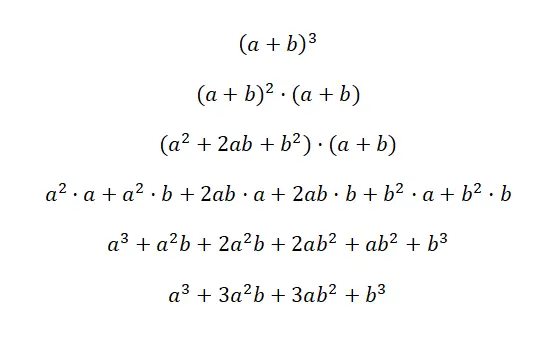
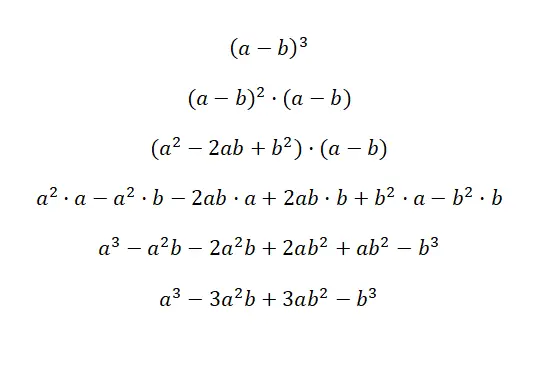
Kunci untuk memahami pembuktian pertama ini adalah dengan memahami bahwa (a + b) 3 ekuivalen dengan: (a + b) 2 · (a + b). Dengan cara ini, kita menggunakan rumus kuadrat suatu jumlah yang telah kita jelaskan sebelumnya untuk mengalikan faktor lainnya. Kemudian kita cukup menyederhanakan ekspresi tersebut, dan kita memperoleh identitas penting yang sesuai: a 3 + 3a 2 b + 3ab 2 + b 3 . Dalam kasus contoh kedua, hal yang sama terjadi, tetapi dengan perubahan tanda.
Contoh kubus binomial
Selesaikan identitas penting (x + 3) 3 :
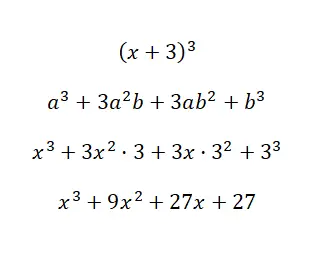
Dengan menggunakan rumus yang baru saja kita bahas, kita dapat menghitung polinomialnya, dengan memperhatikan bahwa: a = xyb = 3. Seperti yang Anda lihat, prosedurnya sangat sederhana dan tidak banyak kerumitan dalam perhitungannya, itu karena kita memiliki rumusnya . Jika tidak, melakukan perkalian sebanyak itu akan sangat membosankan.
Jumlah kubus dan selisih kubus
Kita juga mempunyai kasus lain yang mudah tertukar dengan kasus sebelumnya. Meskipun kedua kasus tersebut ditulis berbeda, namun keduanya tidak setara. Ekspresi yang setara dengan jumlah atau selisih kubus adalah: a 3 + b 3 , sedangkan pada kasus sebelumnya kita berbicara tentang: (a + b) 3 . Seperti yang Anda lihat, ada kesamaan yang tidak dapat disangkal dalam struktur ekspresi, tetapi kenyataannya, ketika mengembangkan perhitungan, keduanya adalah kasus yang sangat berbeda:
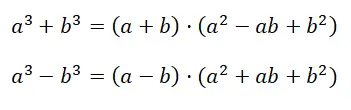
Dalam demonstrasi rumus kita memperoleh faktorisasi polinomial pertama , tepatnya kita beralih dari binomial awal ke hasil kali binomial dengan trinomial. Tampaknya hasil yang diperoleh (a + b) · (a 2 – ab + b 2 ), tidak menyederhanakan perhitungan sama sekali, namun kenyataannya, dengan memfaktorkan polinomial tersebut kita memperoleh ekspresi yang sangat mudah dipahami.
Contoh penjumlahan kubus
Hitung produk penting x 3 + 27:
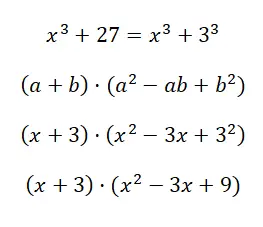
Dalam hal ini hasil yang kita peroleh cukup panjang, karena tidak bisa disederhanakan lagi. Namun, ekspresi ini adalah hal yang normal, pada kenyataannya, dalam kasus ini Anda hanya dapat memperoleh hasil dengan struktur yang setara dengan produk binomial dan trinomial, seperti dalam contoh ini.
trinomial potong dadu
Kubus suatu trinomial ditulis: (a + b + c) 3 , yang berarti mengalikan tiga trinomial identik, tetapi tanpa eksponen: (a + b + c) · (a + b + c) · (a + b + c). Ini adalah perkalian paling rumit yang pernah ada, meskipun rumusnya cukup logis dan diperoleh dengan cara yang sama seperti semua perkalian polinomial yang sesuai. Di bawah ini Anda akan menemukan bukti rumus identitas luar biasa ini:
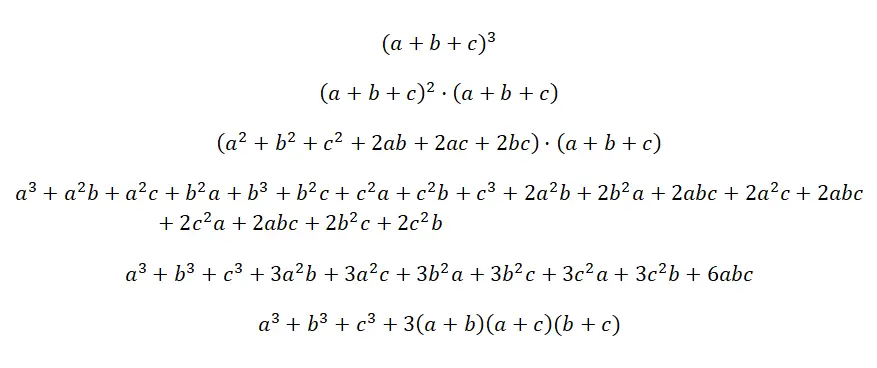
Contoh kubus trinomial
Selesaikan kubus trinomial berikut (x 2 + 3x – 4) 3 :
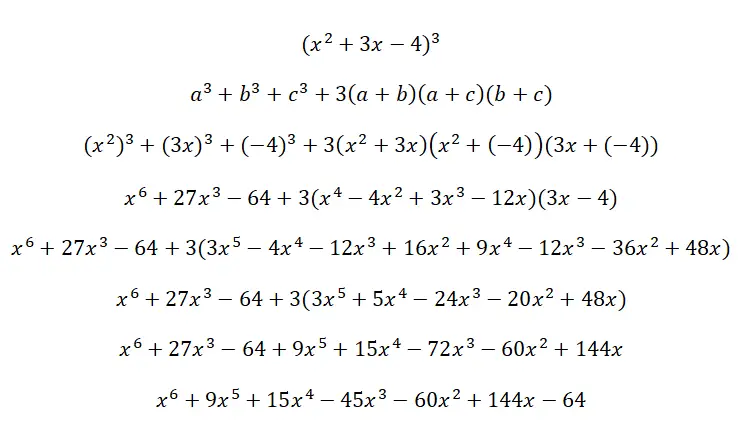
rasio yang luar biasa
Terakhir, kami akan menjelaskan hasil bagi penting , yang merupakan identitas penting untuk menyelesaikan jenis pecahan aljabar tertentu dengan cepat. Lebih tepatnya, ada empat tipe berbeda, yang memiliki satu karakteristik yang sama: hasilnya terdiri dari polinomial eksak (dengan sisa sama dengan nol). Perlu juga disebutkan bahwa rumus hasil bagi luar biasa mempunyai hubungan tertentu dengan rumus hasil kali luar biasa yang telah kami jelaskan.
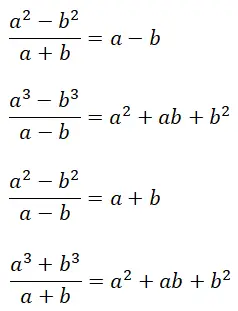
Contoh Rasio Luar Biasa yang Terselesaikan
Hitung rasio penting berikut:
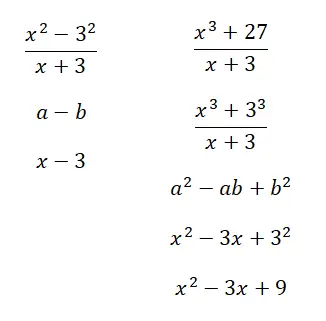
Latihan Produk Luar Biasa Terpecahkan
Sekarang setelah Anda mengetahui cara penyelesaian berbagai masalah penting, inilah waktunya bagi Anda untuk berlatih sedikit. Inilah sebabnya kami menawarkan Anda 6 latihan untuk menerapkan semua teori yang dijelaskan. Dan kami tunjukkan kepada Anda tabel identitas penting utama, sehingga Anda memilikinya saat Anda menyelesaikan semua latihan:

Latihan 1
Selesaikan kuadrat binomial (x – 4) 2 , (x + 1) 2 dan (x – 3) 2 :
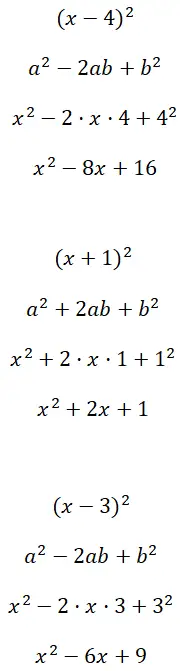
Latihan 2
Hitunglah dua selisih kuadrat (x – 1) · (x + 1) dan (x + 3) · (x – 3):
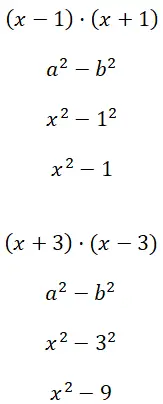
Latihan 3
Kembangkan hasil kali penting pada kubus (x – 5) 3 dan (x + 8) 3 :
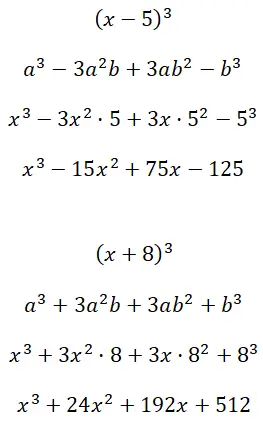
Latihan 4
Kembangkan identitas penting yang dibentuk dari suku multifaktor (4x 2 + 5y) 2 , (5x 3 + y 2 ) · (5x 3 – y 2 ) dan (5xy 2 – 2xy) 2 :
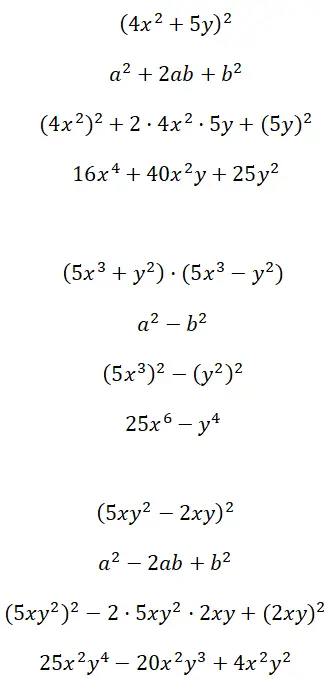
Latihan 5
Hitung hasil kali kubik penting yang dibentuk oleh suku multifaktor (3x 2 + y) 3 dan (5y 3 – 2x 2 ) 3 :
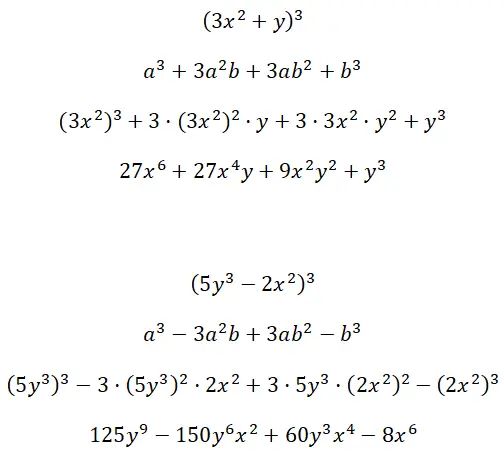
Latihan 6
Selesaikan kuadrat trinomial (2x 2 + 3x + 5) 2 dan (3x 2 + 5x + 6):