Posisi relatif dua garis dalam ruang

Di sini Anda akan menemukan semua posisi relatif dua garis dalam ruang (di R3). Selain itu, dijelaskan cara mencari posisi relatif antara dua garis menggunakan 2 metode yang mungkin: berdasarkan rentang atau dari suatu titik dan vektor setiap garis. Anda bahkan akan dapat melihat contoh dan latihan yang diselesaikan langkah demi langkah.

Berapakah kedudukan relatif dua garis dalam ruang?

Dalam geometri analitik, ketika bekerja dalam ruang tiga dimensi (dalam R3) ada 4 kemungkinan posisi relatif antara dua garis: dua garis dapat berupa garis penggabungan , garis sejajar , garis potong , atau garis potong .

Garis sejajar

Dua garis dikatakan sejajar jika arahnya sama tetapi tidak mempunyai titik persekutuan. Selain itu, garis sejajar selalu memiliki jarak yang sama satu sama lain.

garis yang bertepatan

posisi relatif dari dua garis yang berhimpitan

Dua garis berhimpitan jika arahnya sama dan terlebih lagi jika semua titiknya bersekutu.

garis-garis yang berpotongan

kedudukan relatif dua garis yang berpotongan

Dua garis berpotongan mempunyai arah yang berbeda namun bersentuhan pada satu titik.

Garis persimpangan

Dua garis yang berpotongan mempunyai arah yang berbeda dan tidak berpotongan di titik manapun. Oleh karena itu, dua garis yang bersilangan tidak berada pada bidang yang sama. Misalnya pada representasi grafis di atas garis

$s$

selalu terdepan

$r$

, jadi mereka tidak akan pernah saling bersentuhan.

Ada 2 cara untuk mengetahui posisi relatif antara dua garis, karena keduanya bergantung pada cara persamaan kedua garis dinyatakan:

Jika garis-garisnya berbentuk vektor, parametrik, atau persamaan kontinu, yang terbaik adalah menghitung posisi relatif dari suatu titik dan vektor setiap garis (penjelasan metode ini diberikan di bawah).
Sebaliknya, jika suatu garis didefinisikan dalam bentuk persamaan implisit (atau umum), maka akan lebih mudah untuk mengetahui posisi relatif antara dua garis tersebut dengan menghitung pangkat dua matriks (lihat penjelasan di bawah).

Menentukan kedudukan relatif dua garis dari suatu titik dan suatu vektor

Anda dapat mengetahui posisi relatif antara dua garis dengan titik dan vektor pada setiap garis. Metode ini cocok digunakan ketika garis didefinisikan dalam bentuk persamaan vektor, persamaan parametrik, atau persamaan kontinu.

Jadi, misalkan vektor arah dan titik mana pun pada kedua garis tersebut adalah:

$\displaystyle r: \ \begin{cases} \vv{\text{v}} = (\text{v}}_x, \text{v}}_y,\text{v}}_z})\\[2ex] P(P_x,P_y,P_z)\end{cases} \qquad\qquad s: \ \begin{cases} \vv{\text{v}}' = (\text{v}}_x', \text{v}}_y',\text{v}}_z'})\\[2ex] P'(P_x',P_y',P_z')\end{cases}$

Jadi, untuk mencari posisi relatif dua garis, kita perlu mengikuti prosedur berikut:

‣ Hal pertama yang perlu kita lakukan adalah melihat apakah vektor kedua garis sebanding atau tidak dan, bergantung pada kasusnya, kita melakukan hal berikut:

Jika kedua vektornya sebanding, maka garis-garisnya bisa sejajar atau berimpit. Oleh karena itu kita harus memeriksa apakah titik pada satu garis memenuhi persamaan garis lainnya:
- Jika titik suatu garis memenuhi persamaan garis yang lain, berarti kedua garis tersebut berimpit.
- Jika tidak, berarti kedua garis tersebut sejajar.
Jika kedua vektor tidak sebanding, maka garis tersebut dapat berpotongan atau berpotongan. Dalam hal ini kita harus menyelesaikan determinan 3×3 berikut:

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$
- Jika determinan sebelumnya sama dengan nol, maka kedua garis tersebut berpotongan di suatu titik (berpotongan).
- Jika determinan sebelumnya berbeda dengan nol, maka kedua garis tersebut berpotongan.

Grafik berikut merangkum seluruh prosedur:

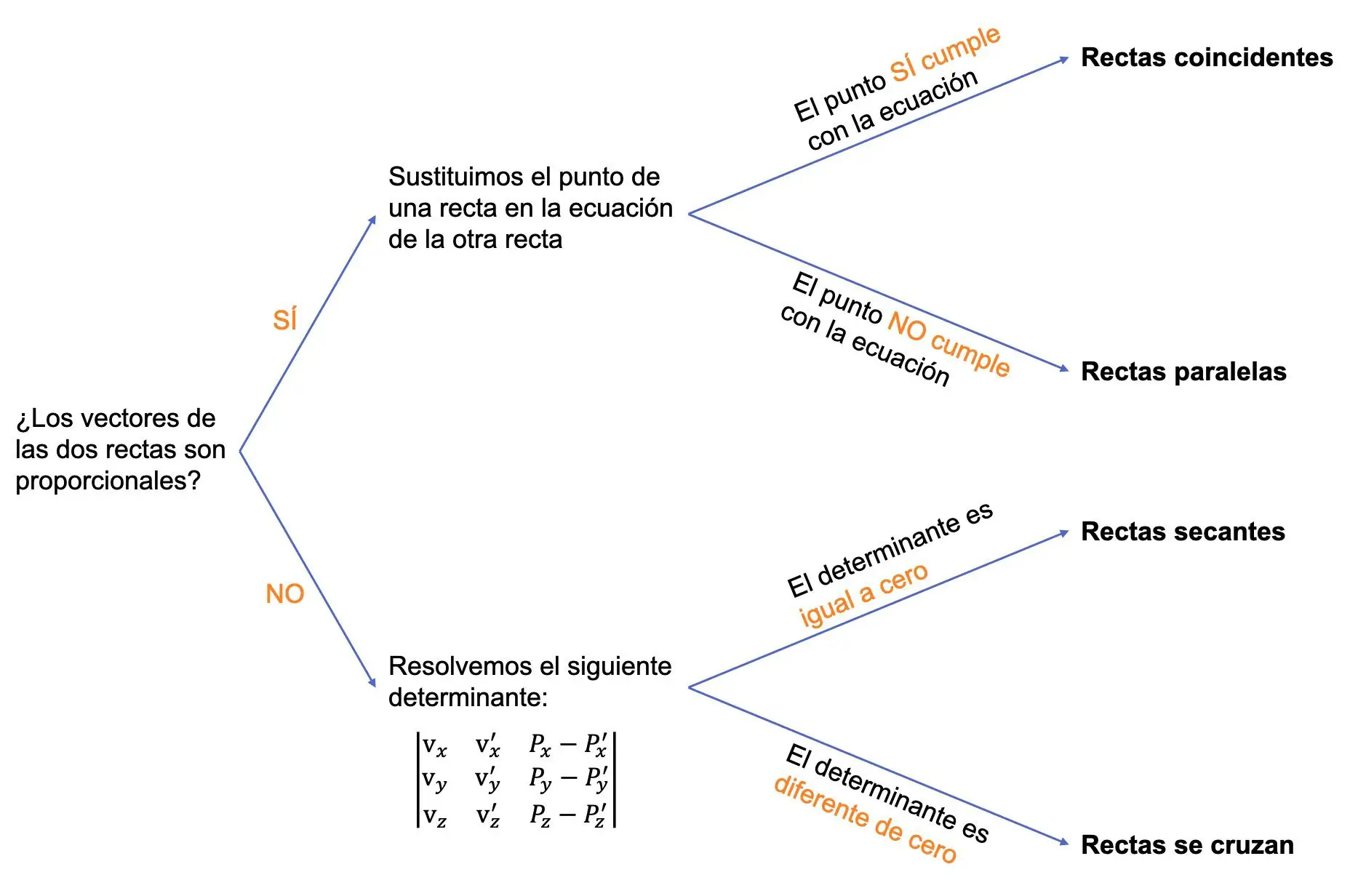
Contoh penentuan posisi relatif antara dua garis

Prosedur sebelumnya mungkin tampak sedikit rumit, namun agar Anda dapat melihat bahwa justru sebaliknya, kami akan menyelesaikan masalah sebagai contoh:

Tentukan posisi relatif antara dua garis berikut:

$r: \ (x,y,z)=(2,0,1)+t(4,-1,1)$

$s: \ (x,y,z)=(1,-3,1)+t(1,2,0)$

Kedua garis tersebut dinyatakan sebagai persamaan vektor, dengan vektor arah setiap garis adalah:

$\vv{r} =(4,-1,1) \qquad \qquad \vv{s}=(1,2,0)$

Dan titik yang dilalui setiap garis adalah:

$R(2,0,1)\qquad \qquad S(1,-3,1)$

Setelah kita mengetahui suatu titik dan vektor arah setiap garis, kita menerapkan metode yang terlihat di atas. Pertama-tama, kita harus memeriksa apakah koordinat vektor-vektornya proporsional:

$\cfrac{4}{1} \neq \cfrac{-1}{2} \neq \cfrac{1}{0} \quad \longrightarrow \quad \text{No proporcionales}$

Karena kedua vektor tersebut tidak sebanding satu sama lain, maka garis-garis tersebut hanya dapat bersinggungan atau bersilangan. Oleh karena itu, sekarang kita perlu menyelesaikan determinan berikut yang dibentuk oleh vektor arah dan sebuah titik pada setiap garis:

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$

Kami mengganti nilainya ke dalam rumus:

$\begin{vmatrix} 4 & 1 & 2-1 \\[1.1ex] -1 & 2 & 0-(-3) \\[1.1ex]1& 0 & 1-1 \end{vmatrix}$

Dan kami menghitung determinannya, untuk ini Anda dapat menggunakan metode apa pun (aturan Sarrus, metode komplemen atau kofaktor, dll.):

$\begin{vmatrix} 4 & 1 & 1 \\[1.1ex] -1 & 2 & 3 \\[1.1ex]1& 0 & 0 \end{vmatrix} = 1$

Jika hasil penentuannya nol, berarti garis tersebut bersilangan (bersentuhan). Namun determinannya berbeda dengan 0 sehingga garisnya berpotongan .

Temukan posisi relatif dua baris demi baris

Cara lain untuk mencari posisi relatif dua baris adalah dengan menghitung pangkat dua matriks beton, seperti yang akan kita lihat selanjutnya. Cara ini sangat berguna bila kedua garis berada dalam bentuk persamaan implisit (atau umum).

Jadi, jika kita mempunyai dua garis yang dinyatakan dengan persamaan implisit (atau umum) dalam ruang tiga dimensi (dalam R3):

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}A_3x+B_3y+C_3z+D_3=0 \\[2ex] A_4x+B_4y+C_4z+D_4=0 \end{cases}$

Misalkan A adalah matriks yang terdiri dari koefisien dua garis:

$\displaystyle A=\begin{pmatrix}A_1 & B_1 & C_1\\[1.1ex]A_2 & B_2 & C_2\\[1.1ex]A_3 & B_3 & C_3\\[1.1ex]A_4 & B_4 & C_4 \end{pmatrix}$

Dan diketahui matriks A’ yang diperluas, yaitu matriks yang dibentuk oleh semua parameter kedua garis:

$\displaystyle A'=\begin{pmatrix}A_1 & B_1 & C_1&D_1\\[1.1ex]A_2 & B_2 & C_2&D_2\\[1.1ex]A_3 & B_3 & C_3&D_3\\[1.1ex]A_4 & B_4 & C_4&D_4 \end{pmatrix}$

Kemudian posisi relatif kedua baris tersebut dapat ditentukan oleh range kedua matriks sebelumnya sesuai tabel berikut:

Oleh karena itu, untuk mencari posisi relatif antara dua baris kita harus menghitung rangking kedua matriks dan bergantung pada rangking masing-masing matriks, hal tersebut akan tergantung pada satu atau lain kasus.

Teorema ini dapat dibuktikan dengan menggunakan teorema Rouché-Frobenius (metode yang digunakan untuk menyelesaikan sistem persamaan linear), namun pada halaman ini kami tidak akan melakukan pembuktiannya karena cukup rumit dan tidak menambah banyak.

Contoh cara mencari posisi relatif dua garis berdasarkan rentang

Setelah kita melihat teori tentang posisi relatif antara dua garis demi baris, mari kita lihat bagaimana teori tersebut dipraktikkan melalui sebuah contoh:

Temukan posisi relatif dari dua garis berikut:

$\displaystyle r: \ \begin{cases}3x+2y+z+4=0 \\[2ex] 4x+2z+2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}3x+4z-1=0 \\[2ex] x-5y-2z-2=0 \end{cases}$

Kedua garis tersebut berbentuk persamaan umum (atau implisit), sehingga kita akan menggunakan metode rangking untuk mencari posisi relatif antara kedua garis tersebut. Oleh karena itu, kita membuat matriks A dan matriks perluasan A’ dengan koefisien garis:

$\displaystyle A=\begin{pmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{pmatrix}$

Setelah kita memiliki kedua matriks, kita perlu menghitung rank masing-masing matriks. Pertama kita hitung rank matriks A berdasarkan determinannya:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4 \end{vmatrix} = -20 \bm{\neq 0}$

$rg(A)=3$

Matriks A memuat determinan submatriks 3×3 bukan nol, sehingga matriks A mempunyai rangking 3 .

Dan sekarang kita menghitung ruang lingkup matriks A’ yang diperluas. Matriks A’ setidak-tidaknya akan selalu berada pada rangking matriks A, yang dalam hal ini bernilai 3, jadi cukup diperiksa apakah matriks tersebut berpangkat 4 atau berpangkat 3. Untuk melakukannya, kita selesaikan determinannya dari matriks 4× 4 dengan penjumlahan (atau kofaktor):

$rg(A')= \ ?$

$\displaystyle det(A')=\begin{vmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{vmatrix} =$

$\displaystyle =3 \cdot\begin{vmatrix} 0 & 2&2\\[1.1ex] 0 & 4&-1\\[1.1ex] -5 & -2 &-2 \end{vmatrix}-2\cdot\begin{vmatrix}4 & 2&2\\[1.1ex]3 & 4&-1\\[1.1ex]1 & -2 &-2 \end{vmatrix}+1\cdot\begin{vmatrix}4 & 0 &2\\[1.1ex]3 & 0 & -1\\[1.1ex]1 & -5 & -2 \end{vmatrix}-4\cdot \begin{vmatrix}4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{vmatrix}$

$\displaystyle =3 \cdot 50-2\cdot(-50)+1\cdot(-50)-4\cdot 50$

$\displaystyle =150+100-50-200$

$\displaystyle \bm{=0}$

$rg(A')=3$

Penentu seluruh matriks yang diperluas adalah nol, sehingga matriks A’ juga berpangkat 3 .

Jadi matriks A dan matriks A’ mempunyai rangking 3 sehingga kedua garis tersebut berpotongan . Artinya, hanya ada satu titik potong di antara keduanya.

$\color{orange} \boxed{\color{black} \quad rg(A) = rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Secantes} \quad \vphantom{\Bigl(}}$

Ingatlah bahwa di atas terdapat tabel yang merangkum semua kemungkinan kasus posisi relatif antara dua garis menurut rentang matriks A dan A’.

Menyelesaikan masalah kedudukan relatif antara dua garis dalam ruang

Latihan 1

Temukan posisi relatif antara dua garis berikut:

$r: \ (x,y,z)=(3,4,0)+t(2,1,-3)$

$s: \ (x,y,z)=(1,-2,2)+t(0,5,1)$

lihat solusi

Karena kedua garis dinyatakan sebagai persamaan vektor, kita akan mencari posisi relatif antara dua garis dengan metode satu titik dan satu vektor pada setiap garis.

Vektor arah setiap garis adalah:

$\vv{r} =(2,1,-3) \qquad \qquad \vv{s}=(0,5,1)$

Dan titik yang dimiliki setiap baris adalah:

$R(3,4,0)\qquad \qquad S(1,-2,2)$

Jadi, untuk menerapkan prosedur ini, pertama-tama perlu diperiksa apakah komponen-komponen vektor arah sebanding:

$\cfrac{2}{0} \neq \cfrac{1}{5} \neq \cfrac{-3}{1} \quad \longrightarrow \quad \text{No proporcionales}$

Karena kedua vektor tidak sebanding satu sama lain, maka garis hanya dapat berpotongan atau berpotongan. Oleh karena itu, sekarang kita perlu menyelesaikan determinan berikut yang terdiri dari vektor arah dan sebuah titik pada setiap garis:

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$

Kami mengganti nilainya ke dalam rumus:

$\begin{vmatrix} 2 & 0 & 3-1 \\[1.1ex] 1 & 5 & 4-(-2) \\[1.1ex]-3& 1 & 0-2 \end{vmatrix}$

Dan kami menghitung determinannya:

$\begin{vmatrix} 2 & 0 & 2 \\[1.1ex] 1 & 5 & 6 \\[1.1ex]-3& 1 & -2 \end{vmatrix}= 0$

Hasil determinannya setara dengan 0, sehingga garis-garisnya berpotongan .

Latihan 2

Hitung posisi relatif dua garis berikut:

$\displaystyle r: \ \begin{cases} x=3+2t \\[1.7ex] y=1+3t \\[1.7ex] z=2-t \end{cases} \qquad \qquad s: \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}$

lihat solusi

Baris pertama berbentuk persamaan parametrik dan baris kedua berbentuk persamaan kontinu, yang dengannya kita akan menentukan posisi relatif antara dua garis dari metode vektor satu titik setiap garis.

Koordinat vektor arah ke kanan

$r$

adalah koefisien di depan parameter

$t,$

dan koordinat vektor arah garis

$s$

adalah bilangan penyebutnya:

$\vv{r} =(2,3,-1) \qquad \qquad \vv{s}=(-4,-6,2)$

Dan titik yang dimiliki setiap baris adalah:

$R(3,1,2)\qquad \qquad S(-1,-5,4)$

Jadi, untuk menerapkan prosedur ini, pertama-tama perlu diperiksa apakah komponen-komponen vektor arah sebanding:

$\cfrac{2}{-4} = \cfrac{3}{-6}= \cfrac{-1}{2} \quad \longrightarrow \quad \text{Proporcionales}$

Kedua vektor tersebut sebanding satu sama lain, sehingga garis-garisnya hanya boleh sejajar atau berhimpitan. Untuk menghilangkan keraguan ini, perlu dilakukan substitusi titik pada garis

$r$

dalam persamaan garis

$s$

(atau sebaliknya) untuk melihat apakah memenuhi persamaan tersebut:

$R(3,1,2) \ \longrightarrow \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}$

$\cfrac{3+1}{-4}=\cfrac{1+5}{-6} = \cfrac{2-4}{2}$

$\cfrac{4}{-4}=\cfrac{6}{-6} = \cfrac{-2}{2}$

$-1=-1 = -1$

Dengan mensubstitusi titik pada garis kita memperoleh persamaan, sehingga titik pada satu garis memenuhi persamaan garis lainnya dan, terlebih lagi, vektor arahnya sebanding. Oleh karena itu, kedua garis tersebut berimpit.

Latihan 3

Temukan posisi relatif dari dua garis berikut:

$\displaystyle r: \ \begin{cases}2x-2y-2z+5=0 \\[2ex] 2x-y-1=0 \end{cases}$

$\displaystyle s: \ \begin{cases}4x-y+2z+3=0 \\[2ex] x-2y-3z+6=0 \end{cases}$

lihat solusi

Kedua garis tersebut merupakan bentuk persamaan umum (atau tersirat), jadi kita akan menggunakan metode rank untuk mencari posisi relatif antara kedua garis tersebut. Oleh karena itu kita buat matriks A dan matriks diperluas A’ dengan koefisien garis-garisnya:

$\displaystyle A=\begin{pmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3\end{pmatrix} \qquad \qquad A'=\begin{pmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{pmatrix}$

Setelah kita memiliki kedua matriks, kita perlu menghitung rank masing-masing matriks. Pertama kita hitung rank matriks A berdasarkan determinannya:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0$

$\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0$

$\displaystyle \begin{vmatrix}2 & -2 \\[1.1ex]2 & -1 \end{vmatrix}=2 \neq 0$

$rg(A)=2$

Semua determinan 3×3 pada matriks A adalah nol, tetapi terdapat determinan 2×2 yang bukan nol di dalam matriks tersebut, sehingga matriks A mempunyai rank 2 .

Dan sekarang kita menghitung ruang lingkup matriks A’ yang diperluas. Matriks A’ paling sedikit selalu merupakan range dari matriks A yang dalam hal ini adalah 2, sehingga perlu dicek apakah matriks tersebut mempunyai determinan 3×3 yang tidak menghilangkan dan juga berapa determinan dari matriks tersebut. seluruh matriks:

$rg(A')= \ ?$

$\displaystyle \displaystyle \begin{vmatrix}2 & -2 & 5\\[1.1ex]2 & -1 &-1\\[1.1ex]4 & -1 &3\end{vmatrix}=22 \neq 0$

$\displaystyle det(A')=\begin{vmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{vmatrix}=0$

$rg(A')=3$

Matriks A’ yang diperluas memang mengandung subdeterminan bukan nol 3×3 dan terlebih lagi determinan seluruh matriks yang diperluas sama dengan 0, sehingga matriks A’ mempunyai rangking 3 .

Jadi matriks A mempunyai rangking 2 dan matriks A’ mempunyai rangking 3, maka kedua garis tersebut sejajar . Artinya, mereka tidak mempunyai kesamaan.

$\color{orange} \boxed{\color{black} \quad rg(A) = 2 \neq rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Paralelas} \quad \vphantom{\Bigl(}}$

Ingatlah bahwa dalam penjelasan metode (di atas) Anda mempunyai tabel yang merangkum semua kemungkinan kasus posisi relatif antara dua garis menurut pangkat matriks A dan A’.

Latihan 4

Temukan posisi relatif dari dua garis berikut:

$\displaystyle r: \ \begin{cases}4x-y+2z=0 \\[2ex] x+y+3z-1=0 \end{cases}$

$\displaystyle s: \ \begin{cases}2x+5y-z-2=0 \\[2ex] 2x+3z+1=0 \end{cases}$

lihat solusi

Dalam hal ini, kedua garis tersebut berbentuk persamaan Kartesius (atau implisit), jadi kita akan menggunakan metode pengurutan untuk mencari posisi relatif antara kedua garis tersebut. Oleh karena itu, kita membuat matriks A dan matriks perluasan A’ dengan koefisien garis:

$\displaystyle A=\begin{pmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{pmatrix}$

Setelah kita mengetahui kedua matriks tersebut, kita perlu menghitung rank masing-masing matriks. Pertama-tama kita akan menghitung rank matriks A berdasarkan determinannya:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1 \end{vmatrix} = -65 \bm{\neq 0}$

$rg(A)=3$

Matriks A memuat submatriks berukuran 3×3 yang determinannya bukan nol, sehingga matriks A mempunyai rangking 3 .

Dan sekarang kita menghitung ruang lingkup matriks A’ yang diperluas. Matriks A’ paling sedikit akan selalu mempunyai rangking dari matriks A, yang dalam hal ini bernilai 3, jadi cukup diperiksa apakah matriks tersebut mempunyai rangking 4 atau rangking 3. Untuk melakukannya, kita selesaikan determinan dari himpunan matriks 4×4 dengan penjumlahan (atau kofaktor):

$rg(A')= \ ?$

$\displaystyle det(A')=\begin{vmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{vmatrix} =$

$\displaystyle =4 \cdot\begin{vmatrix} 1 & 3&-1\\[1.1ex] 5 & -1&-2\\[1.1ex] 0 & 3 &1 \end{vmatrix}-(-1)\cdot\begin{vmatrix}1 & 3&-1\\[1.1ex]2 & -1 & -2\\[1.1ex]2 & 3 &1 \end{vmatrix}+2\cdot\begin{vmatrix}1 & 1 &-1\\[1.1ex]2 & 5 & -2\\[1.1ex]2 & 0 &1 \end{vmatrix}-0\cdot \begin{vmatrix}1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{vmatrix}$

$\displaystyle =4 \cdot(-25)+1\cdot(-21)+2\cdot 9$

$\displaystyle =-100-21+18$

$\displaystyle =-103\bm{\neq0}$

$rg(A')=4$

Penentu seluruh matriks yang diperluas adalah bukan nol, sehingga matriks A’ mempunyai rangking 4 .

Sehingga matriks A mempunyai rangking 3 dan sebaliknya matriks A’ mempunyai rangking 4, maka kedua garis tersebut berpotongan di satu titik.

$\color{orange} \boxed{\color{black} \quad rg(A) = 3 \neq rg(A')= 4 \quad \longrightarrow \quad \text{Rectas se cruzan} \quad \vphantom{\Bigl(}}$

Ingatlah bahwa dalam penjelasan prosedur (di atas) Anda mempunyai tabel yang berisi semua kemungkinan kasus posisi relatif antara dua garis menurut pangkat matriks A dan A’.

Berapakah kedudukan relatif dua garis dalam ruang?

Menentukan kedudukan relatif dua garis dari suatu titik dan suatu vektor

Contoh penentuan posisi relatif antara dua garis

Temukan posisi relatif dua baris demi baris

Contoh cara mencari posisi relatif dua garis berdasarkan rentang

Menyelesaikan masalah kedudukan relatif antara dua garis dalam ruang

Latihan 1

Latihan 2

Latihan 3

Latihan 4

Tinggalkan Komentar Batalkan Balasan