Halaman ini menjelaskan perbedaan posisi relatif yang ada antara garis dan lingkaran. Selain itu, Anda juga dapat melihat cara mencari posisi relatif antara garis dan lingkaran.
Berapakah kedudukan relatif garis dan lingkaran?
Dalam geometri analitik, posisi relatif suatu garis terhadap lingkaran hanya dapat bersifat eksterior, garis singgung, atau garis potong:
- Bagian Luar : bila jarak antara garis dan pusat lingkaran lebih besar dari jari-jarinya.
- Garis singgung : bila jarak antara garis dan pusat lingkaran sama dengan jari-jarinya.
- Garis potong : bila jarak antara garis dan pusat lingkaran lebih kecil dari jari-jarinya.
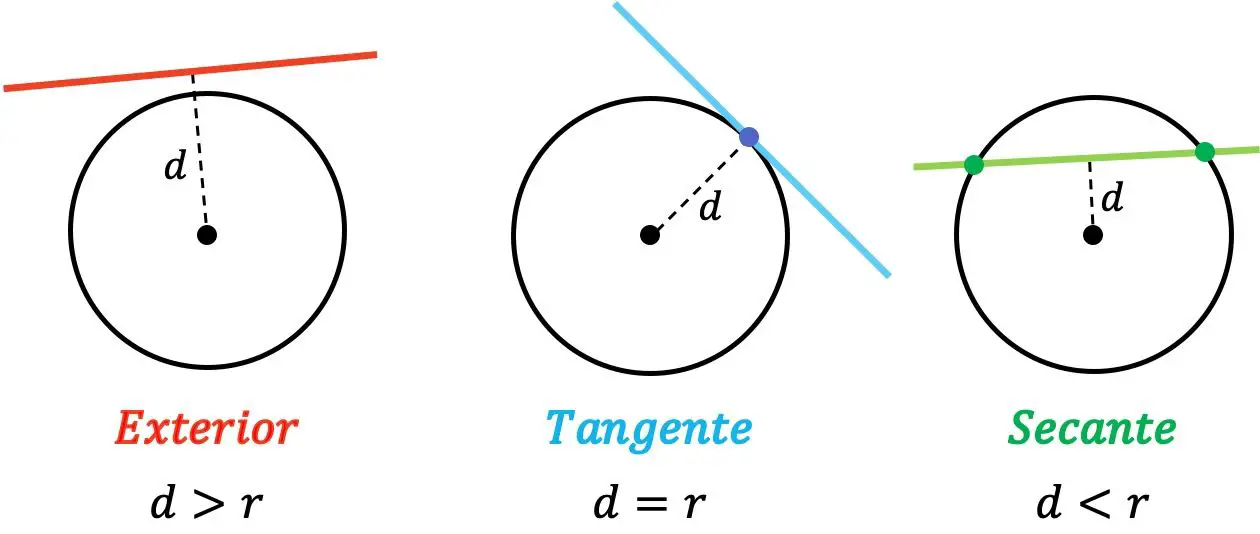
Jadi, jika suatu garis berada di luar lingkaran, maka garis tersebut tidak memotongnya di titik mana pun. Sebaliknya, jika garis bersinggungan dengan lingkaran, maka keduanya mempunyai titik yang sama. Dan terakhir, sebuah garis dipotong pada sebuah lingkaran jika garis tersebut memotongnya di dua titik berbeda.
Bagaimana cara menentukan kedudukan relatif antara garis dan lingkaran?
Ada dua cara untuk mencari posisi relatif suatu garis terhadap lingkaran pada bidang: satu dengan menghitung jarak antara garis dan pusat lingkaran, dan yang lainnya dengan menyelesaikan sistem persamaan gabungan dari persamaan garis dan persamaan lingkaran.
Selanjutnya, kita akan melihat secara pasti masing-masing metode tersebut.
Cara 1: Jarak antara garis dan pusat lingkaran
Seperti yang kita lihat pada penjelasan konsep kedudukan relatif antara garis dan lingkaran, jarak antara garis dan pusat lingkaran menunjukkan jenis kedudukan relatifnya.
Oleh karena itu, metode ini terdiri dari mencari jarak antara garis dan pusat lingkaran. Tentunya untuk dapat melakukannya anda harus mengetahui cara menghitung jarak antara titik dan garis , di halaman ini anda dapat melihat cara melakukannya, serta contoh dan latihan soal untuk latihan.
Jadi, tergantung pada hasil jarak yang diperoleh, hal itu akan terjadi dalam satu atau lain kasus:
- Garis akan berada di luar lingkaran jika jarak yang didapat lebih besar dari jari-jari lingkaran.
- Garis akan bersinggungan dengan lingkaran jika jarak yang diperoleh sama dengan jari-jari lingkaran.
- Garis akan memotong lingkaran jika jarak yang didapat lebih kecil dari jari-jari lingkaran.
Metode 2: selesaikan sistem persamaan
Cara lain untuk mencari kedudukan relatif suatu garis terhadap lingkaran adalah dengan menggunakan sistem persamaan yang dibentuk oleh persamaan garis dan persamaan lingkaran. Tentunya untuk menerapkan cara ini Anda perlu mengetahui apa itu persamaan keliling dan apa rumus persamaan garisnya .
Bergantung pada jumlah solusi sistem persamaan, kita akan dihadapkan pada satu kasus atau lainnya:
- Jika sistem persamaan tidak mempunyai penyelesaian berarti garis dan lingkaran tidak mempunyai titik persekutuan, sehingga garis berada di luar lingkaran.
- Jika sistem persamaan mempunyai 1 penyelesaian, berarti garis dan lingkaran mempunyai titik yang sama, sehingga garis tersebut bersinggungan dengan lingkaran.
- Jika sistem persamaan mempunyai 2 penyelesaian, berarti garis dan lingkaran mempunyai dua titik yang sama, sehingga garis tersebut memotong lingkaran.