Apa itu pemfaktoran polinomial? Ini adalah teknik matematika yang memungkinkan Anda menguraikan polinomial menjadi faktor atau ekspresi yang lebih sederhana. Dan berkat penyederhanaan ini, kita akan dapat melakukan operasi antara beberapa ekspresi aljabar dengan lebih mudah dan nyaman. Jadi, sepanjang artikel ini, kita akan membahas berbagai metode pemfaktoran polinomial dan semua kemungkinan kasus faktorisasi.
Bagaimana cara memfaktorkan polinomial?
Ada banyak metode faktorisasi yang memiliki struktur penyelesaiannya sendiri, namun pada akhirnya mengandalkan hal yang sama. Selain itu, Anda juga dapat menemukan berbagai macam kasus mengenai konfigurasi polinomial. Itu sebabnya pada bagian berikut ini kita akan membahas semua prosedur yang ada dan kapan harus menggunakan masing-masing prosedur tersebut. Terakhir, kami akan menerapkannya pada contoh nyata sehingga Anda selesai memperoleh konsepnya.
Faktorkan polinomial dengan aturan Ruffini
Metode pemfaktoran polinomial yang paling banyak digunakan adalah aturan Ruffini , karena mudah digunakan dan hasilnya dapat diketahui dengan cepat. Hal yang normal adalah menggunakan teknik ini untuk memfaktorkan polinomial yang berderajat lebih besar dari dua, atau bahkan terkadang memfaktorkan polinomial berderajat kedua. Karena ini memungkinkan Anda mendapatkan akar polinomial ini dengan sangat grafis. Meskipun penggunaan ini akan dijelaskan pada bagian selanjutnya yang berfokus pada akar ekspresi matematika jenis ini.
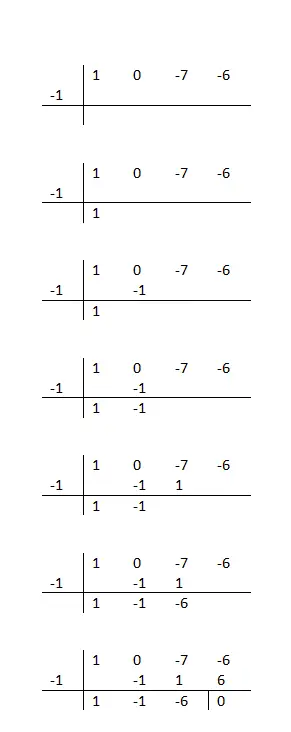
Bagaimana cara Ruffini memfaktorkan polinomial?
Pada dasarnya, kita harus menuliskan koefisien pembagian dalam garis horizontal dan nilai kemungkinan akar polinomial di sisinya. Kita katakan mungkin, karena kita harus mencari pembagi yang memungkinkan kita memperoleh sisa sama dengan nol. Jika tidak, nomor ini tidak akan menjadi root yang valid dan Anda harus terus mencoba.
Sebagai tip, kami menyarankan Anda hanya mencoba bilangan pembagi suku independen (nilai terakhir garis horizontal). Nah, untuk mengetahui apakah angka yang Anda pilih sudah benar, Anda hanya perlu mengikuti urutan perhitungan berikut ini :
Anda mengurangi koefisiennya, mengalikannya dengan akar yang Anda uji, menuliskannya di bawah koefisien berikutnya, dan melakukan penjumlahan vertikal. Anda hanya perlu mengulangi langkah-langkah ini sampai akhir, dan setelah selesai, Anda akan mengetahui apakah nilai ini benar atau tidak. Karena hanya bilangan yang mempunyai sisa nol yang valid.
Jika prosedur matematika yang perlu Anda ikuti kurang jelas bagi Anda, Anda dapat melihat contoh di kolom sebelah kiri teks ini. Selain itu, kami menyarankan Anda mencoba memfaktorkan polinomial berikut: x³ + 2x² – x – 2 (berdasarkan contoh). Dan terakhir, untuk mengetahui apakah Anda telah menyelesaikan latihan dengan benar atau tidak, Anda dapat membandingkan hasil Anda dengan yang ini:
- Ekspresi berlebih = x² + 3x + 2
- sisa = 0
Sekarang kami akan menjelaskan secara singkat penerapan Ruffini dalam faktorisasi . Meskipun jika Anda ingin mengetahui bagaimana sumber daya matematika ini digunakan secara detail, kami menyarankan Anda mengakses artikel terakhir yang kami tautkan, karena semuanya dijelaskan dengan sangat baik di sana. Oleh karena itu, mari kita mulai dengan menjelaskan cara memfaktorkan polinomial dengan aturan Ruffini:
- Kami menggambar grid: seperti yang bisa kita lihat pada gambar di atas, kita akan membuat kotak di mana kita akan membuat Ruffini. Pada dasarnya, Anda harus menulis koefisien ekspresi yang diurutkan secara horizontal dan tanpa menyisakan nilai nol. Pada akhirnya, Anda harus memiliki representasi yang mirip dengan gambar tetapi dengan nilai polinomial Anda.
- Kami menghitung akar-akarnya: setelah kami menggambar strukturnya dan memastikan bahwa semua bilangan ditulis dengan benar, kami akan melanjutkan untuk menghitung akarnya. Anda perlu mencari akar-akarnya dengan mengikuti urutan perhitungan yang kita bicarakan tepat di atas daftar ini (dengan gambar).
- Kita menyatakan akar dalam bentuk (x – a): jika kita memiliki semua akar polinomial maka kita harus menyatakannya dalam bentuk berikut (x – a). Mengingat a adalah nilai yang kita peroleh, misal kita ekstrak hasilnya x = 2, x = -2 dan x = 4, maka kita peroleh (x – 2), (x + 2) dan ( x – 4).
- Kita mengumpulkan semua faktor dalam satu ekspresi: terakhir, ketika kita sudah memiliki semua akar yang dinyatakan dalam format yang benar, kita tinggal mengumpulkannya dalam satu ekspresi aljabar. Melanjutkan contoh sebelumnya, kita akan mendapatkan sesuatu seperti ini: (x – 2) · (x + 2) · (x – 4).
Faktorkan polinomial menggunakan akar-akar polinomial
Kami telah menjelaskan setengah konsep akar polinomial di bagian Ruffini. Namun, definisi pastinya adalah: akar polinomial P(x) adalah nilai numerik a, sehingga P(a) = 0 . Oleh karena itu, bilangan tersebut mampu menghilangkan fungsi atau polinomial yang bersangkutan. Singkatnya, kita dapat mengatakan bahwa ini digunakan untuk menguraikan polinomial menjadi produk faktor.
Misalnya, jika kita diberikan persamaan berikut x² − x − 2 dan kita memfaktorkannya menggunakan aturan Ruffini atau hanya dengan menyelesaikan persamaan kuadrat x² − x − 2 = 0. Kita akan memperoleh dua nilai x = -1 dan x = 2, jadi jika kita mengubahnya ke format (x – a) dan menyatukannya, kita akan mendapatkan persamaan berikut: (x + 1) (x − 2), yaitu polinomial terfaktor . Dan kita dapat menerapkan ini pada polinomial yang derajatnya lebih besar dari dua, meskipun ekspresi tersebut terdiri dari lebih dari satu suku.
Memfaktorkan polinomial dengan ekstraksi faktor persekutuan
Jika kita ingin memfaktorkan polinomial tanpa suku bebas atau ekspresi yang memiliki faktor persekutuan di semua suku, maka kita dapat menyederhanakan polinomial tersebut menggunakan teknik ini. Ini pada dasarnya melibatkan penerapan properti distributif ke seluruh ekspresi, menghilangkan faktor persekutuan berulang dan menambahkannya dengan mengalikan seluruh polinomial. Di bawah ini Anda akan menemukan contoh kasus pertama yang kita bicarakan (polinomial tanpa suku independen):
2x³ + 10x² – 6x = 2x (x² + 5x – 3)
Ekstraksi ganda dari faktor persekutuan
Ekstraksi faktor persekutuan bahkan dapat dilakukan dengan mengekstraksi faktor yang lebih kompleks, yang mencakup banyak variabel. Dan Anda bahkan dapat mengekstrak polinomial yang berasal dari ekspresi utama itu sendiri. Penting untuk tidak menetapkan batasan saat Anda ingin melakukan operasi jenis ini, karena tujuan ekstraksi faktor adalah untuk menyederhanakan ekspresi aljabar sebanyak mungkin .
Memfaktorkan polinomial menggunakan identitas penting
Produk penting dapat membantu kita memfaktorkan ekspresi polinomial, karena ini adalah ekspresi aljabar yang disederhanakan. Oleh karena itu, rumus tersebut membantu kita beralih langsung dari polinomial panjang ke rumus kecil yang terdiri dari beberapa suku. Oleh karena itu sangat disarankan untuk mempelajari rumus-rumus identitas penting agar dapat dengan cepat mengidentifikasi kapan Anda dapat menggunakannya. Dan oleh karena itu menghemat waktu kita untuk melakukan anjak piutang dengan Ruffini atau metode lainnya. Selanjutnya, kami akan membahas tiga aturan yang perlu Anda pelajari:
- Selisih kuadrat: a² – b² = (a + b) · (a – b)
- Kuadrat jumlahnya: a² + 2ab + b² = (a + b)²
- Pengurangan kuadrat: a² – 2ab + b² = (a – b)²
Memfaktorkan polinomial dengan mengelompokkan
Dalam beberapa kasus kita dapat menemukan polinomial dengan struktur x² – ax – bx + ab , yang dapat disederhanakan dengan menghilangkan faktor persekutuan: x (x – a) – b (x – a). Dan jika kita mengambil faktor persekutuannya lagi, maka dapat disederhanakan lagi: (x – a) · (x – b). Oleh karena itu, akar-akar polinomial ini adalah x = a dan x = b. Seperti yang Anda lihat, ekspresi aljabar jenis ini memiliki struktur yang sangat mudah untuk difaktorkan dan digunakan.
Latihan faktorisasi polinomial
Terakhir, kami ingin menawarkan serangkaian latihan agar Anda dapat berlatih memfaktorkan polinomial. Dengan cara ini Anda akan dapat menginternalisasikan teori yang telah kami jelaskan hari ini dengan lebih baik. Sederhananya, Anda harus menyelesaikan latihan di buku catatan Anda dan kemudian membandingkan hasilnya dengan yang kami tawarkan di bawah ini.
- x 4 -1 = (x 2 + 1) (x + 1) (x – 1)
- x 5 + x 4 – x – 1 = (x – 1) (x + 1) 2 (x 2 + 1)
- 9×2 + 30x + 25 = (3x + 5) 2
- x 4 – 3x 3 – 3x 2 + 11x – 6 = (x + 2) (x – 3) (x – 1) 2