Polinomial

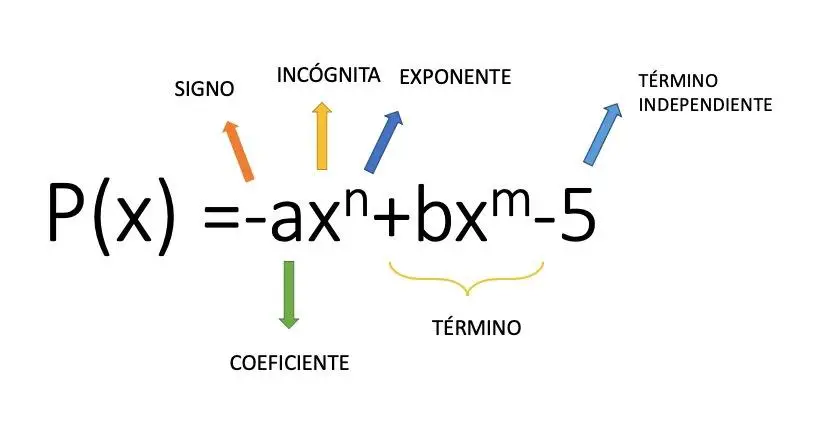
Monomial adalah ekspresi aljabar yang dibentuk oleh koefisien (nilai numerik) yang mengalikan suatu variabel dengan eksponen, misalnya ekspresi 4x² adalah monomial. Maka dari konsep matematika ini kita sampai pada polinomial yang merupakan himpunan penjumlahan dan pengurangan beberapa monomial. Pada gambar di atas Anda dapat melihat contoh struktur polinomial yang terdiri dari beberapa monomial.

jenis polinomial

Melalui eksponen monomial tertentu, kita dapat mengklasifikasikan polinomial menjadi beberapa jenis. Kita dapat mengklasifikasikan ekspresi ini ke dalam kategori seperti: polinomial derajat pertama, polinomial derajat kedua, polinomial derajat ketiga, dan seterusnya. Pada dasarnya, Anda perlu mengidentifikasi monomial yang memiliki eksponen terbesar dan yang akan menjadi derajat polinomialnya . Dan begitu Anda mengetahuinya, Anda dapat mengklasifikasikannya menjadi salah satu jenis yang baru saja kita bicarakan.

Polinomial beberapa variabel

Selain itu, ada pula cara lain untuk menyusun polinomial, yaitu berdasarkan jumlah monomial yang membentuknya. Misalnya, jika kita memiliki binomial , maka ini setara dengan memiliki polinomial dengan dua suku, jika kita memiliki trinomial , ini setara dengan memiliki polinomial dengan tiga suku, dan seterusnya. Semua cara mengkatalogkan polinomial ini memiliki banyak subkategori yang tak terhingga banyaknya. Karena ekspresi ini dapat terdiri dari monomial apa pun yang kita inginkan dan juga dapat memiliki derajat apa pun.

Ciri-ciri dan sifat-sifat polinomial

• Derajat absolut suatu polinomial: Pada bagian sebelumnya, kita telah membahas definisi derajat relatif. Namun dalam kasus polinomial yang dibentuk oleh lebih dari satu variabel, kita mempunyai derajat absolut yang setara dengan jumlah maksimum eksponen semua variabel monomial tersebut. Misalnya, pada monomial 5x²y³, derajat absolutnya sama dengan 2 + 3 = 5.
• Polinomial terurut: Kita mendefinisikan polinomial terurut terhadap suatu variabel ketika eksponen variabel tersebut disusun dalam urutan menaik atau menurun. Misalnya, jika kita menemukan polinomial P(x) = 3x + 4x³ – x², dalam hal ini polinomial tersebut tidak akan diurutkan. Jadi, kita harus memperbaikinya dan kita akan mendapatkan hasil ini: P(x) = 4x³ – x² + 3x.
• Polinomial lengkap: Jika kita menemukan polinomial yang memiliki monomial dengan semua eksponen yang mungkin (dari derajat tertinggi hingga suku bebas), kita katakan bahwa polinomial tersebut adalah polinomial lengkap . Misalnya, ekspresi berikut: P(x) = 3 x² + 2x – 4 termasuk dalam tipe ini karena tidak ada eksponen yang hilang antara 2 dan 0.
• Polinomial homogen: adalah polinomial yang mempunyai derajat absolut yang sama pada setiap monomialnya. Variabel dapat memiliki nilai eksponen yang berbeda, tetapi jumlah eksponen variabel di semua monomial harus sama. Contoh: P(x) = x²y³z + 3 x ⁴ yz, hasil penjumlahan kedua adalah enam 2 + 3 + 1 = 4 + 1 + 1 = 6.
• Polinomial identik: Jika kita menemukan dua atau lebih polinomial yang memiliki koefisien suku-suku yang sama, maka kita akan mengatakan bahwa keduanya adalah polinomial identik. Di bawah ini Anda dapat melihat contoh antara dua polinomial: P(x) = 2x + 27 dan Q(x) = 5 (x + 3) – 3 (x – 4), keduanya identik karena koefisien masing-masing eksponennya sama : 2x = 5x – 3x dan 27 = 15 + 12.
• Polinomial nol: Polinomial ini hanya memiliki koefisien nol (sama dengan nol), sehingga nilai total polinomial tersebut juga akan menjadi nol. Polinomial P(x) = 0x³ + 0x² – 0x – 0 adalah contoh jelas dari jenis polinomial ini, namun jangan sampai tertukar dengan Q(x) = 0, karena dalam kasus ini Anda membentuk persamaan dan tidak tidak berarti semua koefisien Q(x) adalah 0.

Nilai numerik polinomial

Nilai numerik suatu polinomial adalah hasil yang diperoleh dengan mensubstitusi variabel ekspresi ini dengan suatu bilangan. Kita hanya perlu menyelesaikan polinomial ini seolah-olah ini adalah operasi gabungan . Selanjutnya, kami akan menjelaskan tiga metode yang dapat Anda gunakan untuk mendapatkan nilai numerik dari ekspresi seperti ini.

• Penggantian langsung: ketika kita diberikan secara langsung nilai yang sesuai dengan masing-masing variabel polinomial, kita cukup mengganti variabel tersebut dengan angka-angka tersebut. Dengan cara ini, jika kita mempunyai polinomial P(x) = 2x² – x + 4 dan diketahui bahwa x = 3, maka nilai numerik polinomial tersebut akan sama dengan 2 · 3² – 3 + 4 = 19.
• Resolusi variabel: kita akan menerapkan kasus ini ketika mereka tidak secara langsung memberi kita nilai variabel, namun memberi kita kesetaraan. Misalnya, P(2) jika P(x – 1) = x³ – 2x + 1 benar, maka kita selesaikan dulu persamaan 2 = x – 1 dan dapatkan x = 3. Terakhir, kita harus mensubstitusikan 3 ke x, sehingga 3³ – 2 · 3 + 1 = 22.
• Perubahan variabel: ketika kita memiliki polinomial P(x) = 4x – 2 dan kita ingin mengetahui nilai P(x + 2). Selanjutnya, kita perlu mengubah semua x dalam ekspresi menjadi a(x+2). Oleh karena itu, mari kita lihat seperti apa contoh penyelesaian terakhir ini: P (x + 2) = 4 (x + 2) – 2.

Operasi dengan polinomial

Di bawah ini kami akan menjelaskan cara menyelesaikan empat operasi aritmatika dasar dengan polinomial , selalu mengikuti hierarki operasi . Di setiap bagian Anda akan menemukan sedikit teori yang memungkinkan Anda mengetahui cara melanjutkan setiap kasus dan beberapa contoh praktis.

penjumlahan polinomial

Untuk menjumlahkan polinomial kita harus memperhitungkan fakta bahwa polinomial tersebut hanya dapat dikelompokkan berdasarkan suku-suku yang sejenis , jadi jika kita memiliki polinomial P(x) = 3x³ – x² + 2x – 4 dan Q(x) = 2x² + 3x – 2. Jadi untuk membuat P(x) + Q(x), kita jumlahkan koefisien kedua polinomial yang disertai eksponen yang sama: P(x) + Q(x) = 3x³ + (-x) ² + 2x²) + ( 2x + 3x) + (-4 -2) = 3x³ + x² + 5x – 6. Singkatnya, kita dapat mengatakan bahwa kita mengelompokkan dan menjumlahkan koefisien dari setiap suku yang serupa dan pada akhirnya kita menyatakan semua suku dalam satu polinomial .

pengurangan polinomial

Pengurangan polinomial diselesaikan dengan cara yang sama seperti penjumlahan, satu-satunya perbedaan adalah simbolnya. Kemudian kita mengelompokkan suku-suku serupa, mengurangi dan mengubah semuanya menjadi satu ekspresi. Di bawah ini kami tunjukkan menggunakan contoh: P(x) = 5x³ – 2x² + x – 3 dan Q(x) = 3x² + 5x + 4, maka P(x) – Q(x ) = 5x³ + (-2x² + 3x²) + (x + 5x) + (-3 + 4) = 5x³ + x² + 6x + 1.

perkalian polinomial

Saat menyelesaikan perkalian jenis ini, segalanya bisa menjadi sedikit rumit, tetapi jika Anda mengikuti semua langkah yang akan kami sampaikan kepada Anda, Anda akan baik-baik saja. Dalam operasi matematika ini semua monomial akan beroperasi dengan semua monomial lainnya, artinya kita tidak hanya akan mengalikan suku-suku serupa. Selain itu, tidak hanya koefisiennya yang berubah , eksponennya juga akan berubah . Dengan contoh ini Anda akan memahami semuanya dengan lebih baik: P(x) = 2x² + 3x – 1 dan Q(x) = 2x + 3:

P(x) Q(x) = ( 2x² + 3x –1 ) · ( 2x + 3 ) = 2x² · 2x + 2x² · 3 + 3x · 2x + 3x · 3 + (-1 ) · 2x + (-1 ) · 3 = 4x³ + 6x² + 6x² + 9x – 2x – 3 = 4x³ + 12x² + 7x – 3

Pada dasarnya, kita mengalikan koefisien setiap suku polinomial dengan semua suku kedua, lalu kita menerapkan sifat pangkat dari a ⁿ · ^am = a ^n+m .

pembagian polinomial

Terakhir, kita hanya perlu menjelaskan cara menyelesaikan pembagian polinomial, pada dasarnya kita perlu menerapkan sifat distributif pembagian: (a + b + c) ÷ d = (a ÷ d) + (b d) + (c −d). Dan kita juga akan menerapkan sifat eksponensial berikut pada ⁿ − ^am = a ^nm . Sekarang kita akan melihatnya dengan contoh sederhana: P(x) = 3x³ – 6x² + 9x dan Q(x) = 3x.

P(x) Q(x) = ( 3x³ – 6x² +9x ) 3x = ( 3x³ − 3x ) + ( 6x² − 3x ) + (9x − 3x ) = x² – 2x + 3

Sekarang setelah Anda selesai melihat cara menyelesaikan semua operasi dengan polinomial ini, kami harap Anda tahu cara menerapkannya dalam praktik. Namun jika menurut Anda bukan itu masalahnya dan Anda ingin terus berlatih sedikit, kami sarankan Anda melihat beberapa latihan yang dapat diselesaikan di halaman ini . Ini akan membantu Anda menyelesaikan internalisasi semua konsep matematika ini.

Memfaktorkan polinomial

Untuk memfaktorkan polinomial bisa dilakukan secara manual seperti yang sudah dijelaskan pada artikel di link terakhir ini atau bisa juga menggunakan kalkulator Ruffini . Kami merekomendasikan melakukannya dengan opsi kedua ini jika Anda ingin melakukannya dengan cepat, tetapi jika Anda baru belajar memfaktorkan, lebih baik Anda berlatih secara manual. Cara melakukan ini harus dipilih berdasarkan situasi Anda.

Selesaikan polinomial dengan kalkulator ilmiah

Ada banyak kalkulator ilmiah berbeda di pasaran saat ini. Namun jika Anda sedang mencari kalkulator murah yang bisa menyelesaikan polinomial , kami merekomendasikan Casio FX-991SPX II . Mudah digunakan, sangat kuat dan fungsional, membuatnya sempurna untuk siswa matematika sekolah menengah dan atas. Di bawah ini kami akan menjelaskan secara singkat bagaimana ekspresi matematika dari gaya ini diselesaikan menggunakan model Casio ini atau yang serupa.

Anda harus memasukkan nilai numerik variabel terlebih dahulu, tulis lalu tekan “STO” + huruf variabel , misalnya x. Jadi ketika semua variabel sudah terdefinisi, Anda hanya perlu menulis ekspresi polinomial sebagaimana adanya dengan semua variabel dan semua angkanya. Dan terakhir, Anda harus menekan tombol sama dengan, dengan cara ini Anda akan mendapatkan hasil yang setara dengan nilai numerik polinomial.