Persamaan garis singgung -

Pada artikel ini kita akan melihat cara mencari persamaan garis singgung suatu kurva. Selain itu, Anda dapat berlatih dengan latihan yang diselesaikan dengan tingkat kesulitan berbeda.

Persamaan garis singgung suatu fungsi di suatu titik

Persamaan garis singgung fungsi f(x) di titik x=x ₀ adalah:

$y -y_0= m(x-x_0)$

Dimana titik P(x ₀ ,y ₀ ) merupakan titik dimana garis singgung dan fungsinya berimpit. Dan kemiringan garis singgung, m, sama dengan turunan kurva di titik x ₀ , yaitu m=f'(x ₀ ).

Pada gambar di atas Anda dapat melihat sebuah kurva

$f(x)$

diwakili dengan warna biru dan garis oranye yang bersinggungan dengan fungsi tersebut

$f(x)$

Tentang

$x=x_0$

, karena mereka hanya memiliki kesamaan dalam hal ini. Nah, persamaan garis singgungnya adalah

$y -y_0= m(x-x_0)$

, dan kemiringannya adalah

$m=f'(x_0)$

Cara mencari persamaan tangen

Untuk mencari persamaan garis singgung suatu fungsi di suatu titik, Anda perlu melakukan:

Mencari kemiringan garis singgung dengan menghitung turunan fungsi di titik singgung tersebut.
Tentukan sebuah titik pada garis singgung tersebut.
Temukan persamaan garis singgung menggunakan perhitungan kemiringan dan titik garis singgung.

Contoh persamaan garis singgung suatu kurva

Setelah kita melihat teori persamaan tangen, mari kita lihat cara menghitung persamaan tangen dengan menyelesaikan contoh langkah demi langkah:

Hitung persamaan garis singgung kurva
$f(x)=x^2+x$

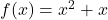
Tentang

$x=1$

.

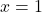
Kita tahu bahwa persamaan tangen selalu berbentuk berikut:

$y -y_0= m(x-x_0)$

Hal pertama yang harus dilakukan adalah menghitung kemiringan garis. Jadi, kemiringan garis singgung,

$m$

, akan menjadi nilai turunan kurva pada titik singgung x=1, yaitu

$m=f'(1).$

Maka dari itu kita bedakan fungsinya lalu kita hitung

$f'(1):$

$f(x)=x^2+x \quad \longrightarrow \quad f'(x)=2x+1$

$f'(1)= 2\cdot 1+1=2+1=3$

$m=f'(1)=3$

Setelah kita mengetahui nilai dari

$m$

, kita perlu menemukan suatu titik

$(x_0,y_0)$

garis singgung untuk melengkapi persamaan garis singgung.

Persamaan garis singgung dan kurva selalu mempunyai titik persekutuan , yang dalam hal ini adalah

$x=1$

. Oleh karena itu, seperti kurva

$f(x)$

melewati titik ini, kita dapat mencari komponen titik lainnya dengan menghitung

$f(1):$

$f(x)=x^2+x$

$f(1)=1^2+1=2$

Oleh karena itu, titik singgungnya adalah:

$P(1,2)$

Baik kurva maupun garis singgung melewati titik ini, jadi kita juga dapat menggunakannya untuk mencari persamaan garis singgung.

Yang tersisa hanyalah mengganti nilai kemiringan dan titik singgung yang ditemukan ke dalam persamaannya:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=3 \qquad P(1,2) \end{array} \right\} \longrightarrow \ y -2= 3(x-1)$

Singkatnya, persamaan tangennya adalah:

$\bm{y-2=3(x-1)}$

Anda juga dapat menyatakan persamaan garis singgung dengan persamaan garis eksplisit:

$\bm{y=3x-1}$

Di bawah ini Anda dapat melihat kurva yang diwakili

$f(x)=x^2+x$

dan garis singgungnya

$x=1,$

$y-2=3(x-1):$

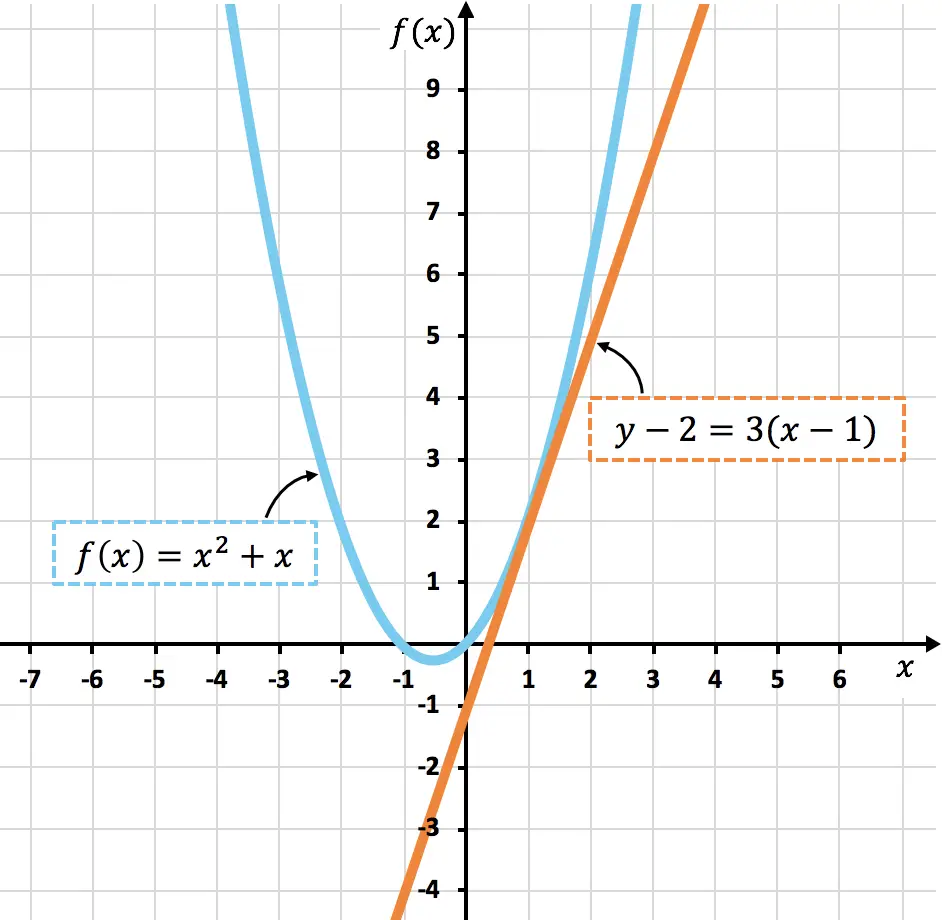
persamaan garis singgung kurva di suatu titik

Seperti yang Anda lihat, kurvanya

$f(x)=x^2+x$

dan garis singgung

$y-2=3(x-1)$

mereka hanya mempunyai kesamaan maksudnya

$(1,2)$

, persis seperti yang kami hitung.

Latihan soal persamaan tangen diselesaikan

Latihan 1

Hitung persamaan garis singgung kurva

$f(x)=2x^2-4x+3$

Tentang

$x=2 .$

Lihat solusinya

Persamaan tangen akan selalu berbentuk berikut:

$y-y_0=m(x-x_0)$

Langkah 1: Hitung kemiringan garis singgung

Kemiringan, m , adalah nilai turunan kurva di titik singgung. Oleh karena itu, dalam hal ini

$m = f'(2):$

$f(x)=2x^2-4x+3 \ \longrightarrow \ f'(x)= 4x-4$

$f'(2)= 4\cdot 2-4=8-4=4$

$m=f'(2)=4$

Langkah 2: Temukan titik pada garis singgung

Persamaan garis singgung dan kurva selalu mempunyai titik persekutuan, yang dalam hal ini adalah

$x=2$

. Oleh karena itu, seperti kurva

$f(x)$

melewati titik ini, kita dapat mencari komponen titik lainnya dengan menghitung

$f(2):$

$f(x)=2x^2-4x+3$

$f(2)=2\cdot 2^2-4\cdot 2+3 =2 \cdot 4 -8 +3 = 3$

Jadi, titik yang dilalui kurva dan garis singgung adalah titik

$(2,3).$

Langkah 3: Tulis persamaan tangennya

Yang tersisa hanyalah mengganti nilai kemiringan dan titik singgung yang ditemukan ke dalam persamaannya:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(2,3) \end{array} \right\} \longrightarrow \ y -3= 4(x-2)$

Oleh karena itu, persamaan tangennya adalah:

$\bm{y -3= 4(x-2)}$

Latihan 2

Hitung persamaan garis singgung kurva

$\displaystyle f(x)=-3x^2+2x$

di titik asal koordinat.

Lihat solusinya

Asal koordinat mengacu pada titik

$(0,0).$

Oleh karena itu kita harus menghitung garis singgung fungsi tersebut di titik tersebut

$(0,0) .$

Pertama, kita menentukan nilai kemiringan garis singgung dengan menghitung turunan di titik asal koordinat:

$f(x)=-3x^2+2x \ \longrightarrow \ f'(x)= -6x+2$

$f'(0)= -6\cdot 0+2=2$

$m=f'(0)=2$

Dalam hal ini, kita sudah mengetahui titik yang dilalui garis singgung. Karena pernyataan tersebut menyatakan bahwa garis tersebut harus bersinggungan dengan kurva di titik asal, yaitu di titik

$(0,0).$

Jadi titik dimana kurva dan garis singgungnya adalah titik

$(0,0).$

Terakhir, substitusikan nilai kemiringan dan titik singgung yang ditemukan ke dalam persamaan Anda:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=2 \qquad P(0,0) \end{array} \right\} \longrightarrow \ y -0= 2(x-0)$

Kesimpulannya, persamaan tangennya adalah:

$y -0= 2(x-0)$

$\bm{y = 2x}$

Latihan 3

Hitung garis singgung kurva tersebut

$f(x)=x^2-2x-1$

yang sejajar dengan kanan

$y-4x-6=0$

Lihat solusinya

Dalam soal ini kita diberitahu bahwa garis singgung harus sejajar dengan garis

$y-4x-6=0 .$

Dan dua garis dikatakan sejajar jika mempunyai kemiringan yang sama. Oleh karena itu, garis singgung harus mempunyai kemiringan yang sama dengan garis

$y-4x-6=0.$

Artinya kita perlu mencari kemiringan garis

$y-4x-6=0 .$

Untuk melakukan ini, kami menghapus variabel dan:

$y-4x-6=0 \ \longrightarrow \ y =4x+6$

Jadi kemiringan garisnya

$y=4x+5$

adalah 4, karena kemiringan suatu garis adalah bilangan yang mengalikan x jika ynya jelas.

Oleh karena itu kemiringan garis singgungnya juga harus 4, karena agar sejajar harus mempunyai kemiringan yang sama.

$m=4$

Dalam hal ini mereka tidak memberitahu kita titik singgung antara kurva dan garis singgung. Namun kita mengetahui bahwa turunan kurva pada titik singgung sama dengan kemiringan garis singgung, yaitu

$m=f'(x_0)$

. Nah bagaimana kita bisa mengetahui nilainya

$m$

, kita dapat mencari x ₀ dari persamaan tersebut

$m=f'(x_0):$

Untuk melakukan ini, pertama-tama kita menghitung turunan dari

$f(x):$

$f(x)= x^2-2x-1 \ \longrightarrow \ f'(x)=2x-2$

Dan sekarang kita menyelesaikannya

$m=f'(x_0)$

mengetahui bahwa

$m = 4 :$

$m =f'(x_0)$

$4 =2(x_0)-2$

$4+2 =2x_0$

$6 =2x_0$

$\cfrac{6}{2} =x_0$

$3=x_0$

Dan setelah kita mengetahui koordinat x suatu titik, kita dapat mencari koordinat titik lainnya dengan menghitung

$f(3):$

$f(3)=3^2-2\cdot 3-1= 9-6-1=2$

Jadi, titik yang dilalui kurva dan garis singgung adalah titik

$(3,2).$

Yang tersisa hanyalah mengganti nilai kemiringan dan titik singgung yang ditemukan ke dalam persamaannya:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(3,2) \end{array} \right\} \longrightarrow \ y -2= 4(x-3)$

Dan persamaan garis singgungnya adalah:

$\bm{y -2=4(x-3)}$

Latihan 4

Hitung garis singgung kurva tersebut

$f(x)=2x^2+5x+1$

yang membentuk sudut 45º dengan sumbu X.

Lihat solusinya

Rumusan masalah memberitahu kita bahwa garis singgung harus membentuk sudut 45º terhadap sumbu X. Dalam kasus ini, rumus berikut harus diterapkan untuk mencari nilai kemiringan:

$m = \text{tg}\left(\alpha\right)$

$m = \text{tg}\left(45^{\text{o}}\right) = 1$

Pernyataan tersebut tidak menentukan titik singgung antara kurva dan garis singgung. Namun kita mengetahui bahwa turunan kurva pada titik singgung sama dengan kemiringan garis singgung, yaitu

$m=f'(x_0)$

. Oleh karena itu, kita dapat menghitung x ₀ dengan menyelesaikan persamaan tersebut

$m=f'(x_0):$

Untuk melakukan ini, pertama-tama kita menghitung turunan dari

$f(x):$

$f(x)=2x^2+5x+1\ \longrightarrow \ f'(x)=4x+5$