Di sini Anda akan menemukan penjelasan tentang apa itu rumus persamaan garis kanonik (atau segmental) yang disebut juga persamaan simetris. Selain itu, Anda akan dapat melihat contoh dan latihan dengan latihan yang diselesaikan. Dan, bahkan, Anda akan menemukan bagaimana persamaan kanonik dihitung dari persamaan garis umum (atau implisit).
Apa persamaan garis kanonik atau segmental?
Ingatlah bahwa definisi matematis garis adalah sekumpulan titik berurutan yang direpresentasikan dalam arah yang sama tanpa kurva atau sudut.
Jadi, persamaan garis kanonik , juga disebut persamaan segmental garis , adalah cara untuk menyatakan garis apa pun secara matematis. Untuk melakukannya, cukup mengetahui titik potong dengan sumbu koordinat garis tersebut.
Sebaliknya, dalam geometri analitik, persamaan garis kanonik (atau segmental) disebut juga persamaan garis simetris .
Rumus persamaan garis kanonik atau segmental
Persamaan garis kanonik atau segmental adalah ekspresi aljabar garis yang dapat ditentukan dengan mengetahui nilai perpotongan garis tersebut dengan sumbu x dan sumbu y.
Jika sebuah garis memotong sumbu kartesius di titik-titik berikut:
Titik potong dengan sumbu X:
![]()
Titik potong dengan sumbu Y:
![]()
Rumus persamaan garis kanonik (atau segmental) adalah:
![]()

Perlu dicatat bahwa tidak ada persamaan garis kanonik (atau segmental) dalam salah satu dari tiga kasus berikut:
- Jika garisnya vertikal, artinya sejajar dengan sumbu OY. Karena persamaan garis vertikal adalah

- Bila garisnya mendatar, artinya sejajar dengan sumbu OX. Karena persamaan garis mendatar adalah

- Ketika garis melewati titik asal koordinat (titik
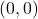
), karena kita akan mempunyai dua ketidakpastian dalam persamaan garis.
Contoh cara mencari persamaan garis kanonik atau segmental
Agar Anda lebih memahami konsepnya, kami akan menyelesaikan masalah persamaan garis segmental (atau kanonik):
- Tentukan persamaan kanonik atau segmental garis yang melalui dua titik berikut:
![]()
Dalam hal ini, deklarasi tidak memberi kita 2 titik, melainkan dua titik perpotongan dengan sumbu.
Titik potong garis dengan sumbu X:
![]()
Titik potong garis dengan sumbu Y:
![]()
Jadi, karena kita sudah mengetahui dua titik potong dengan sumbunya, kita tinggal menerapkan rumus persamaan garis kanonik atau segmental:
![]()
Dan terakhir, kami mengganti nilai parameternya
![]()
Dan
![]()
dalam rumus:
![]()
Anda sekarang tahu apa persamaan garis kanonik (atau segmental). Namun, Anda harus tahu bahwa ada cara lain untuk menyatakan suatu garis, dan di antaranya adalah persamaan eksplisit yang menonjol. Jenis persamaan garis ini sulit untuk dipahami sepenuhnya, jadi kami telah menjelaskan semuanya secara rinci di halaman tertaut.
Hitung persamaan garis kanonik atau segmental dari persamaan umumnya
Kita baru saja melihat cara menentukan persamaan garis kanonik atau segmental, tetapi ada juga metode lain:
Persamaan kanonik atau segmental suatu garis dapat diperoleh dari persamaan umum (atau implisit) garis yang sama:
![]()
Pertama, kita berpindah sisi pada koefisien C:
![]()
Selanjutnya, kita membagi seluruh persamaan dengan nilai parameter C yang berubah tanda:
![]()
![]()
Dan, melalui sifat-sifat pecahan, kita sampai pada rumus persamaan garis kanonik atau segmental:
![]()
Oleh karena itu, dari rumus ini istilahnya
![]()
Dan
![]()
persamaan kanonik suatu garis setara dengan ekspresi berikut:
![]()
Memecahkan masalah persamaan garis kanonik atau segmental
Latihan 1
Berapakah titik potong dengan sumbu koordinat garis berikut?
![]()
Garis dalam latihan dinyatakan dalam bentuk persamaan garis kanonik atau segmental, yang rumusnya adalah:
![]()
Oleh karena itu, titik potong garis terhadap sumbu koordinat adalah:
Titik potong dengan sumbu X:
![]()
Titik potong dengan sumbu Y:
![]()
Latihan 2
Apa persamaan kanonik atau segmental dari garis grafik?
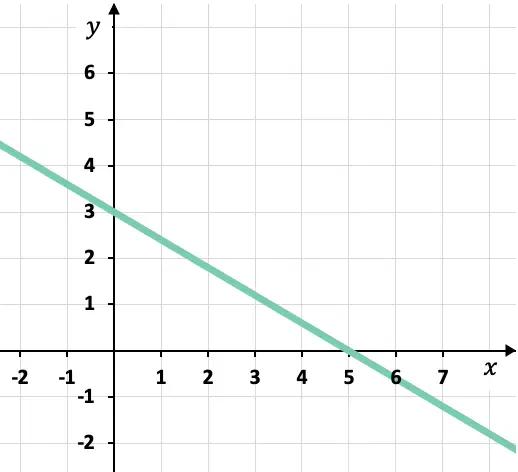
Dari grafik tersebut kita dapat mengetahui titik-titik perpotongan garis dengan sumbu koordinat:
Titik potong garis dengan sumbu X:
![]()
Titik potong garis dengan sumbu Y:
![]()
Jadi, setelah kita mengetahui 2 titik potong sumbunya, kita tinggal menggunakan rumus persamaan garis kanonik atau segmental:
![]()
Dan terakhir, kami mengganti nilai parameternya
![]()
Dan
![]()
dalam rumus:
![]()
Latihan 3
Hitung persamaan kanonik atau segmental garis yang ditentukan oleh persamaan umum (atau implisit) berikut:
![]()
Untuk beralih dari persamaan umum ke persamaan segmental, pertama-tama kita harus mengisolasi suku bebas dari persamaan tersebut:
![]()
![]()
Kedua, kita membagi seluruh persamaan dengan koefisien di sisi kanan persamaan:
![]()
![]()
Ekspresi di atas setara dengan berikut ini:
![]()
Sehingga persamaan garis kanonik, segmental, atau simetris adalah:
![]()
Latihan 4
Tentukan persamaan kanonik atau segmental yang vektor arahnya
![]()
dan melewati titik tersebut
![]()
Pertama-tama kita dengan mudah mencari persamaan kontinu garis dari vektor arahnya dan titik yang termasuk dalam garis tersebut:
![]()
![]()
![]()
Sekarang mari kita hitung persamaan umum garis dengan mengalikan pecahan secara melintang dan mengelompokkan suku-suku yang dihasilkan:
![]()
![]()
![]()
![]()
Oleh karena itu, cukuplah mengubah persamaan umum garis menjadi persamaan kanonik. Untuk melakukan ini, pertama-tama kita hapus suku bebas dari persamaan:
![]()
Selanjutnya, kita membagi seluruh persamaan dengan koefisien di ruas kanan persamaan:
![]()
![]()
Ekspresi di atas setara dengan berikut ini:
![]()
Negatif dibagi negatif sama dengan positif:
![]()
Pecahan tidak dapat disederhanakan lebih lanjut, oleh karena itu persamaan garis kanonik, segmental, atau simetris adalah:
![]()