Persamaan parametrik bidang

Di halaman ini Anda akan menemukan apa itu persamaan parametrik suatu denah dan cara menghitungnya (rumus). Selain itu, Anda akan dapat melihat contoh dan latihan dengan latihan yang diselesaikan langkah demi langkah.

Apa persamaan parametrik suatu bidang?

Dalam geometri analitik, persamaan parametrik suatu bidang adalah persamaan yang memungkinkan bidang apa pun dinyatakan secara matematis. Untuk mencari persamaan parametrik suatu bidang, kita hanya memerlukan sebuah titik dan dua vektor bebas linier yang dimiliki bidang tersebut.

Perumusan persamaan parametrik denah

Perhatikan sebuah titik dan dua vektor arah pada sebuah bidang:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

Rumus persamaan parametrik suatu bidang adalah:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Emas

$\lambda$

Dan

$\mu$

adalah dua skalar, yaitu dua bilangan real.

Penting agar kedua vektor arah persamaan bidang tersebut bebas linier, yaitu mempunyai arah yang berbeda (tidak paralel). Jika tidak, persamaan di atas tidak mewakili rencana.

Di sisi lain, perlu diingat bahwa selain persamaan parametrik, ada cara lain untuk menyatakan bidang dalam ruang secara analitis (dalam R3), seperti persamaan bidang umum . Di tautan ini Anda akan menemukan rumusnya, cara menghitungnya dari persamaan parametrik denah, contoh, dan latihan yang diselesaikan.

Contoh cara mencari persamaan parametrik suatu bidang

Setelah kita melihat persamaan parametrik bidang, mari kita lihat cara menghitungnya menggunakan contoh:

Temukan persamaan parametrik bidang yang melalui titik tersebut
$P(1,3,2)$

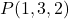
dan berisi vektor

$\vv{\text{u}}=(2,0,-1)$

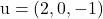
Dan

$\vv{\text{v}}=(4,2,3)$

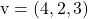
Untuk menentukan persamaan parametrik denah tersebut, cukup terapkan rumusnya:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Dan sekarang kita substitusikan titik dan masing-masing vektor arah ke dalam persamaan:

$\displaystyle \begin{cases}x=1 + \lambda \cdot 2 + \mu \cdot 4 \\[1.7ex] y=3+ \lambda \cdot 0 + \mu \cdot 2\\[1.7ex] z=2 + \lambda\cdot (-1)+ \mu \cdot 3\end{cases}$

$\displaystyle \begin{cases}\bm{x=1 + 2\lambda + 4\mu } \\[1.7ex] \bm{y=3 + 2\mu}\\[1.7ex] \bm{z=2 -\lambda+ 3\mu} \end{cases}$

Bagaimana berpindah dari persamaan vektor bidang ke persamaan parametrik

Cara lain untuk menentukan persamaan parametrik suatu bidang adalah dari persamaan vektor suatu bidang. Di bawah ini Anda dapat melihat demonya.

Biarkan persamaan vektor bidang apa pun menjadi:

$(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)$

Kami mengoperasikan dan pertama-tama melakukan perkalian vektor dengan skalar:

$(x,y,z)=(P_x,P_y,P_z)+ (\lambda\text{u}_x,\lambda\text{u}_y,\lambda\text{u}_z) +(\mu\text{v}_x,\mu\text{v}_y,\mu\text{v}_z)$

Selanjutnya kita tambahkan komponen-komponennya:

$(x,y,z)=(P_x+\lambda \text{u}_x + \mu \text{v}_x,P_y+\lambda \text{u}_y + \mu \text{v}_y,P_z+\lambda \text{u}_z + \mu \text{v}_z)$

Dan terakhir, kita memperoleh persamaan parametrik bidang dengan mengasimilasi koordinat yang bersesuaian dengan setiap variabel secara terpisah:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Seperti yang Anda lihat pada dua contoh di atas, mencari persamaan parametrik sebuah bidang relatif mudah. Namun, soalnya bisa menjadi sedikit rumit, jadi di bawah ini Anda memiliki beberapa latihan yang diselesaikan dengan tingkat kesulitan berbeda sehingga Anda bisa berlatih.

Memecahkan masalah persamaan parametrik bidang

Latihan 1

Tentukan persamaan parametrik bidang yang memuat vektor

$\vv{\text{u}}=(2,1,5)$

dan melewati dua poin berikut:

$A(3,2,-1)$

Dan

$B(-2,-1,1).$

lihat solusi

Untuk mengetahui persamaan suatu bidang, diperlukan sebuah titik dan dua vektor dan dalam hal ini kita hanya mempunyai satu vektor, oleh karena itu kita harus mencari vektor pengarah bidang lainnya. Untuk melakukan ini, kita dapat menghitung vektor yang mendefinisikan dua titik pada bidang:

$\vv{AB} = B - A = (-2,-1,1) - (3,2,-1) = (-5,-3,2)$

Sekarang kita telah mengetahui dua vektor arah bidang dan sebuah titik, maka kita menggunakan rumus persamaan parametrik bidang:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Dan kita substitusikan dua vektor dan salah satu dari dua titik pada bidang tersebut ke dalam persamaan:

$\displaystyle \begin{cases}x=3 + \lambda \cdot 2+ \mu \cdot (-5) \\[1.7ex] y=2 + \lambda \cdot 1 + \mu \cdot (-3) \\[1.7ex] z=(-1) + \lambda\cdot 5 + \mu \cdot 2 \end{cases}$

$\displaystyle \begin{cases}\bm{x=3 +2 \lambda-5\mu } \\[1.7ex] \bm{y=2 + \lambda-3 \mu } \\[1.7ex] \bm{z=-1 + 5\lambda + 2\mu } \end{cases}$

Latihan 2

Temukan persamaan parametrik bidang yang memuat tiga titik berikut:

$A(4,1,0) \qquad B(2,-3,-1) \qquad C(1,5,3)$

lihat solusi

Untuk mencari persamaan parametrik bidang tersebut, kita perlu mencari dua vektor bebas linier yang terhubung dalam bidang tersebut. Dan untuk ini, kita dapat menghitung dua vektor yang ditentukan oleh 3 titik:

$\vv{AB} = B - A = (2,-3,-1) - (4,1,0) = (-2,-4,-1)$

$\vv{AC} = C - A = (1,5,3) - (4,1,0) = (-3,4,3)$

Koordinat kedua vektor yang ditemukan tidak proporsional, sehingga saling bebas linier.

Sekarang kita telah mengetahui dua vektor arah dan sebuah titik pada bidang, kita menerapkan rumus persamaan parametrik bidang:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Dan kita substitusikan dua vektor dan salah satu dari tiga titik pada bidang tersebut ke dalam persamaan:

$\displaystyle \begin{cases}x=4 + \lambda \cdot (-2)+ \mu \cdot (-3) \\[1.7ex] y=1 + \lambda \cdot (-4) + \mu \cdot 4 \\[1.7ex] z=0 + \lambda\cdot (-1) + \mu \cdot 3 \end{cases}$

$\displaystyle \begin{cases}\bm{x=4 -2 \lambda-3\mu } \\[1.7ex] \bm{y=1-4 \lambda+4 \mu } \\[1.7ex] \bm{z=-\lambda + 3\mu } \end{cases}$

Latihan 3

Hitung persamaan parametrik bidang yang ditentukan oleh persamaan vektor berikut:

$(x,y,z)=(0,-1,5)+\lambda (6,1,-2) + \mu (1,-1,3)$

lihat solusi

Untuk mengubah persamaan vektor bidang menjadi persamaan parametrik, Anda harus mengoperasikan koordinatnya lalu menyelesaikan setiap variabel secara terpisah:

$(x,y,z)=(0,-1,5)+\lambda (6,1,-2) + \mu (1,-1,3)$

$(x,y,z)=(0,-1,5)+(6\lambda,\lambda,-2\lambda) + (\mu,-\mu,3\mu)$

$(x,y,z)=(6\lambda+\mu,-1+\lambda-\mu,5-2\lambda+3\mu)$

$\displaystyle \begin{cases}\bm{x=6\lambda+\mu } \\[1.7ex] \bm{y=-1+\lambda-\mu} \\[1.7ex] \bm{z=5-2\lambda+3\mu } \end{cases}$

Latihan 4

Temukan persamaan parametrik bidang yang memuat garis

$r$

dan sejajar dengan kanan

$s.$

menjadi garis:

$\displaystyle r: \ \begin{cases} x=1+t \\[1.7ex] y=2-3t\\[1.7ex] z=4+2t \end{cases} \qquad \qquad s: \ \frac{x-4}{2} = \frac{y+3}{2}= \frac{z-2}{-3}$

lihat solusi

Untuk mencari persamaan parametrik bidang, kita perlu mengetahui dua vektor arah dan sebuah titik pada bidang tersebut. Instruksi memberitahu kita bahwa itu berisi garis

$r$

Oleh karena itu, kita dapat mengambil vektor arah dan sebuah titik pada garis ini untuk mendefinisikan bidang tersebut. Lebih lanjut pernyataan tersebut menyatakan bahwa bidang tersebut sejajar dengan garis

$s,$

jadi kita juga bisa menggunakan vektor arah garis ini untuk persamaan bidangnya.

hak

$r$

dinyatakan dalam bentuk persamaan parametrik, sehingga komponen vektor arahnya adalah koefisien suku parameter

$t:$

$\vv{r} =(1,-3,2)$

Dan koordinat Cartesian suatu titik pada garis yang sama adalah suku-suku bebas dari persamaan parametrik:

$P(1,2,4)$

Sebaliknya garis lurus

$s$

berbentuk persamaan kontinu sehingga komponen vektor arahnya adalah penyebut pecahan:

$\vv{s} =(2,2,-3)$

Oleh karena itu, persamaan parametrik dari denah tersebut adalah:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

$\displaystyle \begin{cases}x=1 + \lambda \cdot 1+ \mu \cdot 2 \\[1.7ex] y=2 + \lambda \cdot (-3) + \mu \cdot 2 \\[1.7ex] z=4 + \lambda\cdot 2 + \mu \cdot (-3) \end{cases}$

$\displaystyle \begin{cases}\bm{x=1 + \lambda+2\mu } \\[1.7ex] \bm{y=2-3 \lambda+2 \mu } \\[1.7ex] \bm{z=4+2\lambda -3\mu } \end{cases}$

Apa persamaan parametrik suatu bidang?

Perumusan persamaan parametrik denah

Contoh cara mencari persamaan parametrik suatu bidang

Bagaimana berpindah dari persamaan vektor bidang ke persamaan parametrik

Memecahkan masalah persamaan parametrik bidang

Latihan 1

Latihan 2

Latihan 3

Latihan 4

Tinggalkan Komentar Batalkan Balasan