Persamaan kuadrat atau persamaan kuadrat adalah persamaan derajat 2 yang pangkat terbesar salah satu sukunya sama dengan 2. Artinya, persamaan tersebut dapat mempunyai hingga dua penyelesaian yang berbeda, meskipun persamaan tersebut juga dapat mempunyai penyelesaian unik atau tidak sama sekali.
Untuk menghitung solusi atau akar persamaan kuadrat, kita dapat mengikuti dua prosedur berbeda: dengan menggunakan rumus kuadrat atau dengan memfaktorkan persamaan . Pada artikel ini kami akan membahas kedua metode tersebut dan memberi Anda beberapa latihan praktis. Meskipun sebelumnya kami akan memperjelas beberapa konsep agar penjelasan keseluruhan dapat dipahami dengan baik dan Anda mendapatkan hasil maksimal dari membaca.
Jenis Persamaan Kuadrat
Kategorisasi utama antara persamaan kuadrat didasarkan pada struktur ekspresi itu sendiri. Jadi, struktur standar atau biasa dari ekspresi ini adalah sebagai berikut: ax² + bx + c . Bentuk umum ini ekuivalen dengan persamaan lengkap, namun bila terdapat suku nol atau nol, maka strukturnya dapat berubah-ubah, disitulah muncul persamaan tidak lengkap. Selanjutnya akan kami jelaskan ciri-ciri semua tipe lebih detail.
Lengkapi persamaan kuadrat
Seperti yang telah kami katakan, kita memiliki persamaan kuadrat lengkap , yang semua koefisien a, b, dan c bukan nol. Oleh karena itu, persamaan tersebut mengikuti struktur ax² + bx + c hingga huruf besarnya, karena persamaan tersebut memiliki semua suku: suku kuadrat, suku linier, dan suku bebas. Contoh tipe ini adalah persamaan berikut: x² + 2x + 1 = 0.
Persamaan kuadrat tidak lengkap
Sedangkan untuk persamaan tidak lengkap, kita dapat membedakannya berdasarkan koefisien mana yang sama dengan nol. Ingatlah bahwa jika penjelasan ini tidak menyelesaikan keraguan Anda, tepat di bawah ini adalah gambar di mana Anda dapat menemukan semua kasus yang dijelaskan langkah demi langkah.
- Persamaan tidak lengkap (b = 0): dalam situasi pertama ini kita menemukan ekspresi yang mengikuti struktur berikut: ax² + c = 0. Dengan demikian, kita memperoleh dua hasil: negatif dan positif dari akar pecahan c/a .
- Persamaan tidak lengkap (c = 0): jika kita mempunyai bentuk ax² + bx = 0 kita harus memfaktorkan persamaan tersebut agar mendapat ekspresi x (ax + b) = 0. Oleh karena itu, kita mempunyai dua penyelesaian: x = 0 dan x = – b/a.
- Persamaan tidak lengkap (b = c = 0): dalam hal ini kita mempunyai persamaan ax² = 0 dan kita hanya mempunyai satu kemungkinan solusi, yaitu x = 0.
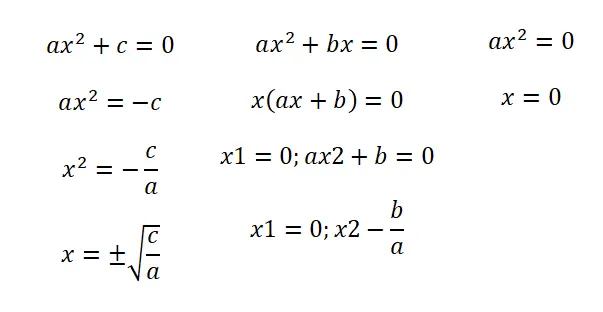
Perlu disebutkan bahwa prosedur yang kami ajarkan memungkinkan Anda menyelesaikan persamaan yang tidak lengkap dengan lebih cepat. Namun, dalam semua kasus, Anda dapat menggunakan rumus kuadrat yang akan kami ajarkan di bawah ini, Anda hanya perlu menulis nol pada koefisien yang tidak ada.
Rumus persamaan kuadrat
Untuk menyelesaikan persamaan kuadrat (ax² + bx + c = 0), kita perlu menerapkan rumus umum atau rumus kuadrat dan kemudian kita perlu mengganti nilai numerik yang sesuai dengan setiap huruf dalam ekspresi matematika.
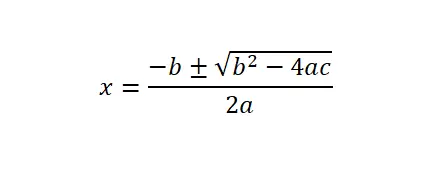
Penting juga untuk dijelaskan bahwa diskriminan (Δ) adalah ekspresi b² – 4ac, yang terletak di bawah akar kuadrat. Dari konsep matematika ini kita dapat mengetahui berapa banyak solusi yang dimiliki persamaan kuadrat tersebut. Pada dasarnya ada tiga pilihan: diskriminan negatif (tidak ada solusi nyata), diskriminan nol (hanya ada satu solusi), atau diskriminan positif (ada dua solusi).
Contoh Penyelesaian Persamaan Kuadrat Lengkap
Coba selesaikan persamaan kuadrat berikut: 2x²+4x-6=0 dan periksa hasilnya dengan persamaan di bawah ini. Kami menyarankan Anda mengikuti prosedur berikut: menganalisis jenis persamaan (mengidentifikasi suku nol), menghitung diskriminan untuk mengetahui jumlah solusi yang ada, dan terakhir, menyelesaikan persamaan yang diusulkan dengan rumus.
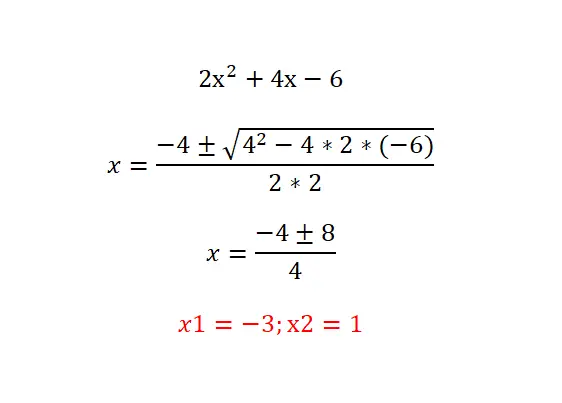
Persamaan kuadrat faktorial
Metode kedua yang kita miliki untuk menyelesaikan persamaan kuadrat adalah faktorisasi . Jadi, untuk memfaktorkan suatu polinomial (dalam kasus kita adalah polinomial kuadrat), kita dapat menggunakan metode yang berbeda. Meskipun secara umum, persamaan gaya ini biasanya dapat difaktorkan dengan suku yang sama. Dan jika tidak, Anda dapat mencoba menerapkan Notable Identities , tetapi biasanya Anda tidak perlu mengetahui metode lain apa pun dalam situasi ini.
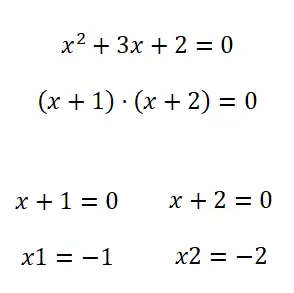
Latihan persamaan kuadrat dengan solusi
Di bawah ini Anda akan menemukan serangkaian latihan persamaan kuadrat lengkap dan tidak lengkap . Dengan cara ini Anda akan meninjau semua teori yang dijelaskan sepanjang artikel ini dan akan lebih jelas bagi Anda bagaimana menerapkannya dalam latihan. Kami menyarankan Anda mencoba menyelesaikannya sendiri dan hanya melihat solusinya ketika Anda telah menyelesaikannya atau ketika Anda mengalami kebuntuan. Meskipun demikian, Anda dapat mulai menyelesaikan latihannya sekarang.
Latihan 1
Selesaikan persamaan kuadrat berikut:
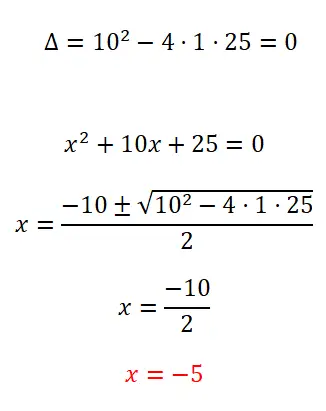
- Kita mulai dengan menghitung diskriminan, untuk mengetahui banyaknya solusi yang mungkin.
- Karena ini adalah persamaan kuadrat lengkap, kami menerapkan rumus kuadrat dan menyelesaikan perhitungannya.
- Kami memperoleh nilai x yang tidak diketahui.
Latihan 2
Selesaikan persamaan kuadrat berikut:
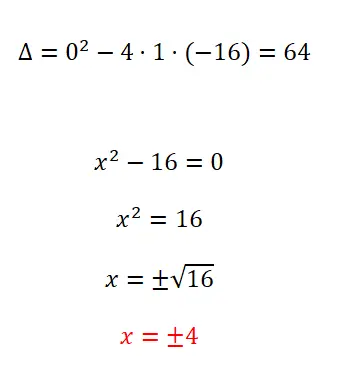
- Kita mulai dengan menghitung diskriminannya.
- Karena kita mempunyai persamaan kuadrat tidak lengkap yang b = 0, kita menerapkan standar untuk persamaan jenis ini.
- Kita selesaikan perhitungannya untuk mendapatkan hasilnya, dan kita tidak boleh melupakan tanda ±.
Latihan 3
Selesaikan persamaan kuadrat tak berurutan berikut:
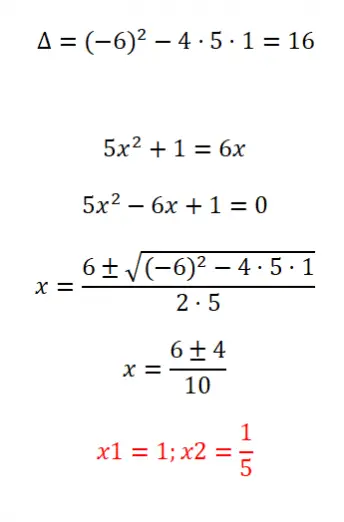
- Kita mulai dengan menghitung diskriminan persamaan tersebut.
- Sebelum kita dapat menerapkan rumusnya, kita perlu mengurutkan persamaannya berdasarkan struktur ax² + bx + c = 0.
- Kemudian kita terapkan rumus umum.
- Dan akhirnya kita mendapatkan hasilnya.
Latihan 4
Selesaikan persamaan kuadrat berikut dengan memfaktorkan:
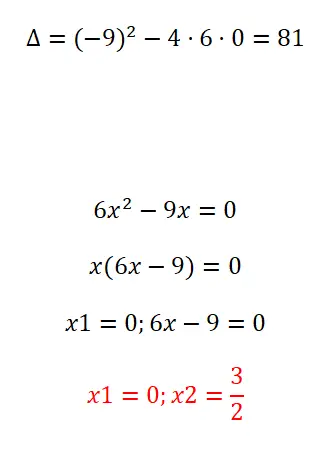
- Pertama-tama kita menghitung diskriminannya.
- Selanjutnya, kita mengekstrak faktor persekutuan dari x.
- Jadi solusi pertama adalah x = 0.
- Dan yang kedua adalah x = 3/2.
Latihan 5
Selesaikan persamaan kuadrat lengkap yang kami tunjukkan di bawah ini:
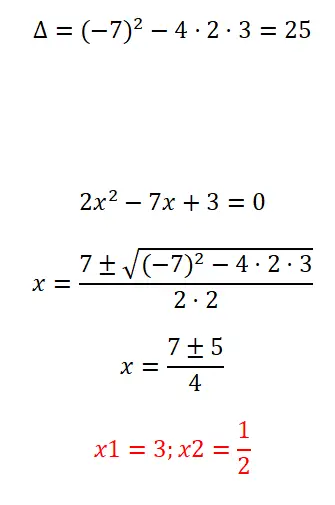
- Seperti biasa, kami menghitung diskriminan untuk mengetahui berapa banyak solusi yang dimiliki persamaan tersebut.
- Selanjutnya kita terapkan rumus kuadrat, karena merupakan persamaan lengkap.
- Terakhir, kami nyatakan hasil persamaannya.
Latihan 6
Selesaikan persamaan kuadrat dengan pecahan yang kami tawarkan:
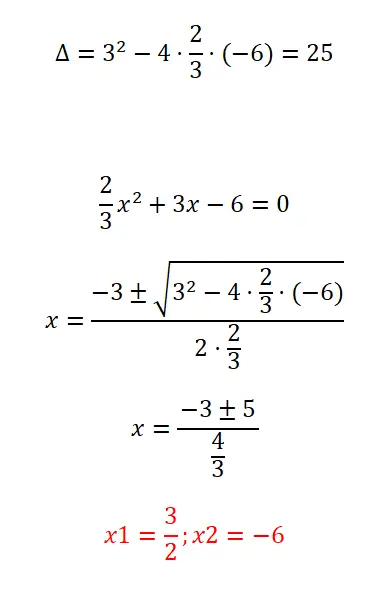
- Kita mulai dengan menghitung diskriminan dari ekspresi tersebut.
- Selanjutnya kita terapkan rumus kuadrat, dengan memperhatikan bahwa koefisien “a” dibentuk oleh pecahan.
- Kami menyelesaikan perhitungannya.
- Dan kita sudah mempunyai dua akar persamaannya.
Latihan 7
Selesaikan persamaan kuadrat berikut:
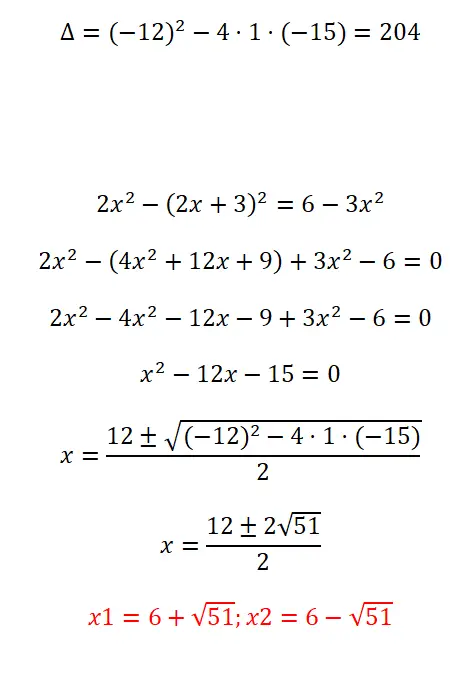
- Kita mulai dengan menghitung diskriminannya.
- Sebelum menerapkan rumus ini, kita perlu menyederhanakan persamaannya dan memberinya bentuk ax² + b + c = 0.
- Kami mengganti semua koefisien ke dalam rumus dan menyelesaikan perhitungannya.
- Akhirnya kita mendapatkan hasilnya.
Latihan 8
Bukti penyelesaian persamaan kuadrat berikut:
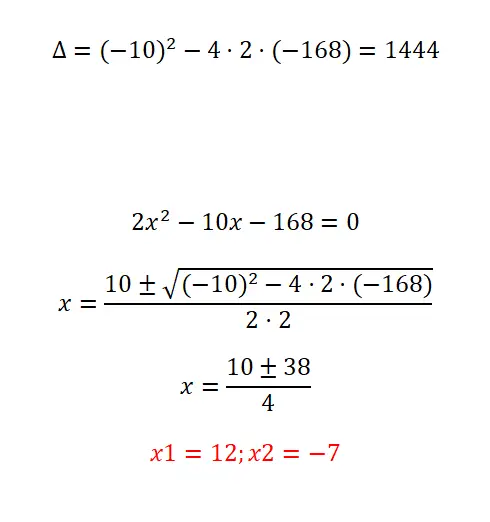
- Kita mulai dengan menghitung diskriminannya.
- Seperti yang Anda lihat, ini adalah persamaan kuadrat sederhana, meskipun koefisiennya cukup besar. Oleh karena itu, kita perlu menerapkan rumus tersebut dan berhati-hati saat melakukan pengoperasiannya.
- Pada akhirnya kami mendapatkan kedua solusi yang mungkin.