Persamaan derajat satu atau persamaan linier merupakan dasar dari aljabar , karena jika Anda tidak memahaminya maka akan sangat sulit bagi Anda untuk memahami persamaan yang lebih kompleks. Jadi, kekhasan persamaan jenis ini adalah bahwa bagian literal dari monomial tidak dapat memiliki eksponen. Oleh karena itu, dalam persamaan linier kita hanya akan menemukan monomial tanpa bagian literal dan monomial dengan bagian literal tanpa eksponen, seperti: 3 + x = -5 – 3x .
Perhatikan juga bahwa persamaan ini biasanya memiliki solusi unik, meskipun mungkin juga tidak. Untuk mengetahui kasus mana yang ada di hadapan kita, kita harus menyelesaikan persamaan tersebut dan pada akhirnya menganalisis hasilnya . Jadi, jika kita memperoleh persamaan mustahil seperti 2 = 0, maka persamaan tersebut tidak memiliki solusi. Sebaliknya jika kita memperoleh persamaan yang selalu benar, maka penyelesaiannya ekuivalen dengan semua bilangan real. Dan terakhir, jika pada akhirnya kita memperoleh persamaan X dan nilai numerik, dalam hal ini kita akan mendapatkan hasil yang unik.
Tata cara penyelesaian persamaan linear
Menyelesaikan suatu persamaan sama dengan menghitung nilai suatu variabel yang diwakili oleh huruf (x, y, a, b…). Jadi, untuk menemukan nilai ini kita perlu mengikuti langkah-langkah berikut:
- Menyelesaikan tanda kurung dan pecahan: Untuk memulai, kita hilangkan semua tanda kurung dan penyebut, agar mendapatkan persamaan yang lebih mudah dipahami. Karena kita bisa langsung mengapresiasi istilah mana yang disertai dengan hal yang tidak diketahui dan mana yang tidak, bacaan ini memudahkan kita untuk melanjutkan penyelesaian ekspresi tersebut.
- Mari kita sederhanakan ungkapannya: kita mengelompokkan suku-suku yang serupa (suku-suku independen di satu sisi, dan suku-suku dengan x di sisi lain). Jadi, di satu sisi kita akan meninggalkan angka-angka yang tidak diketahui dan kita akan meneruskan angka-angka lainnya ke sisi yang berlawanan. Tapi ingat, untuk mengubah sisinya, kita harus mengubah tandanya.
- Operasikan di setiap sisi: Kami melakukan semua operasi dalam urutan berikut: pangkat/akar, perkalian/pembagian, dan penjumlahan/pengurangan. Kita melakukan hal ini sampai kita mendapatkan satu suku pada masing-masing ruas, sehingga kita mendapatkan persamaan dengan struktur yang sama seperti ini: 4x = 8.
- Pisahkan variabelnya: terakhir, cukup berikan nilai yang menyertai huruf tersebut dengan membagi di sisi yang lain dan dengan demikian kita akan menemukan nilai akhirnya. Pada akhir langkah ini kita akan menyelesaikan permasalahan yang tidak diketahui dan kita akan mengetahui jenis hasil yang tersisa: solusi unik, solusi tidak valid, atau solusi yang memenuhi semua bilangan bulat.
Contoh Persamaan Derajat Pertama
Di bawah ini Anda akan menemukan persamaan derajat pertama yang terselesaikan , yang disusun ke dalam kategori berbeda sesuai dengan kompleksitas strukturnya. Jadi, dengan mengetahui prosedur teoritis untuk menyelesaikan persamaan linear dan jenis-jenis yang ada, Anda sudah memiliki pengetahuan yang diperlukan untuk dapat menyelesaikannya dengan mudah dan kita akan mulai dengan latihan. Karena itu, mari kita mulai dengan penjelasan teoretisnya:
Persamaan Dasar Derajat Pertama
Persamaan linier jenis pertama ini hanya terdiri dari operasi aritmatika dasar (penjumlahan, pengurangan, perkalian, dan pembagian). Berikut adalah dua contoh yang berhasil, yang pertama sedikit lebih mendasar dan yang kedua sedikit lebih rumit dalam hal perhitungan:
-6x + 4 – 1 = 6x -3
-6x + 3 = 6x – 3
-6x – 6x = -3 – 3
-12x = -6
x = 1 / 2
-24x – 3 + 4x = -4x – 27
-20x – 3 = -4x – 27
-20x + 4x = -27 + 3
-16x = -24
x = 3/2
Persamaan derajat pertama dengan tanda kurung
Kedua, kita memiliki persamaan linear dalam tanda kurung. Pemecahannya sedikit lebih rumit daripada yang sebelumnya, meskipun satu-satunya kesulitannya terletak pada perhitungannya, karena sifat-sifat tanda kurung harus diperhatikan. Untuk membuatnya lebih jelas, kami tunjukkan dua contoh yang berhasil:
2(x + 3) – 4x = -4
2x + 6 – 4x = -4
-2x = -10
x = 5
-2 + 3 (4x + 5) = -1 (x + 2) + 2 (-3x + 2)
-2 + 12x + 15 = -x – 2 – 6x + 4
13 + 12x = -7x + 2
12x + 7x = -13 + 2
19x = -11
x = -11/19
Persamaan derajat pertama dengan pangkat dan akar
Level ketiga cukup sederhana karena hanya menambah kekuatan dan akar. Satu-satunya kesulitan yang mungkin Anda temui dengan persamaan ini adalah ketika eksponen atau akar mempengaruhi tanda kurung bilangan bulat (seperti contoh kedua yang akan kami tunjukkan), namun segala sesuatunya tetap sama. Di bawah ini adalah dua contoh.
3² + √25 – 2x = 2³x + 4
9 + 5 – 2x = 8x + 4
14 – 2x = 8x + 4
-2x – 8x = -14 + 4
-10x = -10
x = 1
4x + (2 – 1 +5)² = 3x – √16
4x + 6² = 3x – 4
4x – 3x = -4 -36
x = -40
Persamaan derajat pertama dengan pecahan
Kategori persamaan linier terakhir yang dapat kita temukan adalah persamaan ini, yang terdiri dari semua elemen yang telah kita komentari sebelumnya dan juga berdasarkan pecahan. Level ini adalah yang paling kompleks dan ada beberapa metode untuk menyelesaikannya. Cara pertama dan paling sederhana adalah mengalikan penyebutnya dengan sisi kebalikan dari persamaan tersebut, meskipun kita hanya dapat menggunakannya jika kita memiliki dua pecahan. Sebaliknya, jika kita mempunyai lebih dari dua pecahan dalam persamaan, kita harus mencari penyebut yang sama dan mengalikan semua pecahan dengan membagi nilai tersebut dengan penyebut pecahan yang sama. Di bawah ini adalah contoh masing-masing jenis:
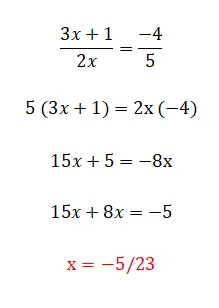
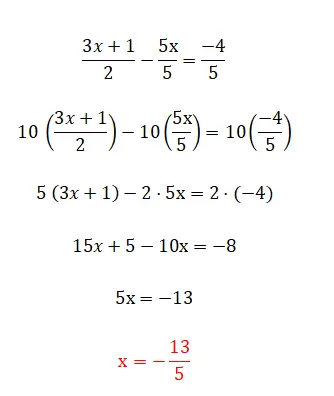
Latihan persamaan derajat pertama
Sekarang kami menawarkan beberapa latihan persamaan linear. Persamaan tersebut disusun berdasarkan tingkat kesulitan yang semakin meningkat, dengan persamaan pertama lebih mudah daripada persamaan terakhir. Oleh karena itu, kami menyarankan Anda memulai dari awal dan melihat seberapa jauh Anda dapat melangkah. Jadi, coba selesaikan persamaan berikut lalu bandingkan hasil Anda dengan solusi yang kami berikan.
Latihan pertama
Latihan pertama adalah persamaan linier yang sangat sederhana, karena hanya terdiri dari penjumlahan dan pengurangan, dan juga hanya memiliki empat suku antara kedua sisi persamaan:
2x – 3 = 4x + 5
2x – 4x = 5 + 3
-2x = 8
x = 8 / (-2)
x = -4
- Kami mengelompokkan istilah serupa menjadi satu.
- Kami menyederhanakan kedua sisi.
- Kami menghapus yang tidak diketahui dan menghitung nilainya.
latihan kedua
Dalam kasus ini, kita menemukan persamaan yang dibentuk oleh tanda kurung, yang mana prioritas utama kita adalah menghilangkan persamaan tersebut, sehingga kita kemudian dapat mengelompokkan suku-suku serupa:
-4(x + 2) + 5x = 6 + 5x
-4x – 8 + 5x = 6 + 5x
-4x + 5x – 5x = 6 + 8
-4x = 14
x = 14 / (-4) = -7 / 2
- Kami memecahkan tanda kurung.
- Kita pindahkan tanda x ke kiri dan suku bebasnya ke kanan.
- Kami mengklarifikasi hal yang tidak diketahui.
Kami menyederhanakan hasilnya.
latihan ketiga
Selanjutnya, Anda harus menyelesaikan persamaan kuadrat lainnya dengan tanda kurung, meskipun persamaan ini sedikit lebih sulit. Hal ini karena memiliki tanda kurung bersarang (tanda kurung di dalam tanda kurung lainnya). Oleh karena itu, Anda harus mengikuti urutan penyelesaian dengan benar: pertama orang dalam, kemudian orang luar.
3x + 2 (x – (4x – 5)) = 1 – (3 (2x + 7) – 2)
3x + 2 (x – 4x + 5) = 1 – (6x + 21 – 2)
3x + 2x – 8x + 10 = 1 – 6x – 21 + 2
-3x + 10 = -6x – 18
3x = -28
x = -28/3
- Kita mulai dengan menyelesaikan tanda kurung bagian dalam.
- Selanjutnya, kita menyelesaikan tanda kurung luar.
- Kami menyederhanakan kedua sisi persamaan dan mengumpulkan suku-suku serupa.
- Kami mengisolasi x dan menghitung nilainya.
latihan keempat
Dalam latihan ini kita mulai melihat pecahan, yang mungkin merupakan elemen persamaan linear yang paling rumit. Meski begitu jangan khawatir karena jika Anda sudah membaca teorinya Anda pasti tahu betul bagaimana melakukannya:
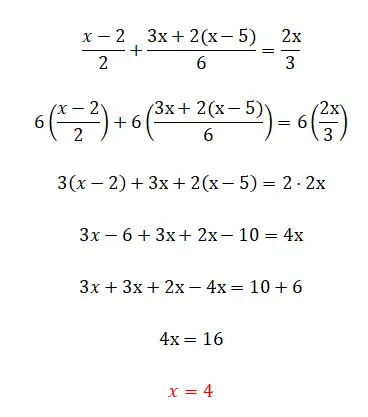
Latihan kelima
Dalam latihan kelima ini, kita melihat pecahan dalam tanda kurung, yang berarti hierarki penyelesaiannya menjadi sedikit rumit. Perlu disebutkan bahwa contoh ini dapat diselesaikan dengan menggunakan dua metode: menggunakan metode kelipatan persekutuan terkecil atau dengan mengoperasikan pecahan secara langsung. Di bawah ini Anda dapat melihat dua prosedur lengkapnya:
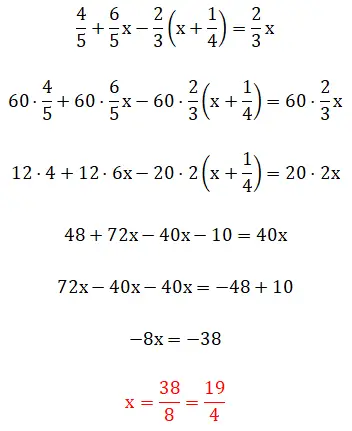
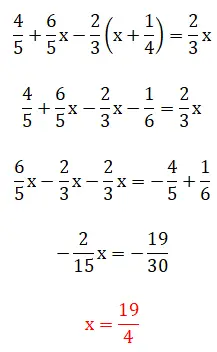
latihan keenam
Selanjutnya, kita melangkah lebih jauh dengan topik pecahan dan tanda kurung, karena kita memiliki tanda kurung bertumpuk. Latihan ini tidak membawa lebih banyak kerumitan dibandingkan latihan sebelumnya, hanya saja sedikit lebih sulit dalam hal perhitungan dan hanya itu.
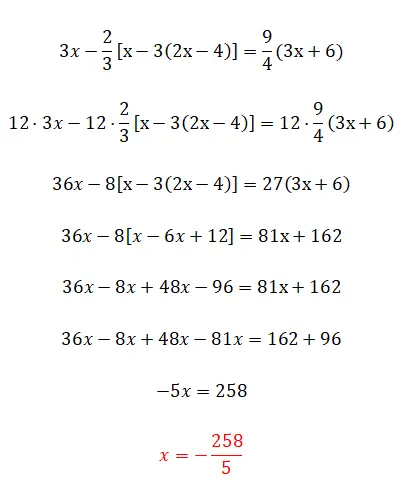
- Kami mengalikan semua suku dengan lcmp penyebutnya.
- Kami menyederhanakan ekspresi dengan menghilangkan tanda kurung: pertama yang di dalam, lalu yang di luar.
- Kami mengelompokkan istilah serupa di setiap sisi.
- Kami menyelesaikan operasi di masing-masing pihak.
- Dan kami menghitung nilai yang tidak diketahui.
latihan ketujuh
Latihan berikut mungkin tampak sangat mudah, tetapi kami menyarankan Anda tetap mencoba menyelesaikannya, karena ini pasti akan memberi Anda hasil yang agak tidak biasa. Setelah mencobanya, simak solusi dan penjelasan latihannya di bawah ini.
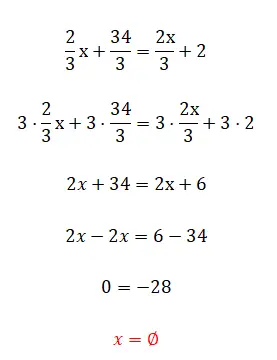
- Kita mengalikan semua pecahan dengan lcm penyebutnya.
- Kami menyederhanakan ekspresi yang diperoleh.
- Dan akhirnya kita melihat bahwa hal ini memberi kita persamaan yang salah, karena kita telah menghilangkan hal-hal yang tidak diketahui.
Seperti yang mungkin Anda ketahui, ini adalah persamaan palsu atau persamaan tanpa hasil, karena tidak ada nilai yang melengkapi persamaan tersebut dengan benar. Ini adalah salah satu kasus yang kami sebutkan di pendahuluan.
latihan kedelapan
Terakhir, kami menawarkan kepada Anda latihan ini yang cukup rumit karena memiliki semua komplikasi yang telah kita lihat di seluruh artikel ini, meskipun juga memiliki sedikit trik. Beri komentar bahwa jika Anda mampu menyelesaikan persamaan derajat pertama ini, maka Anda telah memahami keseluruhan teori dengan sempurna. Dan jika belum, jangan khawatir, karena latihan ini cukup rumit.
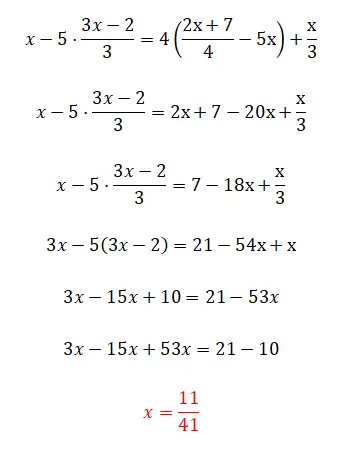
- Kita mulai dengan menghilangkan empat angka di sisi kanan persamaan.
- Lalu kita gabung dengan tanda x di sisi kanan.
- Kita mengalikan semua suku dengan tiga untuk menghilangkan penyebutnya.
- Kami menghapus tanda kurung.
- Kami menggabungkan istilah serupa.
- Kami menghitung nilai yang tidak diketahui.
Lebih banyak latihan persamaan linier
Sekarang setelah Anda cukup berlatih, Anda seharusnya bisa menyelesaikan persamaan linear kompleks . Meskipun jika Anda ingin terus berlatih, kami menyarankan Anda mencoba menyelesaikan lembar kerja ini. Namun jika Anda merasa sudah cukup membahasnya, kami juga dapat menawarkan artikel yang dapat membantu Anda memahami hierarki operasi . Dengan cara ini Anda akan selalu mengetahui perhitungan mana yang harus diselesaikan terlebih dahulu dan Anda tidak akan pernah membuat kesalahan .