Di halaman ini Anda akan menemukan rumus untuk semua persamaan dalam denah dan cara menghitungnya. Anda juga akan menemukan cara mencari persamaan bidang apa pun dengan vektor normalnya. Selain itu, Anda akan dapat melihat contoh dan latihan dengan latihan persamaan denah yang diselesaikan.
Apa persamaan bidangnya?
Dalam geometri analitik, persamaan bidang adalah persamaan yang memungkinkan bidang apa pun dinyatakan secara matematis. Jadi, untuk mencari persamaan suatu bidang, Anda hanya memerlukan sebuah titik dan dua vektor bebas linier yang dimiliki bidang tersebut.
Sebelum melanjutkan ke penjelasan persamaan bidang, ada baiknya anda memahami apa itu bidang (geometri) , karena jika tidak maka akan ada hal-hal yang tidak anda pahami. Jika Anda belum sepenuhnya paham, Anda dapat memeriksanya di tautan ini, tempat kami memusatkan semua yang perlu Anda ketahui tentang rencana tersebut.
Apa persamaan rencana tersebut?
Seperti yang kita lihat pada definisi persamaan bidang, setiap titik pada bidang datar dapat dinyatakan sebagai kombinasi linier dari 1 titik dan 2 vektor.

Namun, syarat yang diperlukan agar persamaan tersebut dapat berkorespondensi dengan suatu bidang adalah bahwa kedua vektor pada bidang tersebut mempunyai independensi linier, yaitu kedua vektor tersebut tidak boleh sejajar satu sama lain.
Jadi, semua jenis persamaan bidang adalah: persamaan vektor , persamaan parametrik , persamaan implisit (atau umum) , dan persamaan bidang kanonik (atau segmental) .
Selanjutnya kita akan melihat secara detail penjelasan dan rumus semua persamaan denahnya.
Persamaan vektor bidang
Perhatikan sebuah titik dan dua vektor arah pada sebuah bidang:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
Rumus persamaan vektor suatu bidang adalah:
![]()
Atau setara:
![]()
Emas
![]()
Dan
![]()
adalah dua skalar, yaitu dua bilangan real.
Persamaan parametrik bidang
Persamaan parametrik suatu bidang dapat ditentukan dari persamaan vektornya. Di bawah ini Anda dapat melihat demonya.
Biarkan persamaan vektor bidang apa pun menjadi:
![]()
Kami mengoperasikan dan pertama-tama melakukan perkalian vektor dengan skalar:
![]()
Selanjutnya kita tambahkan komponen-komponennya:
![]()
Dan terakhir, kita memperoleh persamaan parametrik denah tersebut dengan mengasimilasi koordinat yang bersesuaian dengan setiap variabel secara terpisah:
![]()
Emas:
-
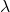
Dan
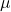
adalah dua skalar, yaitu dua bilangan real.
-
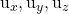
adalah komponen dari salah satu dari dua vektor pemandu denah tersebut
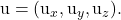
-
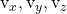
adalah komponen vektor pengarah denah lainnya
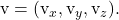
Persamaan bidang implisit atau umum
Perhatikan sebuah titik dan dua vektor arah pada sebuah bidang:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
Persamaan implisit, umum, atau Cartesian suatu bidang diperoleh dengan menyelesaikan determinan berikut dan menetapkan hasilnya sama dengan 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
Dengan demikian, persamaan implisit atau umum dari rencana yang dihasilkan adalah sebagai berikut:
![]()
Persamaan bidang jenis ini disebut juga persamaan bidang kartesius.
Persamaan bidang kanonik atau segmental
Rumus persamaan kanonik atau segmental suatu bidang adalah sebagai berikut:
![]()
Emas:
-

adalah titik potong antara bidang dan sumbu X.
-

adalah titik potong antara bidang dan sumbu Y.
-

Di sinilah bidang memotong sumbu Z.
Persamaan kanonik (atau persamaan segmental) bidang juga dapat diperoleh dari persamaan umumnya:
![]()
Pertama, kita selesaikan koefisien D dari persamaan:
![]()
Kemudian kita membagi seluruh persamaan denah dengan nilai parameter D yang diubah tandanya:
![]()
![]()
Dan, dengan menggunakan sifat-sifat pecahan, kita sampai pada ekspresi berikut:
![]()
Oleh karena itu, dari ungkapan ini kami menyimpulkan rumus yang memungkinkan suku-suku persamaan kanonik atau segmental suatu bidang dihitung secara langsung:
![]()
Oleh karena itu, untuk dapat membentuk varian persamaan denah tersebut, koefisien A, B, dan C harus berbeda dari nol, sehingga menghindari ketidakpastian pecahan.
Cara menghitung persamaan bidang dari vektor normalnya
Masalah yang sangat umum dalam persamaan bidang adalah mencari persamaan bidang tertentu jika diberi sebuah titik dan vektor normalnya (atau tegak lurus). Jadi, mari kita lihat cara kerjanya.
Namun perlu diketahui terlebih dahulu bahwa komponen X, Y, Z dari vektor tegak lurus bidang tersebut masing-masing berimpit dengan koefisien A, B, C dari persamaan implisit (atau umum) bidang tersebut.
![]()
Emas
![]()
adalah vektor ortogonal terhadap bidang
![]()
Setelah kita mengetahui hubungan sebelumnya, mari kita lihat contoh penyelesaian soal persamaan bidang jenis ini:
- Tentukan persamaan implisit atau umum bidang yang melalui titik tersebut
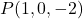
dan salah satu vektor normalnya adalah
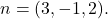
Rumus persamaan bidang implisit, umum, atau kartesius adalah:
![]()
Jadi, dari vektor normal kita dapat mencari koefisien A, B dan C karena ekuivalen dengan komponen-komponen vektor normalnya:
![]()
Sedangkan kita hanya perlu mencari parameter D. Caranya, kita substitusikan koordinat titik milik bidang tersebut ke dalam persamaan:
![]()
![]()
![]()
![]()
![]()
Jadi persamaan implisit atau umum dari rencana tersebut adalah:
![]()
Memecahkan Masalah Persamaan Bidang
Latihan 1
Tentukan persamaan vektor bidang yang memuat vektor tersebut
![]()
dan melewati dua poin berikut:
![]()
Dan
![]()
Untuk mengetahui persamaan suatu bidang, diperlukan sebuah titik dan dua vektor dan dalam hal ini kita hanya mempunyai satu vektor, oleh karena itu kita harus mencari vektor pengarah bidang lainnya. Untuk melakukan ini, kita dapat menghitung vektor yang mendefinisikan dua titik pada bidang:
![]()
Sekarang kita telah mengetahui dua vektor arah bidang dan sebuah titik, maka kita menggunakan rumus persamaan vektor bidang:
![]()
Dan kita substitusikan dua vektor dan salah satu dari dua titik pada bidang tersebut ke dalam persamaan:
![]()
Latihan 2
Temukan persamaan parametrik bidang yang memuat tiga titik berikut:
![]()
Untuk mencari persamaan parametrik bidang tersebut, kita perlu mencari dua vektor bebas linier yang terhubung dalam bidang tersebut. Dan untuk ini, kita dapat menghitung dua vektor yang ditentukan oleh 3 titik:
![]()
![]()
Koordinat kedua vektor yang ditemukan tidak proporsional, sehingga saling bebas linier.
Sekarang kita telah mengetahui dua vektor arah dan sebuah titik pada bidang, kita menerapkan rumus persamaan parametrik bidang:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5adabb85c9285653d6b638f7c48ba50_l3.png)
Dan kita substitusikan dua vektor dan salah satu dari tiga titik pada bidang tersebut ke dalam persamaan:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=4 + \lambda \cdot (-2)+ \mu \cdot (-3) \\[1.7ex] y=1 + \lambda \cdot (-4) + \mu \cdot 4 \\[1.7ex] z=0 + \lambda\cdot (-1) + \mu \cdot 3 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f57edaf8a85108cffb796470ffca8484_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}\bm{x=4 -2 \lambda-3\mu } \\[1.7ex] \bm{y=1-4 \lambda+4 \mu } \\[1.7ex] \bm{z=-\lambda + 3\mu } \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4cab5ddc074bd7df6849d71854207cf5_l3.png)
Latihan 3
Temukan persamaan implisit atau umum dari bidang yang melalui titik tersebut
![]()
dan berisi vektor
![]()
Dan
![]()
Untuk menghitung persamaan umum atau implisit bidang, perlu diselesaikan determinan yang dibentuk oleh dua vektor, ketiga variabel, dan koordinat titik berikut:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-917f1770ff2a17897e5df76998ec3519_l3.png)
Jadi, kita substitusikan vektor dan titik ke dalam rumus:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}4 & 5 & x+2 \\[1.1ex]1 & 3 & y-1 \\[1.1ex]3& 1 & z+1 \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-02e103601cd9992a8a8c087d016a08c1_l3.png)
Dan sekarang kita selesaikan determinan matriks 3×3 dengan metode pilihan Anda:
![]()
Terakhir, kami melakukan operasi dan mengelompokkan istilah serupa:
![]()
![]()
![]()
Jadi persamaan implisit atau umum dari rencana tersebut adalah:
![]()
Latihan 4
Tentukan apakah intinya
![]()
milik rencana berikut:
![]()
Agar suatu titik berada pada bidang, persamaannya harus diverifikasi. Oleh karena itu, kita perlu mensubstitusikan koordinat Cartesius titik tersebut ke dalam persamaan bidang dan memeriksa apakah persamaan tersebut terpenuhi:
![]()
![]()
![]()
![]()
![]()
Intinya tidak memperhatikan persamaan bidang tersebut, sehingga bukan bagian dari bidang tersebut.
Latihan 5
Temukan persamaan segmental bidang yang persamaan umum (atau implisitnya) adalah:
![]()
Pertama, kita hapus suku bebas dari persamaan:
![]()
Kemudian kita membagi seluruh persamaan denah dengan nilai koefisien D yang diubah tandanya:
![]()
![]()
Dan, dengan menggunakan sifat-sifat pecahan, kita sampai pada ekspresi berikut:
![]()
Jadi persamaan segmental (atau kanonik) bidang tersebut adalah:
![]()
Latihan 6
Menghitung persamaan implisit atau umum bidang dalam ruang yang melalui suatu titik
![]()
dan salah satu vektor normalnya adalah
![]()
Rumus persamaan bidang implisit, umum, atau kartesius adalah:
![]()
Nah, dari vektor normal kita dapat mencari koefisien A, B dan C, karena masing-masing sama dengan komponen vektor normalnya:
![]()
Jadi kita hanya perlu mencari parameter D. Caranya, kita substitusikan koordinat titik milik bidang tersebut ke dalam persamaan:
![]()
![]()
![]()
![]()
![]()
Kesimpulannya, persamaan implisit atau umum dari rencana tersebut adalah:
![]()
Latihan 7
Temukan persamaan parametrik bidang yang memuat garis
![]()
dan sejajar dengan kanan
![]()
menjadi garis:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=1+t \\[1.7ex] y=2-3t\\[1.7ex] z=4+2t \end{cases} \qquad \qquad s: \ \frac{x-4}{2} = \frac{y+3}{2}= \frac{z-2}{-3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-624f315685b292c4bb05e9cb4b931a97_l3.png)
Untuk mencari persamaan parametrik bidang, kita perlu mengetahui dua vektor arah dan sebuah titik pada bidang tersebut. Deklarasi tersebut memberi tahu kita bahwa deklarasi tersebut berisi garis
![]()
Oleh karena itu, kita dapat mengambil vektor arah dan sebuah titik pada garis ini untuk mendefinisikan bidang tersebut. Lebih lanjut pernyataan tersebut menyatakan bahwa bidang tersebut sejajar dengan garis
![]()
jadi kita juga bisa menggunakan vektor arah garis ini untuk persamaan bidangnya.
hak
![]()
dinyatakan dalam bentuk persamaan parametrik, sehingga komponen vektor arahnya adalah koefisien suku parameter
![]()
![]()
Dan koordinat Cartesian suatu titik pada garis yang sama adalah suku-suku bebas dari persamaan parametrik:
![]()
Sebaliknya garis lurus
![]()
berbentuk persamaan kontinu sehingga komponen vektor arahnya adalah penyebut pecahan:
![]()
Oleh karena itu, persamaan parametrik dari denah tersebut adalah:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5adabb85c9285653d6b638f7c48ba50_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=1 + \lambda \cdot 1+ \mu \cdot 2 \\[1.7ex] y=2 + \lambda \cdot (-3) + \mu \cdot 2 \\[1.7ex] z=4 + \lambda\cdot 2 + \mu \cdot (-3) \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c81f4d8e5aa907f111b3389d5137736e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}\bm{x=1 + \lambda+2\mu } \\[1.7ex] \bm{y=2-3 \lambda+2 \mu } \\[1.7ex] \bm{z=4+2\lambda -3\mu } \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fccd86ac9a3e4084e324d8e5b1071e59_l3.png)