Perkalian vektor dengan angka

Halaman ini menjelaskan cara mengalikan vektor dengan bilangan real (atau skalar) secara numerik dan grafis. Selain itu, Anda juga akan menemukan contoh dan latihan penyelesaian hasil kali vektor dengan skalar. Terakhir, sifat-sifat operasi vektor jenis ini juga dijelaskan.

Bagaimana cara mengalikan vektor dengan bilangan real?

Untuk menghitung hasil kali suatu vektor dan suatu bilangan (atau skalar) secara numerik, setiap komponen vektor harus dikalikan dengan bilangan tersebut.

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

$k\cdot \vv{\text{u}} =(k\cdot \text{u}_x \ , \ k\cdot \text{u}_y)$

Jadi, hasil perkalian suatu vektor dengan suatu bilangan akan menghasilkan vektor baru yang mempunyai ciri-ciri sebagai berikut:

Hasil perkalian suatu vektor dengan skalar menghasilkan vektor baru yang arahnya sama dengan vektor aslinya.
Selain itu, vektor baru akan mempunyai arah yang sama jika bilangannya positif.
Atau sebaliknya jika bilangannya negatif.
Besarnya vektor yang dihasilkan sama dengan besar vektor asal dikalikan skalar.

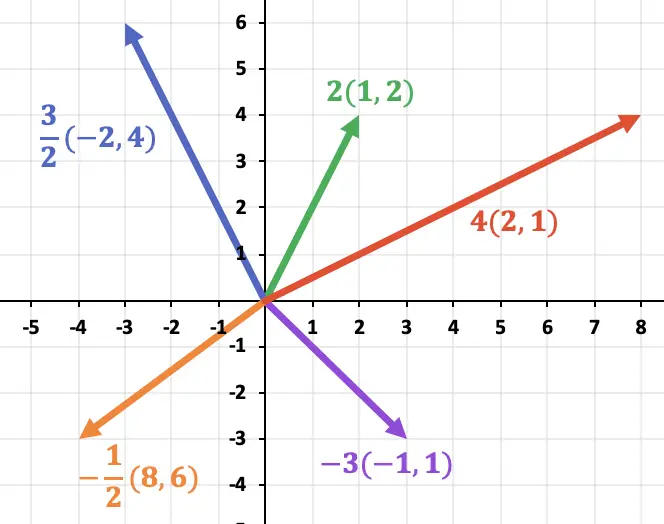
Pada grafik berikut Anda dapat melihat bagaimana arah vektor dipertahankan terlepas dari tanda skalarnya. Sebaliknya, arah vektor bergantung pada tanda bilangan yang dikalikan.

perkalian atau hasil kali suatu bilangan atau skalar dengan suatu vektor

Selanjutnya pada grafik berikut terlihat jelas bahwa besar vektor hasil kali sama dengan besar vektor asal dikalikan skalar.

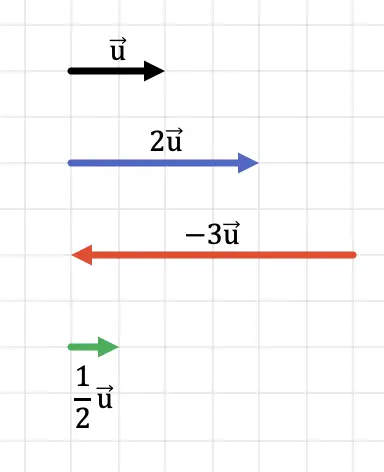
Bagaimana modul perkalian atau hasil kali suatu bilangan dengan vektor berkembang?

Jelasnya, jika kita mengalikan vektor dengan angka yang lebih besar dari 1, hasilnya adalah vektor yang panjangnya lebih besar (modulusnya lebih besar). Sebaliknya jika kita mengalikan vektor dengan bilangan yang kurang dari 1, maka hasilnya adalah vektor yang panjangnya lebih pendek (modulusnya lebih kecil).

Catatan: Jangan bingung antara hasil kali vektor dan skalar dengan hasil kali titik vektor . Meskipun memiliki nama yang mirip, keduanya merupakan dua konsep yang sangat berbeda.

Contoh perkalian vektor dengan skalar

Selanjutnya, kita akan melihat contoh numerik tentang cara menghitung hasil kali vektor dan bilangan:

Kalikan vektor berikut dengan 4:

$\vv{\text{u}} =(2,-3)$

$4\cdot \vv{\text{u}} =(4 \cdot 2 \ , \ 4 \cdot (-3)) = \bm{(8,-12)}$

Seperti yang Anda lihat, operasi vektor jenis ini tidak terlalu rumit, karena Anda tidak perlu melakukan banyak perhitungan.

Namun, ada operasi vektor yang lebih rumit, seperti penjumlahan vektor dan pengurangan vektor. Jika Anda sudah memahami cara menghitung hasil kali vektor dan skalar, kami sarankan Anda melanjutkan ke tingkat berikutnya dan melihat cara menyelesaikan penjumlahan vektor dan pengurangan vektor , karena ini adalah operasi yang lebih sulit dan, pada kenyataannya, mereka lebih banyak digunakan (mereka lebih penting).

Sifat mengalikan vektor dengan bilangan

Hasil kali suatu vektor dan suatu bilangan mempunyai sifat-sifat sebagai berikut:

Sifat asosiatif : Jika suatu vektor dikalikan dengan lebih dari satu bilangan, maka urutan perkaliannya tidak menjadi masalah.

$k \cdot (k' \cdot \vv{\text{u}}) =(k\cdot k') \cdot \vv{\text{u}}$

Sifat distributif terhadap penjumlahan dan pengurangan vektor:

$k \cdot (\vv{\text{u}}+ \vv{\text{v}})=k\cdot \vv{\text{u}} + k\cdot \vv{\text{v}}$

$k \cdot (\vv{\text{u}}- \vv{\text{v}})=k\cdot \vv{\text{u}} - k\cdot \vv{\text{v}}$

Sifat distributif terhadap penjumlahan skalar:

$(k+k') \cdot \vv{\text{u}} =k\cdot \vv{\text{u}} + k'\cdot \vv{\text{u}}$

Elemen netral : Jelas, vektor apa pun dikalikan dengan 1 menghasilkan vektor itu sendiri:

$1\cdot \vv{\text{u}} = \vv{\text{u}}$

Menyelesaikan masalah perkalian vektor dengan skalar

Latihan 1

Hitung secara analitis hasil perkalian vektor berikut dengan 3:

$\vv{a}=(-2,5)$

lihat solusi

Untuk mencari hasil kali, Anda harus mengalikan setiap koordinat vektor dengan 3:

$3\cdot \vv{a}=(3\cdot (-2), 3 \cdot 5) = \bm{(-6,15)}$

Latihan 2

Kalikan vektor berikut dengan 6 dan temukan modulnya:

$\vv{a}=(3,-4)$

lihat solusi

Pertama-tama kita mengalikan vektor dengan skalar:

$6\cdot \vv{a}=(6\cdot 3, 6 \cdot (-4)) = (18,-24)$

Saat ini ada dua cara untuk menghitung besarnya vektor yang diperoleh. Yang pertama cari besar vektor aslinya, lalu kalikan dengan 6:

$\lvert \vv{a} \rvert =\sqrt{3^2+(-4)^2} = \sqrt{25} =5$

$6\cdot \lvert \vv{a} \rvert =6\cdot 5 =\bm{30}$

Dan cara kedua adalah dengan menghitung langsung besaran vektor yang diperoleh dari perkalian:

$\lvert 6\cdot \vv{a} \rvert =\sqrt{18^2+(-24)^2} = \sqrt{900} =\bm{30}$

Sehingga dengan kedua prosedur tersebut terlihat bahwa hasilnya tidak bergantung pada metode penghitungan modulus.

Latihan 3

Dari vektor berikut:

$\vv{a}=(4,-1)$

Hitung operasi berikut secara aljabar:

$2\cdot \vv{a}$

$-3\cdot \vv{a}$

$\displaystyle \frac{1}{2} \cdot \vv{a}$

$4\cdot \vv{a}$

Selanjutnya tentukan apakah vektor-vektor yang dihasilkan mempunyai arah dan arah yang sama dengan vektor aslinya, dan urutkan dari yang terpendek ke terpanjang.

lihat solusi

Kita hitung dulu perkaliannya:

$2\cdot \vv{a}=(2\cdot 4, 2 \cdot (-1)) = (8,-2)$

$-3\cdot \vv{a}=(-3\cdot 4, -3 \cdot (-1)) = (-12,3)$

$\displaystyle \frac{1}{2}\cdot \vv{a}=\left(\frac{1}{2}\cdot 4, \frac{1}{2} \cdot (-1)\right) = \left(2,-\frac{1}{2}\right)$

$4\cdot \vv{a}=(4\cdot 4, 4 \cdot (-1)) = (16,-4)$

Oleh karena itu, vektor yang dikalikan dengan bilangan positif mempunyai arah dan arah yang sama dengan vektor aslinya. Dan vektor-vektor yang dikalikan dengan bilangan negatif mempunyai arah yang sama tetapi berlawanan arah dengan vektor aslinya.

Vektor-vektor yang searah dan searah:

$\displaystyle 2\vv{a}, \ 4\vv{a}$

Dan

$\displaystyle \frac{1}{2}\vv{a}$

Vektor yang arahnya sama tetapi maknanya berbeda:

$-3\vv{a}$

Terakhir, kita harus mengurutkan vektor-vektor menurut panjangnya, atau modulusnya. Vektor dengan panjang terpanjang (atau modul terbesar) adalah vektor yang dikalikan dengan bilangan lebih besar (dalam nilai absolut), dan vektor dengan panjang terpendek (atau modul terkecil) adalah vektor yang dikalikan dengan bilangan lebih kecil angka (dalam nilai absolut). Jadi urutan panjangnya adalah:

$\displaystyle \begin{vmatrix} \displaystyle\frac{1}{2}\vv{a}\end{vmatrix} <\lvert 2\vv{a}\rvert < \lvert -3\vv{a}\rvert < \lvert 4\vv{a}\rvert$