Perkalian suatu bilangan dengan matriks

Pada halaman ini kita akan melihat cara mengalikan suatu bilangan dengan matriks. Anda juga memiliki contoh yang akan membantu Anda memahaminya dengan sempurna dan menyelesaikan latihan sehingga Anda dapat berlatih. Anda juga akan menemukan semua properti hasil kali skalar dan matriks.

Bagaimana cara mengalikan suatu bilangan dengan matriks?

Untuk mengalikan suatu bilangan dengan matriks , kalikan setiap elemen matriks dengan bilangan tersebut.

Contoh:

Menyelesaikan masalah perkalian suatu bilangan dengan matriks

Latihan 1:

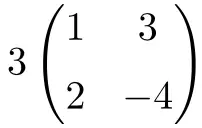
Menyelesaikan latihan perkalian suatu bilangan dengan matriks 2x2, operasi dengan matriks

lihat solusi

Ini adalah perkalian skalar dengan matriks persegi berorde 2:

$\displaystyle 3 \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -4 \end{pmatrix} = \begin{pmatrix} 3\cdot 1 & 3\cdot 3 \\[1.1ex] 3\cdot 2 & 3\cdot (-4) \end{pmatrix} = \begin{pmatrix} \bm{3} & \bm{9} \\[1.1ex] \bm{6} & \bm{-12} \end{pmatrix}$

Latihan 2:

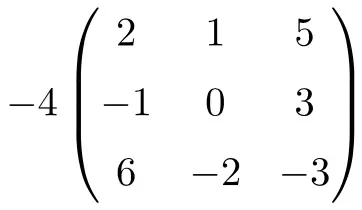
latihan diselesaikan langkah demi langkah perkalian suatu bilangan dengan matriks 3x3, operasi dengan matriks

lihat solusi

Ini adalah hasil kali suatu bilangan dengan matriks persegi berorde 3:

$\displaystyle -4 \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -1 & 0 & 3 \\[1.1ex] 6 & -2 & -3 \end{pmatrix} = \begin{pmatrix} -4 \cdot 2 & -4 \cdot 1 & -4 \cdot 5 \\[1.1ex] -4 \cdot (-1) & -4 \cdot 0 & -4 \cdot 3 \\[1.1ex] -4 \cdot 6 & -4 \cdot (-2) & -4 \cdot (-3) \end{pmatrix}= \begin{pmatrix} \bm{-8} & \bm{-4} & \bm{-20} \\[1.1ex] \bm{4} & \bm{0} & \bm {-12} \\[1.1ex] \bm{-24} & \bm{8} & \bm {12} \end{pmatrix}$

Latihan 3:

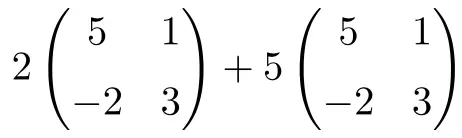
Soal latihan perkalian suatu bilangan dengan matriks 2x2, operasi gabungan matriks

lihat solusi

Ini adalah operasi yang menggabungkan hasil kali bilangan dengan matriks dan jumlah matriks berdimensi 2×2:

$\displaystyle 2 \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 3 \end{pmatrix}+5\begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 3 \end{pmatrix}$

Oleh karena itu, pertama-tama kita perlu menyelesaikan produk:

$\displaystyle \begin{pmatrix} 10 & 2 \\[1.1ex] -4 & 6 \end{pmatrix}+\begin{pmatrix} 25 & 5 \\[1.1ex] -10 & 15 \end{pmatrix}$

Dan terakhir kita menjumlahkan matriks yang dihasilkan:

$\displaystyle \begin{pmatrix} \bm{35} & \bm{7} \\[1.1ex] \bm{-14} & \bm{21} \end{pmatrix}$

Latihan 4:

Perhatikan matriks berikut:

$\displaystyle A=\begin{pmatrix} 2 & -3 & 5 \\ 1 & 4 & 0 \\ -3 & 2 & -5 \end{pmatrix} \qquad B=\begin{pmatrix} 6 & 0 & 2 \\ -3 & 4 & 1 \\ 3 & 2 & 7 \end{pmatrix}$

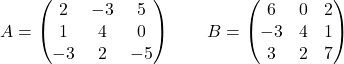
Menghitung:

$\displaystyle -2A+5I-3B$

lihat solusi

Merupakan operasi yang menggabungkan perkalian skalar dengan penjumlahan dan pengurangan matriks berdimensi 3×3. Selanjutnya matriks

$I$

adalah matriks identitas, yang terdiri dari 1 pada diagonal utama dan 0 pada elemen lainnya:

$\displaystyle -2\begin{pmatrix} 2 & -3 & 5 \\[1.1ex] 1 & 4 & 0 \\[1.1ex] -3 & 2 & -5 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} -3 \begin{pmatrix} 6 & 0 & 2 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 3 & 2 & 7 \end{pmatrix}$

Oleh karena itu, kita lakukan perkalian terlebih dahulu:

$\displaystyle \begin{pmatrix} -4 & 6 & -10 \\[1.1ex] -2 & -8 & 0 \\[1.1ex] 6 & -4 & 10 \end{pmatrix}+\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} - \begin{pmatrix} 18 & 0 & 6 \\[1.1ex] -9 & 12 & 3 \\[1.1ex] 9 & 6 & 21 \end{pmatrix}$

Kami menambahkan dua matriks pertama:

$\displaystyle \begin{pmatrix} 1 & 6 & -10 \\[1.1ex] -2 & -3 & 0 \\[1.1ex] 6 & -4 & 15 \end{pmatrix}-\begin{pmatrix} 18 & 0 & 6 \\[1.1ex] -9 & 12 & 3 \\[1.1ex] 9 & 6 & 21 \end{pmatrix}$

Terakhir, kami melakukan pengurangan matriks:

$\displaystyle \begin{pmatrix} \bm{-17} & \bm{6} & \bm{-16} \\[1.1ex] \bm{7} & \bm{-15} & \bm{-3} \\[1.1ex] \bm{-3} & \bm{-10} & \bm{-6} \end{pmatrix}$

Jika latihan tentang perkalian skalar matriks ini bermanfaat bagi Anda, jangan ragu untuk berlatih dengan latihan yang diselesaikan langkah demi langkah tentang penjumlahan matriks dan hasil kali matriks , dua jenis operasi matriks yang akan diulangi lebih lanjut.

Sifat-sifat hasil kali suatu bilangan dengan matriks

Seperti yang telah anda ketahui, ada banyak jenis matriks : matriks persegi, matriks segitiga, matriks identitas, dll. Namun untungnya, semua sifat hasil kali bilangan dengan matriks berlaku untuk semua kelas matriks.

Berikut sifat-sifat perkalian antara skalar dan matriks:

Properti asosiatif:

$a \cdot (b \cdot A) = (a \cdot b) \cdot A$

Perhatikan dua operasi berikut karena keduanya memberikan hasil yang sama tidak peduli bagaimana kita mengalikan 2 dan 3:

$\displaystyle 2 \cdot \left(3 \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} \right) =2 \cdot \begin{pmatrix} 3 & 0 \\[1.1ex] 6 & -3 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{0} \\[1.1ex] \bm{12} & \bm{-6} \end{pmatrix}$

$\displaystyle (2 \cdot 3) \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} =6 \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{0} \\[1.1ex] \bm{12} & \bm{-6} \end{pmatrix}$

Sifat distributif terhadap penjumlahan skalar:

$(a+b) \cdot A = a \cdot A+ b \cdot A$

Seperti terlihat pada contoh di bawah, sama saja jika kita menjumlahkan 1+2 terlebih dahulu kemudian mengalikannya dengan matriks, atau jika kita mengalikan matriks secara terpisah dengan 1 dan 2 kemudian dijumlahkan hasilnya:

$\displaystyle (1 + 2) \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix} =3 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}= \begin{pmatrix} \bm{6} & \bm{-3} \\[1.1ex] \bm{9} & \bm{15} \\[1.1ex] \bm{-6} & \bm{-12} \end{pmatrix}$

$\displaystyle 1 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix} + 2 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4\end{pmatrix} = \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5\\[1.1ex] -2 & -4 \end{pmatrix} + \begin{pmatrix} 4 & -2 \\[1.1ex] 6 & 10 \\[1.1ex] -4 & -8\end{pmatrix}= \begin{pmatrix} \bm{6} & \bm{-3} \\[1.1ex] \bm{9} & \bm{15} \\[1.1ex] \bm{-6} & \bm{-12} \end{pmatrix}$

Sifat distributif terhadap penjumlahan matriks:

$a \cdot \left(A + B \right) = a \cdot A + a \cdot B$

Dengan kata lain, menjumlahkan dua matriks matematika lalu mengalikannya dengan suatu bilangan sama dengan mengalikan kedua matriks tersebut secara terpisah dengan bilangan yang sama lalu menjumlahkan hasilnya. Pada contoh di bawah ini Anda dapat memeriksa:

$\displaystyle 4 \cdot \left( \begin{pmatrix} 3 & -2 \\[1.1ex] 6 & -1 \end{pmatrix}+\begin{pmatrix} -1 & 3 \\[1.1ex] 0 & 4 \end{pmatrix} \right) =4 \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 6 & 3 \end{pmatrix}= \begin{pmatrix} \bm{8} & \bm{4} \\[1.1ex] \bm{24} & \bm{12} \end{pmatrix}$

$\displaystyle 4 \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 6 & -1 \end{pmatrix}+ 4 \cdot \begin{pmatrix} -1 & 3 \\[1.1ex] 0 & 4 \end{pmatrix} = \begin{pmatrix} 12 & -8 \\[1.1ex] 24 & -4 \end{pmatrix}+\begin{pmatrix} -4 & 12 \\[1.1ex] 0 & 16 \end{pmatrix} = \begin{pmatrix} \bm{8} & \bm{4} \\[1.1ex] \bm{24} & \bm{12} \end{pmatrix}$

Properti elemen netral:

$1 \cdot A = A$

Oleh karena itu, ketika mengalikan suatu matriks dengan 1, kita tidak mengubah matriks tersebut:

$\displaystyle 1 \cdot \begin{pmatrix} 5 & -4 & 0 \\[1.1ex] 1 & 3 & -3 \\[1.1ex] 2 & 9 & 4 \end{pmatrix}=\begin{pmatrix} \bm{5} & \bm{-4} & \bm{0} \\[1.1ex] \bm{1} & \bm{3} & \bm{-3} \\[1.1ex] \bm{2} & \bm{9} & \bm{4} \end{pmatrix}$

Ini semua adalah sifat-sifat hasil kali skalar dan matriks, jadi itulah akhir artikel ini. Kami harap Anda menyukainya dan, yang terpenting, Anda mempelajari cara menyelesaikan perkalian bilangan dengan matriks.

Di sisi lain, operasi matriks lain yang terkait dengan perkalian, dan yang sangat berguna, adalah pangkat. Di sini kami meninggalkan Anda halaman di mana Anda akan mempelajari apa itu dan bagaimana menyelesaikan pangkat matriks , jika Anda penasaran.

Mengalikan suatu bilangan dengan matriks

Bagaimana cara mengalikan suatu bilangan dengan matriks?

Contoh:

Menyelesaikan masalah perkalian suatu bilangan dengan matriks

Latihan 1:

Latihan 2:

Latihan 3:

Latihan 4:

Sifat-sifat hasil kali suatu bilangan dengan matriks

Tinggalkan Komentar Batalkan Balasan