Cara menghitung penjumlahan dan pengurangan matriks

Pada halaman ini kita akan melihat cara menjumlahkan dan mengurangkan matriks . Anda juga memiliki contoh yang akan membantu Anda memahaminya dengan sempurna dan menyelesaikan latihan sehingga Anda dapat berlatih. Anda juga akan menemukan semua properti penjumlahan matriks.

Bagaimana cara menjumlahkan dan mengurangkan matriks?

Untuk menghitung penjumlahan (atau pengurangan) dua matriks, Anda harus menjumlahkan (atau mengurangi) elemen-elemen yang menempati posisi yang sama dalam matriks-matriks tersebut.

Contoh:

contoh penjumlahan dan pengurangan matriks 2x2, operasi dengan matriks

Perhatikan bahwa untuk menjumlahkan atau mengurangkan dua matriks, keduanya harus mempunyai dimensi yang sama. Misalnya, matriks berikut tidak dapat dijumlahkan karena matriks pertama berukuran 2×2 dan matriks kedua berukuran 3×2:

\displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 0 & 2 \end{pmatrix} + \begin{pmatrix} 5 & 6 \\[1.1ex] -2 & 4 \\[1.1ex] 7 & 1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}}

Latihan soal penjumlahan dan pengurangan matriks

Latihan 1

Hitunglah jumlah matriks 2×2 berikut:

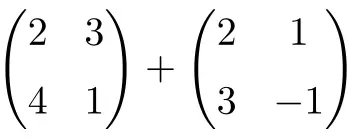
latihan diselesaikan selangkah demi selangkah untuk penjumlahan matriks 2x2

Ini adalah jumlah dari dua matriks persegi berdimensi 2×2:

\displaystyle \begin{pmatrix} 2 & 3 \\[1.1ex] 4 & 1 \end{pmatrix} + \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} = \begin{pmatrix} 2+2 & 3+1 \\[1.1ex] 4+3 & 1+(-1) \end{pmatrix} = \begin{pmatrix} \bm{4} & \bm{4} \\[1.1ex] \bm{7} & \bm{0} \end{pmatrix}

Latihan 2

Lakukan pengurangan matriks berikut:

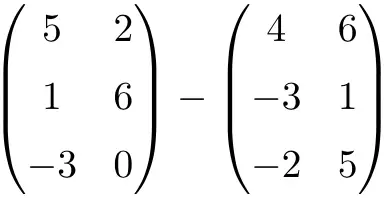
latihan diselesaikan langkah demi langkah pengurangan matriks, operasi dengan matriks

Ini adalah pengurangan dua matriks berdimensi 3×2:

\displaystyle \begin{pmatrix} 5 & 2 \\[1.1ex] 1 & 6 \\[1.1ex] -3 & 0 \end{pmatrix} - \begin{pmatrix} 4 & 6 \\[1.1ex] -3 & 1 \\[1.1ex]-2 & 5 \end{pmatrix} = \begin{pmatrix} 5-4 & 2-6 \\[1.1ex] 1-(-3) & 6-1 \\[1.1ex] -3-(-2) & 0-5 \end{pmatrix} = \begin{pmatrix} \bm{1}& \bm{-4} \\[1.1ex] \bm{4} & \bm{5} \\[1.1ex] \bm{-1} & \bm{-5} \end{pmatrix}

Latihan 3

Carilah hasil penjumlahan matriks berdimensi 3×3 berikut:

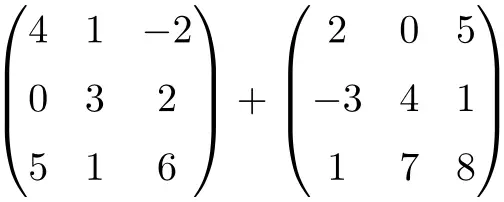
latihan diselesaikan langkah demi langkah penjumlahan matriks 3x3, operasi dengan matriks

Ini adalah jumlah dari dua matriks persegi berorde 3×3:

\displaystyle \begin{pmatrix} 4 & 1 & -2 \\[1.1ex] 0 & 3 & 2 \\[1.1ex] 5 & 1 & 6 \end{pmatrix} + \begin{pmatrix} 2 & 0 & 5 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 1 & 7 & 8 \end{pmatrix} = \begin{pmatrix} 4+2 & 1+0 & -2+5 \\[1.1ex] 0+(-3) & 3+4 & 2+1 \\[1.1ex] 5+1 & 1+7 & 6+8 \end{pmatrix} = \begin{pmatrix} \bm{6}& \bm{1} & \bm{3} \\[1.1ex] \bm{-3} & \bm{7} & \bm{3} \\[1.1ex] \bm{6} & \bm{8} & \bm{14} \end{pmatrix}

Latihan 4

Hitung penjumlahan dan pengurangan matriks persegi berorde 2 berikut:

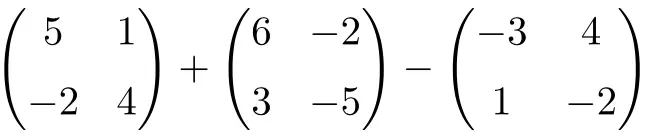
latihan diselesaikan langkah demi langkah penjumlahan dan pengurangan matriks 2x2, operasi dengan matriks

Ini adalah operasi yang digabungkan dengan penjumlahan dan pengurangan matriks persegi berorde 2:

\displaystyle \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 4 \end{pmatrix} + \begin{pmatrix} 6 & -2 \\[1.1ex] 3 & -5 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}

Jadi, pertama-tama kita jumlahkan matriks di sebelah kiri:

\displaystyle \begin{pmatrix} 11 & -1 \\[1.1ex] 1 & -1 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}

Lalu kita menghitung pengurangan matriks:

\displaystyle \begin{pmatrix} \bm{14} & \bm{-5} \\[1.1ex] \bm{0} & \bm{1} \end{pmatrix}

Latihan 5

Selesaikan penjumlahan dan pengurangan matriks berikut:

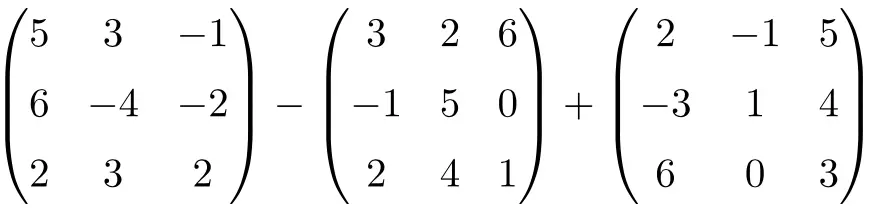
latihan diselesaikan langkah demi langkah penjumlahan dan pengurangan matriks 3x3, operasi dengan matriks

Ini adalah operasi gabungan pengurangan dan penjumlahan matriks persegi berorde 3:

\displaystyle \begin{pmatrix}5 & 3 & -1 \\[1.1ex] 6 & -4 & -2 \\[1.1ex] 2 & 3 & 2 \end{pmatrix}-\begin{pmatrix} 3 & 2 & 6 \\[1.1ex]-1 & 5 & 0 \\[1.1ex] 2 & 4 & 1 \end{pmatrix} + \begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}

Pertama, kita selesaikan pengurangan matriks:

\displaystyle \begin{pmatrix}2 & 1 & -7 \\[1.1ex] 7 & -9 & -2 \\[1.1ex] 0 & -1 & 1 \end{pmatrix}+\begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}

Dan terakhir kita menjumlahkan matriksnya:

\displaystyle \begin{pmatrix} \bm{4} & \bm{0} & \bm{-2} \\[1.1ex] \bm{4} & \bm{-8} & \bm{2} \\[1.1ex] \bm{6} & \bm{-1} & \bm{4} \end{pmatrix}

Sekarang setelah Anda mengetahui cara menjumlahkan dan mengurangkan matriks, inilah saat yang tepat untuk melihat cara mengalikan matriks , yang tentunya merupakan operasi matriks yang paling penting. Anda juga akan menemukan latihan perkalian matriks langkah demi langkah yang diselesaikan sehingga Anda dapat berlatih, seperti di semua halaman situs ini. 😉

Tambahkan Properti Matriks

Penjumlahan matriks mempunyai ciri-ciri sebagai berikut:

  • Penjumlahan matriks mempunyai sifat komutatif :

\displaystyle A +B = B + A

Oleh karena itu, urutan penjumlahan matriksnya adalah sama. Untuk mendemonstrasikannya, kita akan menjumlahkan dua matriks dengan mengubah urutannya dan Anda akan melihat hasilnya sama.

Oleh karena itu kami melanjutkan untuk menambahkan dua matriks dalam urutan tertentu:

\displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix} + \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}

Perhatikan bahwa jika kita membalikkan urutan penjumlahan matriks, hasilnya tetap sama:

\displaystyle \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix} + \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}

  • Sifat lain penjumlahan matriks adalah sifat elemen lawannya:

\displaystyle A + (-A) =0

Dengan kata lain, jika kita menjumlahkan sebuah matriks ditambah matriks yang sama tetapi semua elemennya berubah tanda, hasilnya adalah matriks nol:

\displaystyle \begin{pmatrix} 4 & 1 & -3 \\[1.1ex] 2 & 0 & 9 \end{pmatrix} + \begin{pmatrix} -4 & -1 & 3 \\[1.1ex] -2 & 0 & -9 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0} & \bm{0} \end{pmatrix}

  • Penjumlahan matriks juga mempunyai sifat elemen netral:

\displaystyle A + 0 =A

Properti ini adalah yang paling jelas, mengacu pada fakta bahwa setiap matriks ditambah matriks yang penuh dengan nol setara dengan matriks yang sama:

\displaystyle \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -3 & 4 & 9 \\[1.1ex] 1 & 12 & 6 \end{pmatrix} + \begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{1} & \bm{5} \\[1.1ex] \bm{-3} & \bm{4} & \bm{9} \\[1.1ex] \bm{1} & \bm{12} & \bm{6} \end{pmatrix}

  • Penjumlahan matriks mempunyai sifat asosiatif:

\displaystyle\left( A + B \right) + C =A + \left( B + C \right)

Oleh karena itu, urutan penjumlahan matriksnya adalah sama. Perhatikan contoh berikut, dimana kita menjumlahkan 3 matriks dengan orde berbeda dan hasilnya sama:

\displaystyle A = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} \qquad B = \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \qquad C = \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix}

\begin{aligned}\left( A + B \right) + C & =\left( \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \right) + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & = \begin{pmatrix} 6 \\[1.1ex] 0 \end{pmatrix} + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{9} \\[1.1ex] \bm{0} \end{pmatrix} \end{aligned}

\begin{aligned} A + \left( B + C \right) & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \left( \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} +\begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \right) \\[2ex] & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 7 \\[1.1ex] -1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{9} \\[1.1ex] \bm{0}\end{pmatrix} \end{aligned}

Tinggalkan Komentar

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *

Scroll to Top