Garis tegak lurus (tegak lurus) -

Di halaman ini Anda akan menemukan segala sesuatu tentang garis tegak lurus: apa itu garis, dua garis tegak lurus, cara menghitung garis tegak lurus satu sama lain, sifat-sifatnya,… Selain itu, Anda akan dapat melihat contoh dan Anda akan dapat berlatih dengan latihan yang diselesaikan langkah demi langkah.

Apa yang dimaksud dengan dua garis yang tegak lurus?

Dalam matematika, dua garis tegak lurus jika berpotongan di suatu titik membentuk empat sudut siku-siku yang sama besar (90º).

Selain itu, vektor arah dua garis yang tegak lurus juga harus tegak lurus.

Garis tegak lurus dua garis pada umumnya ditunjukkan dengan simbol

$\perp .$

Sebaliknya, perlu diingat bahwa pada bidang terdapat 4 kemungkinan dalam konsep kedudukan relatif antara dua garis: dua garis dapat berupa garis potong, tegak lurus, berhimpitan, atau sejajar. Jika mau, Anda dapat memeriksa arti setiap jenis garis di website kami.

Bagaimana cara mengetahui dua garis tegak lurus?

Ada dua cara untuk menentukan tegak lurus dua garis, yaitu dari vektor arahnya atau kemiringannya . Di bawah ini Anda memiliki penjelasan dari kedua metode tersebut, meskipun keduanya memiliki tujuan yang sama, kami menyarankan Anda mengetahui cara melakukan kedua prosedur tersebut karena masing-masing prosedur bergantung pada bagaimana garis diekspresikan.

Dari vektor arah garis

Salah satu cara untuk mengetahui tegak lurus dua garis adalah dengan menggunakan vektor arah garis yang bersangkutan. Ingatlah bahwa vektor arah adalah vektor yang menunjukkan arah suatu garis.

Vektor arah dua garis yang tegak lurus juga saling ortogonal. Oleh karena itu, jika hasil kali titik vektor-vektor arah dua garis sama dengan 0, berarti garis-garis tersebut tegak lurus.

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s =0 \quad \longrightarrow \quad r \perp s$

Mari kita lihat bagaimana tegak lurus dua garis ditentukan dengan menggunakan contoh:

$\displaystyle r: \ \begin{cases} x=3-2t \\[2ex] y=6+3t \end{cases}\qquad \qquad s: \ \begin{cases} x=4+3t \\[2ex] y=-2+2t \end{cases}$

Kedua garis tersebut dinyatakan sebagai persamaan parametrik, sehingga komponen vektor arah setiap garis adalah angka di depan parameternya.

$t:$

$\vv{\text{v}}_r =(-2,3) \qquad \qquad \vv{\text{v}}_s=(3,2)$

Setelah kita mengetahui vektor arah setiap garis, kita memeriksa apakah garis tersebut tegak lurus dengan menghitung hasil kali antara vektor-vektor tersebut:

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = (-2,3)\cdot (3,2) = -2\cdot 3 +3\cdot 2= \bm{0}$

Hasil kali titik kedua vektor adalah nol, sehingga garis-garisnya tegak lurus.

Kemiringan garis

Cara lain untuk menentukan apakah dua garis tegak lurus adalah dengan menggunakan kemiringannya. Ingatlah bahwa kemiringan suatu garis adalah koefisiennya

$m$

persamaan eksplisit dan persamaan titik-kemiringan suatu garis.

$y=mx+n \qquad \qquad y-y_0=m(x-x_0)$

Dan kemiringan suatu garis juga dapat diperoleh dari koefisien

$A$

Dan

$B$

dari persamaan garis implisit (atau umum):

$Ax+By+C= 0 \ \longrightarrow \ m = -\cfrac{A}{B}$

Jadi, gradien dua garis yang tegak lurus adalah berbanding terbalik dan berlawanan tanda, artinya persamaan berikut selalu terpenuhi:

$r \perp s \quad \longrightarrow \quad m_r=-\cfrac{1}{m_s}$

Jadi , jika hasil kali gradien dua garis berbeda sama dengan -1, berarti kedua garis tersebut tegak lurus:

$m_r\cdot m_s=-1\quad \longrightarrow \quad r \perp s$

Misalnya, dua garis berikut ini tegak lurus:

$r: \ y=2x+4 \qquad \qquad s: \ y=-\cfrac{1}{2} \ x-5$

Dapat kita tunjukkan bahwa keduanya adalah dua garis yang saling tegak lurus dari lerengnya. Kemiringan tiap garis adalah:

$m_r = 2 \quad \quad m_s=-\cfrac{1}{2}$

Sekarang kita kalikan kemiringannya:

$\displaystyle 2 \cdot \left(-\frac{1}{2} \right) = -\cfrac{2}{2} = \bm{-1}$

Hasil kali antara kedua lereng sama dengan -1, yang berarti dua garis tegak lurus satu sama lain.

Bagaimana cara menghitung garis yang tegak lurus dengan garis lainnya?

Walaupun kelihatannya sulit untuk dilakukan, mencari garis yang tegak lurus terhadap garis lain cukup sederhana, untuk itu Anda hanya memerlukan vektor arah yang tegak lurus garis dan titik yang termasuk dalam garis tersebut.

Satu-satunya kesulitan adalah, seperti sebelumnya, prosedurnya bergantung pada jenis persamaan yang menyatakan garis. Karena suatu garis yang tegak lurus satu sama lain dapat dihitung dari vektor arah atau dari lerengnya .

Dari vektor arah ke kanan

Sebuah garis yang tegak lurus terhadap garis lain dapat dicari dengan menggunakan vektor arahnya. Mari kita lihat bagaimana hal ini dilakukan dengan sebuah contoh:

Hitunglah garis yang tegak lurus terhadap garis tersebut
$r$

apa yang melewati titik tersebut

$P(5,-1)$

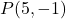
. menjadi lurus

$r:$

$\displaystyle r : \ 3x+2y-1=0$

Hal pertama yang perlu kita lakukan adalah mengidentifikasi vektor arah garis. Dalam hal ini garis didefinisikan dalam bentuk persamaan umum (atau implisit), oleh karena itu koordinat kartesius dari vektor arah garis dapat diperoleh dengan koefisien A dan B garis:

$\vv{\text{v}}_r =(-B,A)=(-2,3)$

Dan setelah kita mengetahui vektor arah suatu garis, kita harus menghitung vektor yang tegak lurus garis tersebut. Untuk melakukan ini, cukup masukkan koordinat vektor dan ubah tanda salah satunya (yang Anda inginkan):

$\vv{\text{v}}_\perp =(3,2)$

Jadi sekarang kita mengetahui vektor arah garis. Oleh karena itu, persamaan garis implisitnya adalah sebagai berikut:

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}_\perp= (3,2) \end{array} \right\}\longrightarrow \begin{array}{l}A=2 \\[2ex] B=-3 \end{array}$

$Ax+By+C \ \longrightarrow \ 2x-3y+C=0$

Oleh karena itu, cukup menentukan parameter C. Untuk melakukannya, kita substitusikan titik milik garis lurus ke dalam persamaannya dan selesaikan persamaan yang dihasilkan:

$P(5,-1)$

$2x-3y+C=0 \ \xrightarrow{x=5 \ ; \ y=-1} \ 2\cdot 5-3\cdot (-1)+C=0$

$10+3+C=0$

$13+C=0$

$C=-13$

Kesimpulannya, persamaan garis tegak lurus adalah:

$\bm{2x-3y-13=0}$

Dari kemiringan garis

Cara lain untuk mencari garis yang tegak lurus suatu garis adalah dengan melihat kemiringannya. Mari kita lihat bagaimana masalah jenis ini diselesaikan melalui sebuah contoh:

Hitunglah garis yang tegak lurus terhadap garis tersebut
$r$

apa yang melewati titik tersebut

$P(0,1)$

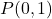
. menjadi lurus

$r:$

$\displaystyle r : \ y=4x-3$

Kemiringan garis

$r$

Timur:

$m_r = 4$

Setelah kita mengetahui kemiringan garis, kita perlu mencari kemiringan garis yang tegak lurus tersebut. Seperti yang kita lihat pada bagian di atas, kemiringan dua garis tegak lurus adalah berbanding terbalik dan tandanya berubah. Oleh karena itu, untuk menentukan kemiringan garis tegak lurus, kita perlu membalikkan kemiringan yang diperoleh dan mengubah tandanya:

$m_\perp =-\cfrac{1}{4}$

Oleh karena itu, persamaan eksplisit garis tegak lurus adalah sebagai berikut:

$y= mx+n$

$y=-\cfrac{1}{4} \ x + n$

Terakhir, kita menghitung ordinat titik asal garis tegak lurus dengan mensubstitusikan koordinat titik tersebut ke dalam persamaan garis:

$P(0,1)$

$y=-\cfrac{1}{4} \ x + n \ \xrightarrow{x=0 \ ; \ y=1} \ 1 =-\cfrac{1}{4}\cdot 0 + n$

$1 = n$

Singkatnya, persamaan garis tegak lurus adalah:

$\bm{y=-}\mathbf{\cfrac{1}{4}} \ \bm{x + 1}$

Sifat-sifat garis tegak lurus

Semua garis tegak lurus mempunyai ciri-ciri sebagai berikut:

Hubungan simetris : Jika suatu garis tegak lurus terhadap garis lain, maka garis tersebut juga tegak lurus terhadap garis pertama.

$r \bm{\perp} s \ \longrightarrow \ s \bm{\perp} r$

Sifat non-refleksif : Jelas, tidak ada garis yang tegak lurus terhadap dirinya sendiri.

$r \ \cancel{\bm{\perp}}} \ r$

Teorema: Dalam geometri Euclidean (dalam R2), setiap pasangan garis yang tegak lurus terhadap garis ketiga harus sejajar. Artinya, jika suatu garis tegak lurus terhadap garis lain dan garis tersebut juga tegak lurus terhadap garis ketiga, maka garis pertama dan terakhir sejajar.

Menyelesaikan masalah garis tegak lurus

Latihan 1

Garis manakah di bawah ini yang tegak lurus terhadap garis tersebut

$r: y=3x+4$

$a : \ y=3x-\cfrac{1}{3}$

$b : \ y=-\cfrac{1}{3} \ x+5$

$c : \ y=-4x-3$

$d : \ y=\cfrac{1}{3} \ x-5$

$e : \ y=-\cfrac{1}{3} \ x-2$

lihat solusi

Kemiringan garis

$r$

adalah 3:

$m_r=3$

Dan kemiringan dua garis yang tegak lurus adalah berbanding terbalik dan berlawanan tanda, maka kemiringan setiap garis yang tegak lurus terhadap garis tersebut adalah

$r$

harus:

$m_\perp=-\cfrac{1}{3}$

Sehingga garisnya tegak lurus terhadap garis tersebut

$r$

adalah mereka yang kemiringannya sama dengan

$-\cfrac{1}{3}$

. Artinya, garis-garisnya

$\bm{b}$

Dan

$\bm{e}.$

Latihan 2

Tentukan apakah dua garis berikut tegak lurus:

$\displaystyle r: \ \begin{cases} x=4-t \\[2ex] y=1-3t \end{cases}\qquad \qquad s: \ \cfrac{x-2}{4} = \cfrac{y+3}{6}$

lihat solusi

hak

$r$

dinyatakan dalam bentuk persamaan parametrik, sehingga komponen vektor arah garis tersebut adalah bilangan di depan parameternya.

$t:$

$\vv{\text{v}}_r =(-1,-3)$

Sebaliknya garis lurus

$s$

didefinisikan dalam bentuk persamaan kontinu, sehingga koordinat vektor arahnya adalah bilangan penyebutnya:

$\vv{\text{v}}_s =(4,6)$

Setelah kita mengetahui vektor arah setiap garis, kita dapat memeriksa apakah garis tersebut tegak lurus dengan menghitung hasil kali kedua vektor tersebut:

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = (-1,-3)\cdot (4,6) = -1\cdot 4 + (-3)\cdot 6= -22 \bm{\neq 0}$

Hasil kali titik kedua vektor adalah bukan nol, sehingga garis-garisnya tidak tegak lurus .

Latihan 3

Temukan garis yang tegak lurus terhadap garis tersebut

$r$

apa yang melewati titik tersebut

$P(-2,1)$

. menjadi lurus

$r:$

$\displaystyle r : \ 4x-y+5=0$

lihat solusi

Hal pertama yang perlu kita lakukan adalah mengidentifikasi vektor arah garis. Dalam hal ini garis didefinisikan dalam bentuk persamaan umum (atau implisit), sehingga vektor arahnya adalah:

$\vv{\text{v}}_r =(-B,A)=(1,4)$

Setelah kita mengetahui vektor arah suatu garis, kita perlu menghitung vektor yang tegak lurus garis tersebut. Untuk melakukan ini, cukup masukkan koordinat vektor dan ubah tanda salah satunya (yang Anda inginkan):

$\vv{\text{v}}_\perp =(4,-1)$

Oleh karena itu, persamaan garis implisitnya adalah sebagai berikut:

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}_\perp= (4,-1) \end{array} \right\}\longrightarrow \begin{array}{l}A=-1 \\[2ex] B=-4 \end{array}$

$Ax+By+C \ \longrightarrow \ -x-4y+C=0$

Oleh karena itu, cukup menentukan C yang tidak diketahui. Untuk melakukannya, kita substitusikan titik yang dilalui garis tersebut ke dalam persamaannya:

$P(-2,1)$

$-x-4y+C=0 \ \xrightarrow{x=-2 \ ; \ y=1} \ -(-2)-4\cdot 1+C=0$

$2-4+C=0$

$-2+C=0$

$C=2$

Akhirnya persamaan garis tegak lurusnya adalah:

$\bm{-x-4y+2=0}$

Latihan 4

Temukan persamaan titik-kemiringan garis yang tegak lurus garis tersebut

$r$

apa yang melewati titik tersebut

$P(3,-2)$

. menjadi lurus

$r:$

$\displaystyle r : \ y=5x+1$

lihat solusi

Kemiringan garis

$r$

Timur:

$m_r = 5$

Setelah kita mengetahui kemiringan garis, kita perlu mencari kemiringan garis yang tegak lurus tersebut. Untuk melakukan ini, cukup balikkan kemiringan yang ditemukan dan ubah tandanya:

$m_\perp =-\cfrac{1}{5}$

Terakhir, cukup substitusikan kemiringan yang ditemukan dan koordinat titik ke dalam persamaan kemiringan titik garis:

$y -y_0=m(x-x_0)$

$y-(-2)=-\cfrac{1}{5} (x- 3)$

$\bm{y+2=}\mathbf{-\cfrac{1}{5}}\bm{ (x- 3)}$

Latihan 5

hak

$r$

melewati titik (2,1) dan (4,2), dan garis

$s$

melewati titik (-1,2) dan (1,-2). Tentukan apakah kedua garis tersebut tegak lurus atau tidak.

lihat solusi

Untuk memeriksa apakah ini adalah dua garis yang tegak lurus, kita akan menghitung kemiringannya dan kemudian melihat apakah kedua garis tersebut menghormati hubungan tegak lurus tersebut. Ingatlah bahwa rumus kemiringan suatu garis adalah:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

Kemiringan garis

$r$

Timur:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{2-1}{4-2} = \cfrac{1}{2}$

Kemiringan garis

$s$

Timur:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{-2-2}{1-(-1)} = \cfrac{-4}{2}=-2$

Untuk memeriksa tegak lurus kedua garis, kita harus melihat apakah kemiringan suatu garis merupakan kebalikan dari kemiringan garis lainnya. Dalam hal ini kedua lereng tersebut berbanding terbalik dan juga mempunyai tanda yang berlawanan, sehingga kedua garis tersebut saling tegak lurus.

Latihan 6

Hitung nilai dari

$k$

sehingga dua garis berikut tegak lurus:

$\displaystyle r: \ 5x+3y-7=0\qquad \qquad s: \ 4x+ky+1=0$

lihat solusi

Kedua garis tersebut dinyatakan dalam bentuk persamaan implisit (atau umum), dan vektor arah persamaan garis implisit adalah:

$Ax+By+C=0$

$\vv{\text{v}} =(-B,A)$

Oleh karena itu, vektor arah setiap garis adalah:

$\vv{\text{v}}_r =(-3,5) \qquad \qquad \vv{\text{v}}_s =(-k,4)$

Agar dua garis tegak lurus, hasil kali skalar vektor arahnya harus sama dengan nol. Oleh karena itu, kami akan menerapkan kondisi ini untuk mencari nilai yang tidak diketahui

$k:$