Garis paralel - Mathority

Di sini Anda akan menemukan segala sesuatu tentang garis sejajar: apa artinya, cara menentukan apakah dua garis sejajar, sifat-sifatnya, dll. Selain itu, Anda akan dapat melihat beberapa contoh dan penyelesaian latihan garis sejajar.

Apa itu garis sejajar?

Garis sejajar adalah garis yang tidak pernah berpotongan, artinya meskipun lintasannya diperpanjang hingga tak terhingga, garis tersebut tidak akan pernah bersentuhan satu sama lain. Oleh karena itu, titik-titik pada dua garis sejajar selalu berjarak sama satu sama lain, dan terlebih lagi, dua garis sejajar tidak mempunyai titik yang sama.

Misalnya, dua garis berikut ini sejajar:

Secara umum kita menunjukkan bahwa dua garis sejajar dengan 2 batang vertikal || yang tersirat

Sebaliknya, meskipun dua garis sejajar tidak pernah berpotongan, dalam geometri analitik dikatakan keduanya membentuk sudut 0º karena arahnya sama.

Kapan dua garis sejajar?

Setelah kita mengetahui pengertian garis sejajar, kita akan mengetahui cara mencari dua garis sejajar. Tentu saja salah satu caranya adalah dengan membuat grafik garis-garis tersebut dan melihat apakah garis-garis tersebut berpotongan pada grafik, namun ada metode yang lebih sederhana dan mudah digunakan.

Tentukan kesejajaran dua garis dengan gradiennya

Anda dapat mengetahui letak dua garis sejajar dengan melihat kemiringan setiap garis. Ingatlah bahwa kemiringan suatu garis adalah parameternya

$m$

dari persamaan eksplisit dan persamaan titik-kemiringan garis:

$y=mx+n \qquad \qquad y-y_0=m(x-x_0)$

Namun ada beberapa cara untuk menentukan kemiringan suatu garis, maka untuk mengetahui cara menghitungnya, kami sarankan untuk melihat rumus kemiringan suatu garis . Selain itu, pada halaman tertaut Anda juga akan menemukan penjelasan tentang apa yang diwakili oleh kemiringan suatu garis dan mengapa hal itu sangat penting bagi sebuah garis.

Jadi, pada suatu bidang, dua garis dikatakan sejajar jika mempunyai kemiringan (koefisien m) yang sama dan ordinat yang berbeda di titik asal (koefisien n) .

Misalnya, dua garis berikut ini sejajar:

$r: \ y=5x+1 \qquad \qquad s: \ y=5x-3$

Kedua garis tersebut merupakan dua garis sejajar karena keduanya mempunyai kemiringan yang sama dan terlebih lagi suku-suku bebasnya berbeda.

$m_r =m_s =5$

$n_r =1 \neq n_s =-3$

Perlu dicatat bahwa jika dua garis memiliki kemiringan yang sama dan pada saat yang sama komputer yang sama berada di titik asal, maka kedua garis tersebut akan menjadi garis yang identik karena keduanya akan persis sama.

Temukan paralelisme dua garis dari persamaan implisit

Ingatlah bahwa persamaan garis implisit (atau umum) adalah:

$Ax+By+C=0$

Jadi, jika koefisien A dan B dua garis sebanding satu sama lain tetapi tidak sebanding dengan koefisien C , berarti kedua garis tersebut sejajar.

$r: \ Ax+By+C=0 \qquad \qquad s: \ A'x+B'y+C'=0$

$\cfrac{A}{A'} = \cfrac{B}{B'} \neq \cfrac{C}{C'} \quad \bm{\longrightarrow} \quad r \parallel s$

Berikut dua garis sejajar yang dinyatakan dalam bentuk persamaan umum (atau implisit):

$r: \ 4x-6y+7=0 \qquad \qquad s: \ -2x+3y-1=0$

Mereka sejajar karena angka-angka di depan variabel

$x$

sebanding dengan angka di depan variabel

$y$

, tetapi tidak dengan persyaratan independen.

$\cfrac{4}{-2} = \cfrac{-6}{3} = -2 \neq \cfrac{7}{-1}=-7$

Seperti sebelumnya, jika semua koefisien (A, B, dan C) dari dua garis implisit adalah proporsional, hal ini berarti kedua garis tersebut berimpit, atau dengan kata lain keduanya sama besar.

Sifat-sifat garis sejajar

Ciri-ciri garis sejajar adalah sebagai berikut:

Sifat simetris : jika suatu garis sejajar dengan garis lainnya, maka garis tersebut juga sejajar dengan garis pertama. Sifat ini juga dimiliki oleh garis tegak lurus.

$r \parallel s \ \longrightarrow \ s \parallel r$

Sifat transitif : jika suatu garis sejajar dengan garis lain, dan garis kedua sejajar dengan garis ketiga, maka garis pertama juga sejajar dengan garis ketiga.

$\left. \begin{array}{c} r \parallel s\\[2ex] s \parallel q \end{array} \right\} \longrightarrow \ r \parallel q$

Hasil kali skalar vektor-vektor arah (vektor yang menunjukkan arah suatu garis) dari dua garis sejajar sama dengan hasil kali modul-modulnya.

$r \parallel s \ \longrightarrow \ \vv{\text{v}}_r \cdot \vv{\text{v}}_s= \lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{\text{v}}_s \rvert$

Selain itu, vektor arah dua garis sejajar selalu bergantung linier satu sama lain karena proporsional .

Kondisi ini diperlukan agar garis sejajar tetapi tidak cukup, atau dengan kata lain, dua garis sejajar harus mempunyai vektor arah yang sebanding, tetapi kenyataan bahwa dua garis mempunyai vektor arah yang sebanding tidak secara langsung berarti bahwa kedua garis tersebut sejajar. Karena garis-garis yang berhimpitan juga mempunyai vektor-vektor arah yang sebanding.

Garis yang sejajar sumbu absis (sumbu X) bersifat horizontal dan selalu berbentuk
$y=k.$

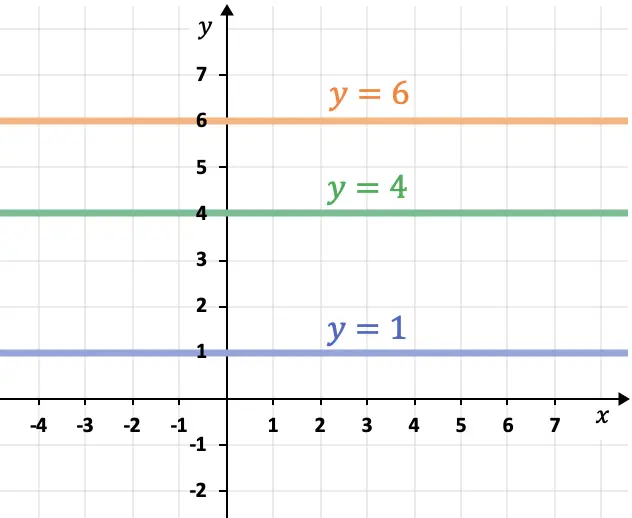
Garis yang sejajar dengan sumbu komputer (sumbu Y) bersifat vertikal dan selalu mengikuti ekspresi
$x=k.$

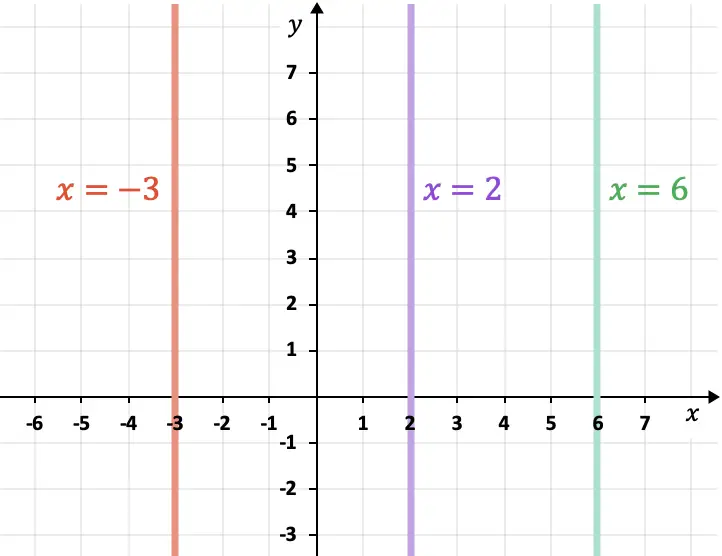
Cara menghitung jarak antara dua garis sejajar pada bidang datar

Untuk mencari jarak antara dua garis sejajar pada bidang (dalam R2), cukup ambil sebuah titik pada salah satu dari dua garis tersebut dan hitung jarak dari titik tersebut ke garis lainnya.

Kita dapat melakukannya dengan cara ini karena dua garis sejajar selalu berjarak sama.

Sebaliknya, jika dengan menggunakan rumus diperoleh jarak 0 satuan, berarti garis-garis tersebut saling bersentuhan di suatu titik sehingga garis-garis tersebut tidak sejajar, melainkan berpotongan, berhimpitan, atau tegak lurus. Jika mau, Anda dapat memeriksa perbedaan jenis garis ini di website kami.

Nah, agar Anda dapat melihat caranya, kita akan menentukan jarak antara dua garis sejajar berikut sebagai contoh:

$r: \ 2x-4y-6=0 \qquad \qquad s: \ -x+2y+4=0$

Hal pertama yang perlu kita lakukan adalah mendapatkan titik pada salah satu garis (yang Anda inginkan). Dalam hal ini, kita akan menghitung sebuah titik pada garis

$s.$

Untuk melakukan ini, kita harus memberi nilai pada salah satu variabel, yang akan kita lakukan misalnya

$x=0:$

$-x+2y+4 =0 \ \xrightarrow{x \ = \ 0} \ -0+2y+4=0$

Dan sekarang kita menghapus variabel lainnya (

$y$

) dari persamaan yang diperoleh untuk mengetahui berapa nilainya pada saat ini:

$2y=-4$

$y= \cfrac{-4}{2}$

$y= -2$

Oleh karena itu, titik diperoleh dari garis tersebut

$s$

Timur:

$P(0,-2)$

Dan setelah kita mempunyai sebuah titik pada suatu garis, kita menghitung jarak dari titik tersebut ke garis lainnya menggunakan rumus jarak dari suatu titik ke garis:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 2\cdot 0 + (-4)\cdot (-2) +(-6)\rvert}{\sqrt{2^2+(-4)^2}}= \cfrac{\lvert 0+8-6\rvert}{\sqrt{4+16}}={\cfrac{2}{\sqrt{20}}=\bm{0,45}$

Oleh karena itu, jarak antara dua garis sejajar setara dengan 0,45 satuan .

Garis Paralel Memecahkan Masalah

Latihan 1

Manakah dari garis berikut yang sejajar?

$\begin{array}{l} r: \ y=2x+3 \\[2ex] s: \ y=3x-2 \\[2ex] q: \ y=2x+6 \\[2ex] t: \ y=-2x-4\end{array}$

lihat solusi

Dua garis dikatakan sejajar jika mempunyai kemiringan yang sama (dan titik potongnya berbeda). Jadi, kemiringan tiap garis adalah:

$m_r = 2$

$m_s = 3$

$m_q = 2$

$m_t = -2$

Jadi hanya garis-garisnya saja yang sejajar

$r$

Dan

$q,$

karena hanya mereka yang memiliki kemiringan yang sama.

Latihan 2

Temukan persamaan eksplisit garis yang sejajar dengan garis tersebut

$r$

dan apa yang terjadi di titik tersebut

$P(0,2).$

menjadi lurus

$r:$

$r: \; y=3x-1$

lihat solusi

Sehingga garis tersebut sejajar dengan garis

$r,$

keduanya harus mempunyai kemiringan yang sama. dan kemiringan garis

$r$

adalah 3:

$m = 3$

Oleh karena itu, persamaan garis eksplisit yang perlu kita cari adalah:

$y=3x+n$

Dan setelah kita mengetahui kemiringan garis, kita dapat menghitung titik potong dengan mensubstitusikan titik yang termasuk dalam garis tersebut ke dalam persamaan garis:

$P(0,2)$

$y= 3x+n \ \xrightarrow{x=0 \ ; \ y=2} \ 2=3\cdot 0 +n$

$2=0+ n$

$2= n$

Jadi persamaan garisnya secara eksplisit adalah:

$\bm{y=3x+2}$

Latihan 3

Hitung nilai yang tidak diketahui

$a$

Dan

$b$

sehingga dua garis berikut sejajar:

$r: \ 2x-4y+6=0 \qquad \qquad s: \ x+ay+b=0$

lihat solusi

Garis-garis tersebut dijelaskan dalam bentuk persamaan umum (atau implisit). Oleh karena itu, agar kedua garis sejajar maka koefisien A dan Bnya harus proporsional, yaitu persamaan berikut harus dipenuhi:

$\cfrac{2}{1} = \cfrac{-4}{a}$