Pada bagian ini kita akan melihat bagaimana membahas dan menyelesaikan sistem persamaan dengan metode Gauss-Jordan . Artinya, tentukan apakah sistem tersebut merupakan sistem yang kompatibel (DCS), sistem yang kompatibel tidak tentu (ICS), atau sistem yang tidak kompatibel. Selain itu, Anda akan menemukan contoh dan latihan yang diselesaikan sehingga Anda dapat mempraktikkan dan mengasimilasi konsep dengan sempurna.
Untuk memahami apa yang akan kami jelaskan selanjutnya, penting bagi Anda untuk mengetahui cara menyelesaikan sistem menggunakan metode Gauss , jadi kami menyarankan Anda untuk melihatnya sebelum melanjutkan.
Sistem yang kompatibel ditentukan dengan metode Gauss
Selama baris terakhir matriks Gaussian adalah
![]()
, menjadi
![]()
Dan
![]()
dua angka apa pun, ini adalah SCD (System Kompatibel Ditentukan). Oleh karena itu, sistem memiliki solusi unik .
Sebagian besar sistem adalah SCD.
Contoh:
Misalnya, kami memiliki sistem ini:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 3x+8y+z=1\\[2ex] 6x+4y-z=-1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bab5d5823e45833aa691a3510a2a23eb_l3.png)
Yang matriksnya diperluas adalah:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 3x+8y+z=1\\[2ex] 6x+4y-z=-1 \end{array} \right\}} \ \longrightarrow \ \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 3 & 8 & 1 & 1 \\[2ex] 6 & 4 & -1 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f8daea11edeedfd6b86bb251fe19032_l3.png)
Untuk menyelesaikan sistem ini kita perlu mengoperasikan baris-baris matriks dan mengubah semua elemen di bawah diagonal utama menjadi 0. Jadi dari baris kedua kita kurangi baris pertama dan dari baris ketiga kita kurangi baris pertama dikalikan 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 3 & 8 & 1 & 1 \\[2ex] 6 & 4 & -1 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -f_1} \\[2ex] \xrightarrow{f_3 -2f_1} & \end{array} \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 0 & 6 & 2 & 0 \\[2ex] 0 & 0 & 1 & -3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-d68ac25745ddc71d1e7f55f68dd4ea7a_l3.png)
Setelah semua bilangan di bawah diagonal utama adalah 0, kita kembali meneruskan sistem ke dalam bentuk persamaan:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 0 & 6 & 2 & 0 \\[2ex] 0 & 0 & 1 & -3 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 6y+2z=0\\[2ex] 1z=-3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4457f1b034e72c6945bfe609eff52b9a_l3.png)
Jadi sistem ini adalah SCD , karena matriksnya digeser dan baris terakhirnya bertipe
![]()
. Oleh karena itu, kami menyelesaikannya seperti biasa: dengan menghilangkan hal-hal yang tidak diketahui dari persamaan dari bawah ke atas.
![]()
![]()
![]()
Sekarang kita tahu z, kita masukkan nilainya ke persamaan kedua untuk mencari nilai
![]()
:
![]()
![]()
![]()
![]()
![]()
Dan terakhir, kita melakukan hal yang sama dengan persamaan pertama: kita mengganti nilai-nilai yang tidak diketahui lainnya dan menyelesaikannya
![]()
:
![]()
![]()
![]()
![]()
![]()
![]()
Oleh karena itu, penyelesaian sistem persamaan tersebut adalah:
![]()
Sistem yang tidak kompatibel menurut metode Gauss
Ketika dalam matriks Gauss kita memiliki baris dengan tiga angka 0 berturut-turut dan sebuah angka
![]()
, ini adalah IS (Sistem Tidak Kompatibel), dan oleh karena itu, sistem tidak memiliki solusi .
Contoh:
Misalnya, bayangkan setelah mengoperasikan matriks Gaussian suatu sistem, kita mendapatkan:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 4 & 1 & -1 & 0 \\[2ex] 0 & 3 & 1 & -1 \\[2ex] 0 & 0 & 0 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-defe65fa616eff800314ebc6dc6f552b_l3.png)
Seperti baris terakhir
![]()
, yaitu tiga angka 0 yang diikuti angka di akhir, merupakan IF (Sistem Tidak Kompatibel) dan oleh karena itu, sistem tidak mempunyai solusi .
Meskipun tidak perlu mengetahuinya, di bawah ini Anda akan melihat mengapa tidak ada solusinya.
Jika kita mengambil baris terakhir, kita akan mendapatkan persamaan ini:
![]()
Persamaan ini tidak akan pernah terpenuhi, karena berapa pun nilai z , mengalikannya dengan 0 tidak akan pernah menghasilkan 2 (bilangan apa pun yang dikalikan 0 selalu menghasilkan 0). Dan karena persamaan ini tidak akan pernah terpenuhi, sistem tidak mempunyai solusi.
Sistem yang kompatibel belum ditentukan dengan metode Gaussian
Setiap kali baris matriks Gaussian terisi 0
![]()
, ini adalah SCI (Sistem Kompatibel Tak Tertentu), dan, oleh karena itu, sistem tersebut memiliki solusi tak terbatas .
Mari kita lihat contoh cara menyelesaikan ICS:
Contoh:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y-1z=-2 \\[2ex] 3x+4y+z=4 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-18a63dfebc1f23923714e475aad2e808_l3.png)
Seperti biasa, pertama-tama kita membuat matriks diperluas dari sistem :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y-1z=-2 \\[2ex] 3x+4y+z=4 \end{array} \right\} \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & -1 & -2 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f273040101827fdfea5c9a4858be5567_l3.png)
Sekarang kita ingin semua bilangan di bawah diagonal utama menjadi 0. Jadi, pada baris kedua kita tambahkan baris pertama dikalikan -2:
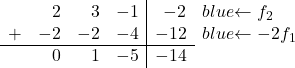
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & -1 & -2 \\[2ex] 3 & 4 & 1 & 4\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -2f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c889a6f147c6b0430731aa778121af52_l3.png)
Untuk mengubah 3 menjadi 0, pada baris ketiga kita tambahkan baris pertama dikalikan -3:
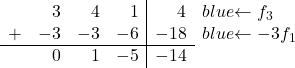
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -3f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c5acccc51108267fef6d3320068743aa_l3.png)
Untuk mengubah 1 pada baris terakhir menjadi 0, pada baris ketiga kita tambahkan baris kedua dikalikan -1:

![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -1f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a02e4819adfbe7b80d2952f87f113757_l3.png)
Karena baris terakhir semuanya 0 , kita dapat menghapusnya:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6aea469dceab08e6aa62571922eb2824_l3.png)
Dan karena seluruh baris kita diisi dengan angka 0, ini adalah SCI.
Oleh karena itu kami berakhir dengan sistem berikut:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+y+2z=6 \\[2ex] y-5z=-14 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-598c031f4cba5a865952a57ed46f0f95_l3.png)
Jika sistemnya adalah SCI, maka perlu mengambil nilai parameter dari yang tidak diketahui
![]()
. Dan kita perlu menyelesaikan sistem berdasarkan parameter ini
![]()
.
Oleh karena itu, kami menetapkan nilai
![]()
ke z :
![]()
Meskipun kita juga bisa memilih hal lain yang tidak diketahui untuk dijadikan nilai
![]()
.
Sekarang kita isolasi y dari persamaan kedua dan biarkan menjadi fungsi dari
![]()
:
![]()
![]()
![]()
Dan terakhir kita hapus x dari persamaan pertama dan biarkan juga sebagai fungsi dari
![]()
:
![]()
![]()
![]()
![]()
Oleh karena itu solusi sistemnya adalah:
![]()
Seperti yang Anda lihat, ketika sistemnya adalah SCI, kami membiarkan solusinya bergantung pada parameternya
![]()
. Dan ingatlah bahwa ia memiliki solusi tak terbatas, karena bergantung pada nilai yang dibutuhkan
![]()
, solusinya adalah salah satunya.
Sebelum melanjutkan ke latihan penyelesaian, Anda harus tahu bahwa meskipun dalam artikel ini kami menggunakan metode Gauss, cara lain untuk membahas dan menyelesaikan sistem persamaan linier adalah teorema Rouche . Faktanya, ini mungkin lebih banyak digunakan.
Latihan soal pembahasan sistem persamaan menggunakan metode Gauss-Jordan
Latihan 1
Tentukan jenis sistem apa yang terlibat dan selesaikan sistem persamaan berikut menggunakan metode Gauss:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y+5z=8 \\[2ex] 3x+3y+6z=9 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-be4ba1bd1ce7452e66c5189d995d948c_l3.png)
Hal pertama yang perlu kita lakukan adalah matriks yang diperluas dari sistem:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y+5z=8 \\[2ex] 3x+3y+6z=9 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & 5 & 8 \\[2ex] 3 & 3 & 6 & 9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b600f3fc0d79a06eb972dbacb673a780_l3.png)
Sekarang kita perlu membuat semua angka di bawah array utama menjadi 0.
Oleh karena itu kami melakukan operasi baris untuk membatalkan dua suku terakhir dari kolom pertama:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & 5 & 8 \\[2ex]3 & 3 & 6 & 9 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 2f_1} \\[2ex] \xrightarrow{f_3 - 3f_1}& \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & 1 & -4 \\[2ex] 0 & 0 & 0 & -9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a1d832d5bb115666614ae96822c360eb_l3.png)
Kami memperoleh baris matriks yang terdiri dari tiga angka 0 diikuti dengan angka. Oleh karena itu, ini adalah IS (Sistem Tidak Kompatibel) dan sistem tidak memiliki solusi.
Latihan 2
Tentukan jenis sistemnya dan carilah penyelesaian sistem persamaan berikut dengan menggunakan metode Gauss:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-2y+3z=1 \\[2ex] -2x+5y-z=5 \\[2ex] -x+3y+2z=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7f5aba495f2c6a301e923ee3c6238012_l3.png)
Hal pertama yang perlu kita lakukan adalah matriks yang diperluas dari sistem:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-2y+3z=1 \\[2ex] -2x+5y-z=5 \\[2ex] -x+3y+2z=6 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] -2 & 5 & -1 & 5 \\[2ex] -1 & 3 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f8bb5e5ab85946bddad72067fe17d937_l3.png)
Sekarang kita perlu membuat semua angka di bawah array utama menjadi 0.
Oleh karena itu kami melakukan operasi baris untuk membatalkan dua suku terakhir dari kolom pertama:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] -2 & 5 & -1 & 5 \\[2ex] -1 & 3 & 2 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 2f_1} \\[2ex] \xrightarrow{f_3 + f_1} \end{array} \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-83e48becaaa6683719ac57eb7d118943_l3.png)
Sekarang mari kita coba menghapus elemen terakhir dari kolom kedua:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -f_2} \end{array} \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-16a1afc0eb224ee5f05c9e313586854d_l3.png)
Tapi kita mendapatkan seluruh baris 0. Jadi ini adalah SCI dan sistemnya memiliki banyak sekali solusi.
Tapi karena ini adalah ICS, kita bisa menyelesaikan sistemnya berdasarkan
![]()
. Oleh karena itu kami menghapus baris 0:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-5c838c5f1b229d4c8a43ac9ddd8e3629_l3.png)
Sekarang kita nyatakan matriks tersebut dalam bentuk sistem persamaan yang tidak diketahui:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x-2y+3z=1 \\[2ex] 1y+5z=7 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b3fd941d33fec646d16b8181430c9986_l3.png)
Kami memberi nilai
![]()
Untuk
![]()
![]()
Kami mengganti nilai
![]()
dalam persamaan kedua untuk mencari nilai
![]()
![]()
![]()
![]()
Dan kita melakukan hal yang sama dengan persamaan pertama: kita mengganti nilai-nilai yang tidak diketahui lainnya dan menghapusnya
![]()
![]()
![]()
![]()
![]()
Oleh karena itu, penyelesaian sistem persamaan tersebut adalah:
![]()
Latihan 3
Temukan jenis sistemnya dan selesaikan sistem persamaan berikut dengan metode Gauss:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 4x-4y+z=-4 \\[2ex] x+3y+z=2 \\[2ex] x+5y+2z=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b04370b42854e53c650ca0eae14aadb5_l3.png)
Hal pertama yang perlu kita lakukan adalah matriks yang diperluas dari sistem:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 4x-4y+z=-4 \\[2ex] x+3y+z=2 \\[2ex] x+5y+2z=6\end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 4 & -4 & 1 & -4 \\[2ex] 1 & 3 & 1 & 2 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff2c7644e19fdf405f3c5c42ffc0ee98_l3.png)
Untuk menerapkan metode Gauss, akan lebih mudah jika bilangan pertama pada baris pertama adalah 1. Oleh karena itu, kita akan mengubah urutan baris 1 dan 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 4 & -4 & 1 & -4 \\[2ex] 1 & 3 & 1 & 2 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 \rightarrow f_2} \\[2ex] \xrightarrow{f_2 \rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 4 & -4 & 1 & -4 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-471d89605d4bf6ddef1896a8fbe4c5ea_l3.png)
Sekarang kita perlu membuat semua angka di bawah array utama menjadi 0.
Oleh karena itu kami melakukan operasi baris untuk membatalkan dua suku terakhir dari kolom pertama:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 4 & -4 & 1 & -4 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 4f_1} \\[2ex] \xrightarrow{f_3 -f_1} \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 2 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f4d5cbc50b87927077018175c4678e90_l3.png)
Sekarang kita mengubah elemen terakhir kolom kedua menjadi nol:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 2 & 1 & 4 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{8f_3 + f_2} \end{array} \left( \begin{array}{ccc|c}1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 0 & 5 & 20 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-9013720883fd719e2bd0779bfbaa7a9f_l3.png)
Sistem ini adalah SCD , karena kami berhasil menggeser matriks dan baris terakhir bertipe
![]()
. Oleh karena itu, pihaknya akan memiliki solusi unik.
Setelah semua bilangan di bawah diagonal utama adalah 0, sekarang kita dapat menyelesaikan sistem persamaannya. Untuk melakukan ini, kita nyatakan kembali matriks tersebut dalam bentuk sistem persamaan dengan yang tidak diketahui:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 0 & 5 & 20 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+3y+1z=2 \\[2ex] -16y-3z=-12 \\[2ex] 5z=20 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0f0433738d5d0a22bdd3b04dbd44fd1e_l3.png)
Dan kami memecahkan persamaan yang tidak diketahui dari bawah ke atas. Pertama-tama kita selesaikan persamaan terakhir:
![]()
![]()
Sekarang kita substitusikan nilai z ke dalam persamaan kedua untuk mencari nilai y:
![]()
![]()
![]()
![]()
![]()
Dan kita melakukan hal yang sama dengan persamaan pertama: kita mengganti nilai-nilai yang tidak diketahui lainnya dan menyelesaikan x:
![]()
![]()
![]()
![]()
Oleh karena itu, penyelesaian sistem persamaan tersebut adalah:
![]()
Latihan 4
Tentukan jenis sistemnya dan selesaikan sistem persamaan berikut dengan metode Gauss:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-y+4z=2 \\[2ex] -3x-3y+3z=7 \\[2ex] -2x-4y+7z=9 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e8a133547b4719d7833a792550fd322_l3.png)
Hal pertama yang perlu kita lakukan adalah matriks yang diperluas dari sistem:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-y+4z=2 \\[2ex] -3x-3y+3z=7 \\[2ex] -2x-4y+7z=9 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c}1 & -1 & 4 & 2 \\[2ex] -3 & -3 & 3 & 7 \\[2ex] -2 & -4 & 7 & 9\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-cc41f78456a922a0fbff419d336b0b46_l3.png)
Sekarang kita perlu membuat semua angka di bawah array utama menjadi 0.
Oleh karena itu kami melakukan operasi baris untuk membatalkan dua suku terakhir dari kolom pertama:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] -3 & -3 & 3 & 7 \\[2ex] -2 & -4 & 7 & 9\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 3f_1} \\[2ex] \xrightarrow{f_3 + 2f_1} \end{array} \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & -6 & 15 & 13\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff92912f653c6aca7ceb7c990c9635a3_l3.png)
Sekarang mari kita coba menghapus elemen terakhir dari kolom kedua:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & -6 & 15 & 13\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -1f_2} \end{array} \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3c6904a64a721f3a92bef8c6b7d713cf_l3.png)
Tapi kita mendapatkan seluruh baris 0. Jadi ini adalah SCI dan sistemnya memiliki banyak sekali solusi.
Tapi karena ini adalah ICS, kita bisa menyelesaikan sistemnya berdasarkan
![]()
. Oleh karena itu kami menghapus baris 0:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6d856e2c1246f3629d68a7bcd3cd759a_l3.png)
Sekarang kita nyatakan matriks tersebut dalam bentuk sistem persamaan yang tidak diketahui:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x-1y+4z=2 \\[2ex] -6y+15z=13 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a4cf1265bfc12f94580de183230c8b7c_l3.png)
Kami memberi nilai
![]()
Untuk
![]()
![]()
Kami mengganti nilai
![]()
dalam persamaan kedua untuk mencari nilai
![]()
![]()
![]()
![]()
![]()
Dan kita melakukan hal yang sama dengan persamaan pertama: kita mengganti nilai-nilai yang tidak diketahui lainnya dan menghapusnya
![]()
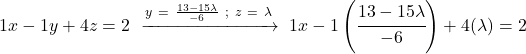
![]()
![]()
Kami memiliki jumlah dengan pecahan. Oleh karena itu, kami mereduksi semua suku menjadi penyebut yang sama:
![]()
![]()
Karena sekarang semuanya mempunyai penyebut yang sama, kita dapat mengelompokkannya menjadi satu pecahan:
![]()
Dan akhirnya kami mengoperasikan pembilangnya:
![]()
![]()
Oleh karena itu, penyelesaian sistem persamaan tersebut adalah:
![]()