Pembahasan sistem persamaan dengan parameter -

Pada halaman ini kita akan melihat bagaimana membahas dan menyelesaikan sistem persamaan dengan parameter . Selain itu, Anda akan menemukan contoh dan latihan penyelesaian sistem persamaan linear untuk dipraktikkan.

Di sisi lain, untuk menganalisis sistem persamaan linier, penting bagi Anda untuk mengetahui apa itu aturan Cramer dan apa itu teorema Rouché–Frobenius , karena kita akan menggunakannya terus-menerus.

Contoh sistem persamaan linear dengan parameter

Diskusikan dan selesaikan sistem persamaan berikut dengan parameter m :

$\begin{cases} x+y+2z= 2 \\[1.5ex] -x+my+2z=0 \\[1.5ex] 3x+mz = 4\end{cases}$

Pertama-tama kita buat matriks A dan matriks perluasan A’ dari sistem:

$\displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & m & 2 & 0 \\[1.1ex] 3 & 0 & m & 4 \end{array} \right)$

Sekarang kita selesaikan determinan A menggunakan aturan Sarrus, untuk melihat berapa rank matriksnya:

$\displaystyle\begin{aligned} \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{vmatrix} & =m^2+6+0-6m-0+m \\ & = m^2-5m+6 \end{aligned}$

Jadi hasil determinan A bergantung pada nilai m . Oleh karena itu, kita akan melihat nilai m mana yang determinannya hilang. Untuk melakukan ini, kami menetapkan hasilnya sama dengan 0 :

$\displaystyle m^2-5m+6 = 0$

Dan kita selesaikan persamaan kuadrat tersebut dengan rumus:

$\displaystyle m = \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$\displaystyle m = \cfrac{-(-5) \pm \sqrt{(-5)^2-4\cdot 1 \cdot 6}}{2 \cdot 1} = \cfrac{5 \pm \sqrt{25-24}}{2} =\cfrac{5 \pm 1}{2} = \begin{cases} \bm{m = 3} \\[2ex] \bm{m =2} \end{cases}$

Jadi jika m sama dengan 2 atau 3 maka determinan A akan sama dengan 0. Dan jika m berbeda dengan 2 dan berbeda dengan 3 maka determinan A akan berbeda dengan 0.

Oleh karena itu kita harus menganalisis setiap kasus secara terpisah:

m≠3 dan m≠2:

Seperti yang baru saja kita lihat, jika parameter m berbeda dengan 2 dan 3, determinan matriks A berbeda dengan 0. Oleh karena itu, rank A adalah 3 .

$\displaystyle rg(A)=3$

Selain itu, rank matriks A’ juga 3 , karena di dalamnya terdapat submatriks 3×3 yang determinannya berbeda dengan 0. Dan tidak mungkin berpangkat 4 karena ‘kita tidak dapat membuat determinan 4×4.

$\displaystyle rg(A')=3$

Kemudian, karena pangkat dari matriks A sama dengan pangkat dari matriks A’ dan dengan banyaknya sistem yang tidak diketahui (3), berdasarkan teorema Rouché-Frobenius kita mengetahui bahwa matriks tersebut adalah Depended System Kompatibel (SCD) :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

Setelah kita mengetahui bahwa sistem tersebut adalah Sistem yang Ditentukan Kompatibel (DCS), kita menerapkan aturan Cramer untuk menyelesaikannya. Untuk melakukannya, ingatlah bahwa matriks A, determinannya, dan matriks A’ adalah:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{vmatrix} = m^2-5m+6$

Untuk menghitung x dengan aturan Cramer, kita ubah kolom pertama determinan matriks A menjadi kolom suku bebas dan membaginya dengan determinan A:

$\displaystyle\bm{x} = \cfrac{\begin{vmatrix} 2 & 1 & 2\\[1.1ex]0&m&2 \\[1.1ex] 4 & 0 & m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{2m^2+8-8m}{m^2-5m+6}$

Untuk menghitung y dengan aturan Cramer, kita ubah kolom kedua determinan A menjadi kolom suku bebas dan membaginya dengan determinan A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 0 & 2 \\[1.1ex] 3 & 4 & m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}}=\cfrac{-4+2m}{m^2-5m+6}$

Untuk menghitung z dengan aturan Cramer, kita ubah kolom ketiga determinan A menjadi kolom suku bebas dan membaginya dengan determinan A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 0 \\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-2m+4}{m^2-5m+6}$

Oleh karena itu, penyelesaian sistem persamaan untuk kasus m≠3 dan m≠2 adalah:

$\displaystyle \bm{x =} \cfrac{\bm{2m^2+8-8m}}{\bm{m^2-5m+6}} \qquad \bm{y=} \cfrac{\bm{-4+2m}}{\bm{m^2-5m+6}} \qquad \bm{z =} \cfrac{\bm{-2m+4}}{\bm{m^2-5m+6}}$

Seperti yang Anda lihat, dalam hal ini solusi sistem persamaan adalah fungsi dari m.

Setelah kita menemukan solusi ketika m berbeda dari 2 dan 3, kita akan menyelesaikan sistem ketika m sama dengan 2:

m=2:

Sekarang kita akan menganalisis sistem jika parameter m sama dengan 2. Dalam hal ini matriks A dan A’ adalah:

$\displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & 2 & 2 \\[1.1ex] 3 & 0 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & 2 & 2 & 0 \\[1.1ex] 3 & 0 & 2 & 4 \end{array} \right)$

Seperti yang kita lihat sebelumnya, ketika m=2 determinan A adalah 0. Oleh karena itu, matriks A tidak berpangkat 3. Namun di dalamnya terdapat 2×2 determinan selain 0, misalnya:

$\displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 2 \end{vmatrix} = 2 - (-1)=3 \neq 0$

Jadi, dalam hal ini pangkat A adalah 2 :

$\displaystyle rg(A)=2$

Setelah kita mengetahui rank matriks A, kita menghitung rank A’. Penentu dari 3 kolom pertama menghasilkan 0, jadi kita coba kemungkinan determinan 3×3 lainnya pada matriks A’:

$\displaystyle \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] 2 & 2 & 0 \\[1.1ex] 0 & 2 & 4 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] -1 & 2 & 0 \\[1.1ex] 3 & 2 & 4 \end{vmatrix}=0\qquad \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & 2 & 0 \\[1.1ex] 3 & 0 & 4\end{vmatrix}=0$

Semua determinan yang mungkin untuk dimensi 3×3 menghasilkan 0. Namun, jelas bahwa matriks A’ mempunyai determinan non-0 2×2 yang sama dengan matriks A:

$\displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 2 \end{vmatrix} = 2 - (-1)=3 \neq 0$

Oleh karena itu, matriks A’ juga mempunyai rangking 2 :

$\displaystyle rg(A')=2$

Jadi, karena pangkat matriks A sama dengan pangkat matriks A’ tetapi keduanya lebih kecil dari jumlah sistem yang tidak diketahui (3), kita mengetahui melalui teorema Rouché-Frobenius bahwa ini adalah Sistem yang Kompatibel Tak Pasti (ICS):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

Karena ini adalah ICS, kita perlu mengubah sistem untuk mengatasinya. Untuk melakukan ini, pertama-tama kita harus menghilangkan persamaan dari sistem, dalam hal ini kita akan menghapus persamaan terakhir:

$\begin{cases} x+y+2z= 2 \\[1.5ex] -x+2y+2z=0 \\[1.5ex] \cancel{3x+2z = 4} \end{cases} \longrightarrow \quad \begin{cases} x+y+2z= 2 \\[1.5ex] -x+2y+2z=0\end{cases}$

Sekarang mari kita ubah variabel z menjadi λ:

$\begin{cases}x+y+2z= 2 \\[1.5ex] -x+2y+2z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+y+2\lambda= 2 \\[1.5ex] -x+2y+2\lambda=0\end{cases}$

Dan kami menempatkan suku dengan λ dengan suku independen:

$\begin{cases}x+y=2-2\lambda \\[1.5ex] -x+2y=-2\lambda \end{cases}$

Oleh karena itu, matriks A dan matriks A’ dari sistem tersebut tetap:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 1 \\[1.1ex] -1 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 1 & 2 -2\lambda \\[1.1ex] -1 & 2 & -2\lambda \end{array} \right)$

Terakhir, setelah kita mengubah sistem, kita menerapkan aturan Cramer . Untuk melakukan ini, pertama-tama kita selesaikan determinan A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 \\[1.1ex] -1 & 2\end{vmatrix} =2-(-1)=3$

Untuk menghitung x dengan aturan Cramer, kita ubah kolom pertama determinan A menjadi kolom suku bebas dan membaginya dengan determinan A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 -2\lambda & 1 \\[1.1ex] -2\lambda & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{4-4\lambda-(-2\lambda)}{3} = \cfrac{\bm{4-2\lambda}}{\bm{3}}$

Untuk menghitung y dengan aturan Cramer, kita ubah kolom kedua determinan A menjadi kolom suku bebas dan membaginya dengan determinan A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 2 -2\lambda \\[1.1ex] -1 & -2\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}}=\cfrac{-2\lambda -(-2+2\lambda)}{3} = \cfrac{\bm{2-4\lambda} }{\bm{3}}$

Sehingga ketika m=2 solusi sistem persamaan tersebut adalah fungsi dari λ, karena merupakan SCI dan oleh karena itu memiliki solusi tak terhingga:

$\displaystyle \bm{x =} \cfrac{\bm{4-2\lambda}}{\bm{3}} \qquad \bm{y=}\cfrac{\bm{2-4\lambda}}{\bm{3}} \qquad \bm{z=\lambda}$

Kita telah menganalisis solusi sistem ketika parameter m berbeda dari 2 dan 3, dan ketika sama dengan 2. Oleh karena itu, kita hanya memerlukan kasus terakhir: ketika m bernilai 3:

m=3:

Sekarang kita akan menganalisis apa yang terjadi jika parameter m adalah 3. Dalam hal ini matriks A dan A’ adalah:

$\displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & 3 & 2 \\[1.1ex] 3 & 0 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & 3 & 2 & 0 \\[1.1ex] 3 & 0 & 3 & 4 \end{array} \right)$

Seperti yang kita lihat sebelumnya, ketika m=3 determinan A adalah 0. Jadi matriks A tidak berpangkat 3. Namun di dalamnya terdapat 2×2 determinan yang berbeda dengan 0, misalnya:

$\displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 3 \end{vmatrix} = 3 - (-1)=4 \neq 0$

Jadi, dalam hal ini pangkat A adalah 2 :

$\displaystyle rg(A)=2$

Setelah kita mengetahui rank matriks A, kita menghitung rank A’. Penentu 3 kolom pertama menghasilkan 0, oleh karena itu kita coba determinan 3×3 lain yang ada di dalam matriks A’, misalnya matriks 3 kolom terakhir:

$\displaystyle \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] 3 & 2 & 0 \\[1.1ex] 0 & 3 & 4\end{vmatrix}=2$

Sebaliknya matriks A’ memang mengandung determinan yang hasilnya berbeda dengan 0, sehingga matriks A’ mempunyai rank 3 :

$\displaystyle rg(A')=3$

Jadi, ketika m = 3, pangkat matriks A lebih rendah daripada pangkat matriks A’. Jadi, dari teorema Rouché-Frobenius, kami menyimpulkan bahwa sistem tersebut adalah Sistem yang Tidak Kompatibel (IS) :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas}=3\end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A)=2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

Oleh karena itu, sistem persamaan tidak memiliki solusi jika m = 3.

Ringkasan contoh:

Seperti yang telah kita lihat, penyelesaian sistem persamaan bergantung pada nilai parameter m . Berikut adalah ringkasan dari semua kemungkinan kasus:

m≠3 dan m≠2:

$\displaystyle \bm{SCD} \longrightarrow \begin{cases} x = \cfrac{2m^2+8-8m}{m^2-5m+6} \\[3.5ex] y =\cfrac{-4+2m}{m^2-5m+6} \\[3.5ex] z = \cfrac{-2m+4}{m^2-5m+6} \end{cases}$

m=2:

$\displaystyle \bm{SCI} \longrightarrow \begin{cases} x = \cfrac{4-2\lambda}{3} \\[3.5ex] y= \cfrac{2-4\lambda}{3} \\[3.5ex] z = \lambda \end{cases}$

m=3:

$\displaystyle \bm{SI} \longrightarrow$

Sistem tidak memiliki solusi.

Di sini kita telah melakukan seluruh proses menggunakan teorema Rouche dan aturan Cramer, namun sistem persamaan dengan parameter juga dapat didiskusikan dan diselesaikan denganmetode Gauss (dengan latihan) . Anda dapat mempelajari lebih lanjut tentang metode ini di halaman tertaut, di mana Anda akan menemukan penjelasan rinci tentang prosedur serta contoh dan latihan yang diselesaikan langkah demi langkah.

Pembahasan Soal Pembahasan Sistem Persamaan Linier dengan Parameter

Latihan 1

Diskusikan dan selesaikan sistem persamaan linier bergantung parameter berikut:

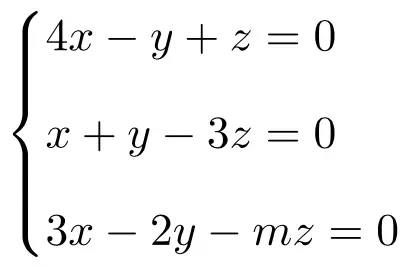
menyelesaikan latihan sistem persamaan dengan parameter

lihat solusi

Pertama-tama kita buat matriks A dan matriks perluasan A’ dari sistem:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & -m & 0\end{array} \right)$

Sekarang kita harus mencari rank matriks A. Untuk melakukannya, kita periksa apakah determinan seluruh matriks berbeda dari 0:

$\displaystyle \begin{aligned}\begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{vmatrix} & =-4m+9-2-3-24-m \\ & =-5m-20 \end{aligned}$

Hasil determinan A bergantung pada nilai m. Oleh karena itu, kita akan melihat nilai m mana yang determinannya hilang. Untuk melakukan ini, kita menyamakan hasil yang dihasilkan dengan 0 dan menyelesaikan persamaan:

$-5m-20 = 0$

$-5m = 20$

$m = \cfrac{20}{-5} = -4$

Jadi, ketika m adalah -4, determinan dari A adalah 0. Dan ketika m berbeda dari -4, determinan dari A akan berbeda dari 0. Oleh karena itu kita harus menganalisis setiap kasus secara terpisah:

m≠-4:

Seperti yang baru saja kita lihat, jika parameter m berbeda dari -4, maka determinan matriks A berbeda dari 0. Oleh karena itu, rank A adalah 3.

$\displaystyle rg(A)=3$

Selain itu, rank matriks A’ juga 3, karena di dalamnya terdapat submatriks 3×3 yang determinannya berbeda dengan 0. Dan tidak mungkin mempunyai rank 4 karena ‘kita tidak dapat membuat determinan 4×4.

$\displaystyle rg(A')=3$

Oleh karena itu, dengan menerapkan teorema Rouché-Frobenius, kita mengetahui bahwa ini adalah sistem determinasi yang kompatibel (SCD), karena jangkauan A sama dengan jangkauan A’ dan jumlah yang tidak diketahui.

Setelah kami mengetahui bahwa sistem tersebut adalah SCD, kami menerapkan aturan Cramer untuk menyelesaikannya. Untuk melakukannya, ingatlah bahwa matriks A, determinannya, dan matriks A’ adalah:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & -m & 0\end{array} \right)$

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m\end{vmatrix} =-5m-20$

Untuk menghitung xatex] dengan aturan Cramer, kita ubah kolom pertama determinan A dengan kolom suku bebas dan membaginya dengan determinan A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 0 & -1 & 1 \\[1.1ex] 0 & 1 & -3 \\[1.1ex] 0 & -2 & -m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}$

Untuk menghitung yang tidak diketahui dan dengan aturan Cramer, kita ubah kolom kedua determinan A dengan kolom suku bebas dan kita bagi dengan determinan A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 4 & 0 & 1 \\[1.1ex] 1 & 0 & -3 \\[1.1ex] 3 & 0 & -m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}$

Untuk menghitung z dengan aturan Cramer, kita ubah kolom ketiga determinan A menjadi kolom suku bebas dan membaginya dengan determinan A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix}4 & -1 & 0 \\[1.1ex] 1 & 1 & 0 \\[1.1ex] 3 & -2 & 0 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}$

Oleh karena itu, penyelesaian sistem persamaan untuk kasus m≠-4 adalah:

x=0 kamu=0 z=0

m=-4:

Kami sekarang akan menganalisis sistem ketika parameter m adalah -4. Dalam hal ini matriks A dan A’ adalah:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & 4 & 0\end{array} \right)$

Seperti yang kita lihat sebelumnya, ketika m=-4 determinan A adalah 0. Jadi, matriks A tidak berpangkat 3. Namun di dalamnya terdapat 2×2 determinan selain 0, misalnya:

$\displaystyle \begin{vmatrix}4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} =4-(-1)=5 \neq 0$

Karena matriks mempunyai determinan orde 2 yang berbeda dengan 0, maka matriks A mempunyai rank 2:

$\displaystyle rg(A)=2$

Setelah kita mengetahui pangkat A, kita menghitung pangkat A’. Kita sudah tahu bahwa determinan dari 3 kolom pertama menghasilkan 0, jadi kita coba kemungkinan determinan 3×3 lainnya:

$\displaystyle \begin{vmatrix} -1 & 1 & 0 \\[1.1ex] 1 & -3 & 0 \\[1.1ex] -2 & 4 & 0 \end{vmatrix} = 0 \quad \begin{vmatrix}4 & 1 & 0 \\[1.1ex] 1 & -3 & 0 \\[1.1ex] 3 & 4 & 0 \end{vmatrix} = 0 \quad \begin{vmatrix}4 & -1 & 0 \\[1.1ex] 1 & 1 & 0 \\[1.1ex] 3 & -2 & 0\end{vmatrix} = 0$

Semua determinan matriks A’ berukuran 3×3 adalah 0, sehingga matriks A’ juga tidak menduduki rangking 3. Namun di dalamnya memang terdapat determinan orde 2 yang berbeda dengan 0. Contoh:

$\displaystyle \begin{vmatrix}4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} =4-(-1)=5 \neq 0$

Jadi matriks A’ akan mempunyai rangking 2:

$\displaystyle rg(A')=2$

Luas matriks A sama dengan luas matriks A’ tetapi keduanya lebih kecil dari jumlah yang tidak diketahui dalam sistem (3), oleh karena itu, menurut teorema Rouché-Frobenius, c adalah Sistem Kompatibel Tak tentu (ICS):

Ini adalah sistem ICS, jadi kita perlu mengubah sistem untuk menyelesaikannya. Pertama-tama kita hilangkan satu persamaan, yang dalam hal ini akan menjadi persamaan terakhir:

$\begin{cases} 4x-y+z= 0 \\[1.5ex] x+y-3z=0 \\[1.5ex] \cancel{3x-2y+4z = 0} \end{cases} \longrightarrow \quad \begin{cases} 4x-y+z= 0 \\[1.5ex] x+y-3z=0\end{cases}$

Sekarang mari kita ubah variabel z menjadi λ:

$\begin{cases}4x-y+z= 0 \\[1.5ex] x+y-3z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 4x-y+\lambda= 0 \\[1.5ex] x+y-3\lambda=0\end{cases}$

Dan kami menempatkan suku dengan λ dengan suku independen:

$\begin{cases} 4x-y=-\lambda \\[1.5ex] x+y=3\lambda \end{cases}$

Sehingga matriks A dan matriks A’ sistem tetap:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 \\[1.1ex] 1 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 4 & -1 & -\lambda \\[1.1ex] 1 & 1 & 3\lambda \end{array} \right)$

Terakhir, setelah kita mengubah sistem, kita menerapkan aturan Cramer. Untuk melakukan ini, pertama-tama kita selesaikan determinan A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} = 4-(-1)=5$

Untuk menghitung x dengan aturan Cramer, kita ubah kolom pertama determinan A menjadi kolom suku bebas dan membaginya dengan determinan A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix}-\lambda & -1 \\[1.1ex] 3\lambda & 1 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-\lambda-(-3\lambda)}{5} =\cfrac{\bm{2\lambda}}{\bm{5}}$

Untuk menghitung yang tidak diketahui dan dengan aturan Cramer, kita ubah kolom kedua determinan A dengan kolom suku bebas dan kita bagi dengan determinan A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 4 & -\lambda \\[1.1ex] 1 & 3\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12\lambda-(-\lambda)}{5}=\cfrac{\bm{13\lambda}}{\bm{5}}$

Sehingga ketika m=-4 solusi sistem persamaan tersebut adalah fungsi dari λ, karena merupakan SCI dan karenanya memiliki solusi tak terhingga:

$\displaystyle \bm{x =}\cfrac{\bm{2\lambda}}{\bm{5}}\qquad \bm{y=}\cfrac{\bm{13\lambda}}{\bm{5}} \qquad \bm{z=\lambda}$

Latihan 2

Diskusikan dan temukan solusi sistem persamaan linear bergantung parameter berikut:

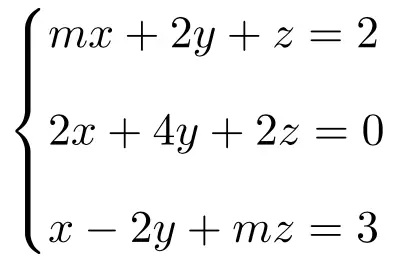
latihan diselesaikan langkah demi langkah sistem persamaan linear dengan parameter

lihat solusi

Hal pertama yang harus dilakukan adalah matriks A dan matriks perluasan A’ dari sistem:

$\displaystyle A= \left( \begin{array}{ccc} m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}m & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & m & 3\end{array} \right)$

Sekarang kita harus mencari rank matriks A. Untuk melakukannya, kita periksa apakah determinan seluruh matriks berbeda dari 0:

$\displaystyle \begin{aligned}\begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{vmatrix} & =4m^2+4-4-4+4m-4m \\ & =4m^2-4 \end{aligned}$

$4m^2-4 = 0$

$4m^2=4$

$m^2 = \cfrac{4}{4}$

$m^2 = 1$

$m = \pm 1$

Jadi, jika m adalah +1 atau -1, maka determinan dari A adalah 0. Dan jika m berbeda dari +1 dan -1, maka determinan A akan berbeda dari 0. Oleh karena itu kita harus menganalisis setiap kasus dengan:

m≠+1 dan m≠-1:

Seperti yang baru saja kita lihat, jika parameter m berbeda dari +1 dan -1, determinan matriks A berbeda dari 0. Oleh karena itu, rank A adalah 3.

$\displaystyle rg(A)=3$

$\displaystyle rg(A')=3$

Setelah kami mengetahui bahwa sistem tersebut adalah SCD, kami menerapkan aturan Cramer untuk menyelesaikannya. Untuk melakukannya, ingatlah bahwa matriks A, determinannya, dan matriks A’ adalah:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{vmatrix}=4m^2-4$

Untuk menghitung x dengan aturan Cramer, kita ubah kolom pertama determinan A menjadi kolom suku bebas dan membaginya dengan determinan A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2& 2 & 1 \\[1.1ex] 0 & 4 & 2 \\[1.1ex] 3 & -2 & m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{8m+8}}{\bm{4m^2-4}}$

Untuk menghitung yang tidak diketahui dan dengan aturan Cramer, kita ubah kolom kedua determinan A dengan kolom suku bebas dan kita bagi dengan determinan A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} m & 2 & 1 \\[1.1ex] 2 & 0 & 2 \\[1.1ex] 1 & 3 & m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{-10m+10}}{\bm{4m^2-4}}$

Untuk menghitung z dengan aturan Cramer, kita ubah kolom ketiga determinan A menjadi kolom suku bebas dan membaginya dengan determinan A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix}m & 2 & 2 \\[1.1ex] 2 & 4 & 0 \\[1.1ex] 1 & -2 & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{12m-28}}{\bm{4m^2-4}}$

Oleh karena itu, penyelesaian sistem persamaan untuk kasus m≠+1 dan m≠-1 adalah:

$\displaystyle \bm{x = }\cfrac{\bm{8m+8}}{\bm{4m^2-4}} \qquad \bm{y=}\cfrac{\bm{-10m+10}}{\bm{4m^2-4}}\qquad \bm{z =} \cfrac{\bm{12m-28}}{\bm{4m^2-4}}$

m=+1:

Sekarang kita akan menganalisis sistem jika parameter m sama dengan 1. Dalam hal ini matriks A dan A’ adalah:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}1 & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & 1 & 3\end{array} \right)$

Seperti yang kita lihat sebelumnya, ketika m=+1 determinan A adalah 0. Jadi matriks A tidak berpangkat 3. Namun di dalamnya terdapat 2×2 determinan selain 0, misalnya:

$\displaystyle \begin{vmatrix}2 & 4\\[1.1ex] 1 & -2 \end{vmatrix} =-4-4=-8 \neq 0$

Karena matriks mempunyai determinan orde 2 yang berbeda dengan 0, maka matriks A mempunyai rank 2:

$\displaystyle rg(A)=2$

Setelah kita mengetahui pangkat A, kita menghitung pangkat A’. Kita sudah tahu bahwa determinan dari 3 kolom pertama menghasilkan 0, jadi sekarang kita coba, misalnya, dengan determinan dari 3 kolom terakhir:

$\displaystyle \begin{vmatrix} 2 & 1 & 2 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -2 & 1 & 3 \end{vmatrix} = 16$

Sebaliknya matriks A’ memang mengandung determinan 3×3 yang hasilnya berbeda dengan 0, sehingga matriks A’ mempunyai rank 3:

$\displaystyle rg(A')=3$

Jadi, ketika m=+1 pangkat matriks A lebih kecil dari pangkat matriks A’. Jadi, dari teorema Rouché-Frobenius, kami menyimpulkan bahwa sistem tersebut adalah Sistem yang Tidak Kompatibel (IS):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

Oleh karena itu, sistem persamaan tidak memiliki solusi ketika m=+1 , karena merupakan sistem yang tidak kompatibel.

m=-1:

Sekarang kita akan menganalisis sistem ketika parameter m adalah -1. Dalam hal ini matriks A dan A’ adalah:

$\displaystyle A= \left( \begin{array}{ccc} -1 & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}-1 & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & -1 & 3\end{array} \right)$

Seperti yang kita lihat sebelumnya, ketika m=-1 determinan A adalah 0. Jadi, matriks A tidak berpangkat 3. Namun di dalamnya terdapat 2×2 determinan selain 0, misalnya:

$\displaystyle \begin{vmatrix}-1 & 2\\[1.1ex] 2 & 4 \end{vmatrix} =-4-4=-8 \neq 0$

Karena matriks mempunyai determinan orde 2 yang berbeda dengan 0, maka matriks A mempunyai rank 2:

$\displaystyle rg(A)=2$

$\displaystyle \begin{vmatrix} -1 & 1 & 2 \\[1.1ex] 2 & 2 & 0 \\[1.1ex] 1 & -1 & 3\end{vmatrix} = -20$

Sebaliknya matriks A’ memang mengandung determinan 3×3 yang hasilnya berbeda dengan 0, sehingga matriks A’ mempunyai rank 3:

$\displaystyle rg(A')=3$

Jadi, ketika m = -1, pangkat matriks A lebih rendah daripada pangkat matriks A’. Jadi, dari teorema Rouché-Frobenius, kami menyimpulkan bahwa sistem tersebut adalah Sistem yang Tidak Kompatibel (IS):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

Oleh karena itu, sistem persamaan tidak memiliki solusi ketika m=-1 , karena merupakan sistem yang tidak kompatibel.

Contoh sistem persamaan linear dengan parameter

Ringkasan contoh:

Pembahasan Soal Pembahasan Sistem Persamaan Linier dengan Parameter

Latihan 1

Latihan 2

Tinggalkan Komentar Batalkan Balasan