Pecahan atau bilangan campuran adalah ekspresi numerik yang menunjukkan suatu besaran dibagi dengan besaran lain. Oleh karena itu, ini adalah nilai yang diwakili oleh hasil bagi dua angka. Dengan jenis bilangan ini kita dapat menyatakan besaran desimal dan bilangan bulat dan bahkan kita dapat menunjukkan proporsinya . Selanjutnya, kami akan mendefinisikan pecahan secara lebih matematis dan menunjukkan beberapa contoh, sehingga Anda dapat memahami konsep ini secara grafis.
Apa itu pecahan?
Pecahan sama dengan banyaknya bagian yang kita ambil dari suatu satuan yang dibagi menjadi bagian-bagian yang sama. Jadi secara grafis diwakili oleh dua suku yang dipisahkan oleh garis horizontal di tengahnya. Lebih tepatnya, di bagian atas garis kita temukan pembilangnya dan di bawah penyebutnya.
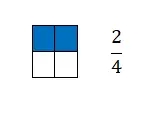
Seperti yang Anda lihat, pecahan adalah konsep matematika yang sangat mudah untuk dibuat grafiknya karena pecahan sejalan dengan proporsi. Inilah sebabnya pada contoh sebelumnya kita menyatakan banyaknya kotak berwarna dengan bilangan pecahan.
Istilah pecahan
Dua bagian pecahan adalah:
- Pembilang : Suku ini letaknya diatas garis mendatar dan disinilah kita menuliskan banyaknya keping yang kita ambil. Kita dapat mencari pembilang positif, negatif, dan nol (sama dengan nol).
- Penyebut: Suku lain ini terletak di bawah garis dan di sinilah kita menulis jumlah bagian yang membagi satuan tersebut. Kita bisa mencari penyebut positif dan negatif, tapi penyebutnya tidak boleh nol.
jenis pecahan
Pecahan ada banyak macamnya, tergantung pada bilangan penyusunnya dan persamaannya dengan pecahan lain. Selanjutnya kita akan mendefinisikan semua kategori yang ada dan kita akan mengomentari ciri-ciri yang memungkinkannya dibedakan dari yang lain:
- Pecahan wajar: adalah pecahan yang pembilangnya lebih kecil dari penyebutnya. Jika Anda mengubah pecahan ini menjadi desimal , Anda akan mendapatkan angka antara nol dan satu. Tidak boleh lebih besar dari satu, karena nilai pembilangnya akan selalu lebih kecil dari nilai penyebutnya sehingga kesatuan tidak akan terlampaui.
- Pecahan tak wajar: adalah pecahan yang pembilangnya lebih besar dari penyebutnya, dalam hal ini menyatakan nilai numerik lebih besar dari satu. Misalnya, 8/5 sama dengan 1,6 yang lebih besar dari 1. Ini adalah cara lain untuk menyatakan bilangan campuran, yaitu tipe berikut.
- Pecahan campuran: disebut juga bilangan campuran, adalah pecahan yang terdiri dari bilangan bulat dan bilangan campuran. Pada dasarnya bilangan tersebut direpresentasikan dengan nilai bilangan bulat sebelum pecahan, jadi untuk mengubahnya menjadi pecahan biasa, Anda perlu mengalikan bagian bilangan bulat dengan penyebutnya, menambahkannya ke pembilangnya, dan membiarkan penyebutnya tetap sama.
- Pecahan desimal: adalah pecahan yang penyebutnya menyatakan besaran yang setara dengan pangkat sepuluh, misalnya: 6/10, 34/1000, atau 5/100. Ini digunakan dalam notasi desimal dan paling umum saat mengonversi bilangan desimal eksak menjadi bilangan campuran. Kami akan membahas ini lebih detail di bagian berikutnya.
- Pecahan majemuk: adalah pecahan yang tersusun dari pecahan lain, baik yang pembilangnya, penyebutnya, atau kedua-duanya. Jadi untuk menyederhanakan persamaan ini dan menampilkannya sebagai pecahan tunggal, kita perlu membagi pembilangnya dengan penyebutnya. Hal ini akan menjadi lebih jelas setelah kita menjelaskan pembagian antar pecahan.
- Pecahan senilai: adalah pecahan yang mempunyai bilangan sama, meskipun pembilang dan penyebutnya tidak sama. Misalnya 8/4 = 4/2 = 2, kedua pecahan sama dengan dua. Dalam kasus khusus ini, karena pecahan pertama sama dengan dua kali pecahan kedua, sehingga mempertahankan hubungan proporsional.
- Pecahan tak tersederhanakan: Pecahan yang tidak dapat disederhanakan lagi karena pembilang dan penyebutnya tidak memiliki faktor persekutuan sehingga tidak dapat dibagi dengan bilangan apa pun. Beberapa contoh tipe ini antara lain: 9/5, 5/6, 7/8. Untuk mengetahui cara mendeteksinya, penting untuk mengetahui cara menghitung pembagi persekutuan terbesar .
Operasi dengan pecahan
Sekarang setelah kita mengetahui berbagai kategori pecahan yang ada, kita akan melihat cara menyelesaikan berbagai operasi aritmatika dengan bilangan campuran . Perlu dicatat bahwa ini sedikit lebih rumit daripada operasi dengan bilangan bulat, meskipun setelah Anda memahami metodologinya, semuanya menjadi cukup mudah. Selain itu, kami tidak hanya akan menjelaskan teorinya saja, tetapi kami juga akan menunjukkan beberapa contohnya. Karena itu, mari kita mulai.
jumlah pecahan
Menjumlahkan pecahan dengan penyebut yang sama cukup mudah, karena Anda cukup menjumlahkan kedua pembilangnya dan membiarkan penyebutnya tetap sama. Sebaliknya, menjumlahkan pecahan yang penyebutnya berbeda akan sedikit rumit karena Anda harus mencari kelipatan persekutuan terkecil dari penyebutnya. Selanjutnya kita harus menjumlahkan hasil kali masing-masing pembilangnya dengan membagi lcm (penyebut baru) dengan penyebut yang lama. Untuk lebih memahaminya, Anda dapat melihat diagram berikut:
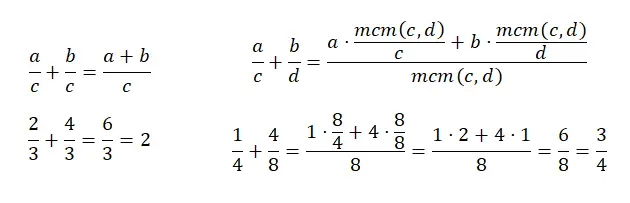
pecahan pengurangan
Pengurangan pecahan dengan penyebut yang sama sangat mirip dengan penjumlahan, sebenarnya semuanya dilakukan dengan cara yang sama kecuali pada penjumlahan pembilangnya, karena alih-alih menjumlahkan, Anda harus mengurangi. Dan pada pengurangan pecahan yang penyebutnya berbeda, hal yang sama terjadi, pada dasarnya sama, hanya saja alih-alih menjumlahkan hasil kali pembilangnya dengan membagi lcm dengan penyebut yang lama, kita harus mengurangi . Berikut diagram lainnya:
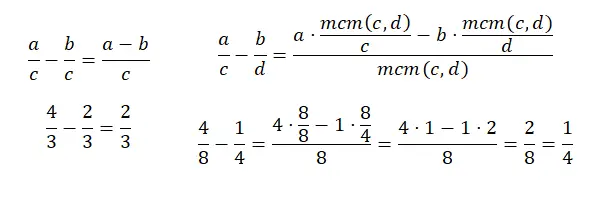
perkalian pecahan
Mengalikan pecahan dapat diselesaikan dengan cara yang sama, baik penyebutnya sama atau tidak. Pada dasarnya, Anda harus mengalikan pembilangnya dengan satu bagian dan penyebutnya dengan bagian lainnya. Ini mungkin operasi paling sederhana karena Anda hanya perlu melakukan dua perkalian.
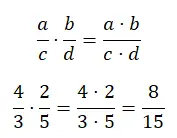
pembagian pecahan
Pembagian menjadi pecahan juga cukup mudah untuk diselesaikan, Anda hanya perlu mengalikan tanda silangnya. Dengan kata lain, pembilangnya adalah hasil perkalian pembilang pecahan pertama dengan penyebut pecahan kedua. sedangkan penyebutnya adalah hasil kali penyebut pecahan pertama dan pembilang pecahan kedua.
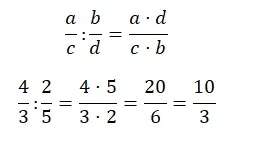
Sederhanakan pecahan
Menyederhanakan pecahan atau mengurangi pecahan bukanlah operasi aritmatika , tetapi sangat penting untuk mengetahui cara melakukannya dan juga merupakan topik yang telah kita bahas sedikit tentang jenis-jenis pecahan. Jadi, untuk menyederhanakan bilangan campuran, kita perlu membagi pembilang dan penyebutnya dengan bilangan yang sama. Umumnya, kita akan memilih faktor persekutuan terbesar untuk melakukan penyederhanaan ini. Pada gambar berikut Anda dapat menemukan contohnya.
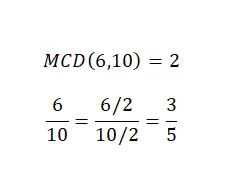
Seperti yang bisa Anda lihat, kita punya dua pecahan senilai , sehingga keduanya mewakili nilai numerik yang sama, namun pecahan kedua lebih sederhana daripada pecahan pertama. Oleh karena itu, kami telah berhasil mencapai tujuan penyederhanaan.
Bagaimana cara mengubah desimal ke pecahan dan sebaliknya?
Pecahan pembangkit adalah pecahan tak tersederhanakan yang diperoleh dari suatu bilangan desimal, baik bilangan desimal eksak maupun bilangan desimal berulang. Tentu saja, kita perlu menggunakan metode yang berbeda tergantung pada jenis desimalnya, yang akan kita bahas di bawah.
Konversi dari desimal eksak menjadi pecahan yang menghasilkan
Dalam hal ini kita dapat menggunakan pecahan desimal yang telah kita komentari di awal. Sederhananya, kita perlu menuliskan nilai numerik pada pembilangnya, tetapi tanpa koma. Sedangkan pada penyebutnya kita tuliskan pangkat sepuluh yang angka nolnya sama banyaknya dengan angka pada pembilangnya.
Namun, jika kita mempunyai bilangan desimal yang lebih besar dari satu, misalnya 4,25, maka kita perlu mengalikan banyaknya satuan lengkap yang kita miliki dengan nilai penyebutnya dan menjumlahkannya dengan pembilang aslinya. Di bawah ini Anda akan menemukan contoh masing-masing jenis:
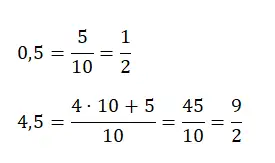
Ubah desimal berulang murni menjadi pecahan yang menghasilkan
Jika kita memiliki bilangan desimal periodik murni , jika kita ingin mendapatkan pecahan yang menghasilkan, kita harus memasukkan nilai yang sama pada pembilangnya, tetapi tanpa koma dan mengurangkan bagian bilangan bulatnya. Meskipun penyebutnya sama dengan bilangan yang hanya terdiri dari sembilan, kita harus menuliskan secara spesifik bilangan sembilan sebanyak jumlah digit di bagian desimal bilangan aslinya. Sistem ini agak membingungkan, tetapi dengan beberapa contoh, kita akan memahami:
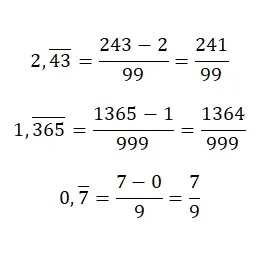
Ubah desimal berulang campuran menjadi pecahan yang dihasilkan
Jika terdapat bilangan desimal campuran yang berulang , kita harus menerapkan aturan yang cukup rumit. Pertama, kita akan menuliskan bilangan tanpa koma pada pembilangnya dan mengurangkan bagian bilangan bulat diikuti dengan desimal tidak berulang, juga tanpa koma. Sedangkan untuk penyebutnya, Anda perlu menuliskan angka sembilan sebanyak jumlah digit pada bagian desimal periodik, diikuti dengan angka nol sebanyak jumlah angka pada bagian desimal tidak berulang.
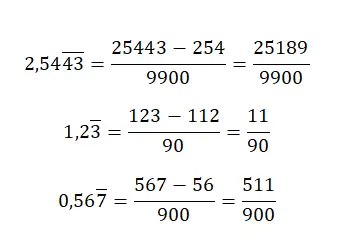
mengubah pecahan menjadi desimal
Untuk beralih dari pecahan ke desimal, cukup bagi pembilangnya dengan penyebutnya, karena bilangan campuran tidak lebih dari hasil bagi antara dua nilai . Jadi, dengan menyelesaikan pembagian, Anda mendapatkan bilangan desimal yang sesuai. Pada gambar berikut Anda dapat menemukan beberapa contoh yang cukup sederhana:
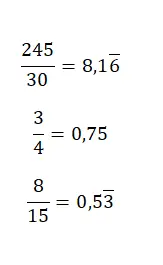
latihan pecahan
Sekarang setelah Anda mengetahui semua teori tentang pecahan, kami menyarankan Anda melakukan beberapa latihan. Dengan cara ini Anda akan mempelajari semua konsep yang dijelaskan secara lebih mendalam dan pada hari ujian Anda akan lebih cepat dalam menyelesaikan perhitungan. Selain itu, Anda akan melihat semua jenis latihan pecahan yang ada dan Anda akan mengetahui cara menyelesaikannya dengan tepat. Terakhir, izinkan saya memberi tahu Anda bahwa kami juga memiliki kalkulator pecahan online yang dapat Anda gunakan untuk menyelesaikan semua operasi pecahan.