Pada artikel ini kami menjelaskan operasi apa saja yang dapat dilakukan dengan fungsi. Anda akan dapat melihat penjelasan serta latihan penyelesaian operasi dengan fungsi. Dan terakhir, Anda akan menemukan properti operasi dengan fungsi.
Apa yang dimaksud dengan operasi dengan fungsi?
Anda dapat melakukan 5 jenis operasi berbeda dengan fungsi: penjumlahan, pengurangan, perkalian, pembagian, dan komposisi. Artinya, dua fungsi dapat dijumlahkan, dikurangi, dikalikan, dibagi, atau dikomposisi.
Selanjutnya kita akan melihat bagaimana setiap jenis operasi dilakukan beserta fungsi dan karakteristiknya masing-masing.
Jumlah fungsi
Nilai penjumlahan (atau penjumlahan) dua fungsi sama dengan jumlah nilai masing-masing fungsi. Dengan kata lain, untuk menghitung citra suatu fungsi penjumlahan, cukup tambahkan citra fungsi-fungsi yang terlibat dalam operasi tersebut.
![]()
Selanjutnya, daerah asal penjumlahan dua fungsi merupakan perpotongan daerah asal setiap fungsi yang dijumlahkan.
![]()
Mari kita lihat bagaimana dua fungsi ditambahkan menggunakan sebuah contoh:
![]()
Kami pertama-tama menambahkan dua fungsi:
![]()
Dan sekarang kita menemukan domain dari fungsi penjumlahan. Untuk melakukan ini, kami menghitung domain setiap fungsi secara terpisah:
![]()
➤ Lihat: cara menghitung domain suatu fungsi
Maka domain dari fungsi yang dihasilkan dari operasi tersebut adalah:
![]()
Setiap operasi dengan fungsi harus disertai dengan domainnya untuk menentukan hasilnya secara lengkap.
Pengurangan fungsi
Bayangan pengurangan (atau selisih) dua fungsi adalah pengurangan bayangan setiap fungsi yang ikut serta dalam operasi:
![]()
Seperti halnya fungsi penjumlahan, domain pengurangan dua fungsi ekuivalen dengan perpotongan domain masing-masing fungsi.
![]()
Jadi, jika suatu fungsi tidak terdefinisi pada nilai tertentu dari variabel bebas x, maka fungsi hasil pengurangan juga tidak akan terdefinisi.
Mari kita lihat bagaimana dua fungsi dikurangi melalui sebuah contoh:
![]()
Pertama-tama kita kurangi kedua fungsi tersebut:
![]()
Dan kemudian kita menentukan domain dari fungsi pengurangan:
![]()
![]()
Produk andalan
Untuk menghitung hasil kali atau (perkalian) dua fungsi , Anda cukup mengalikan ekspresi masing-masing fungsi.
![]()
Di sisi lain, domain dari fungsi hasil kali adalah himpunan perpotongan domain dari setiap fungsi yang dikalikan.
![]()
Misalnya, jika kita mempunyai dua fungsi berikut:
![]()
Pertama, kami menjalankan pengoperasian produk dengan dua fungsi:
![]()
Dan terakhir, kita mencari domain dari fungsi yang dihasilkan dari operasi tersebut:
![]()
![]()
Distribusi fungsi
Hasil numerik dari pembagian (atau hasil bagi) dua fungsi sesuai dengan persamaan berikut:
![]()
Namun domain pembagian dua fungsi adalah himpunan perpotongan domain masing-masing fungsi dikurangi semua x yang menghilangkan fungsi yang berperan sebagai pembagi, karena jika tidak maka akan diperoleh ketidakpastian.
![]()
Sebagai contoh, kita akan membagi fungsi-fungsi berikut:
![]()
Pembagian fungsinya adalah sebagai berikut:
![]()
Sebaliknya, domain setiap fungsi secara terpisah terdiri dari semua bilangan real
![]()
Namun, karena penyebut suatu pecahan tidak boleh ada nol, maka dalam domain fungsi yang dihasilkan kita harus menghilangkan semua nilai yang menghilangkan penyebutnya (x=3).
![]()
Komposisi fungsi
Komposisi fungsi merupakan operasi yang paling sulit diselesaikan, karena merupakan konsep yang paling rumit.
Komposisi fungsi terdiri dari penerapan dua fungsi secara berurutan. Secara aljabar, komposisi dua fungsi tersebut dinyatakan sebagai berikut:
![]()
Di sisi lain, domain komposisi fungsi
![]()
ekuivalen dengan himpunan semua nilai x pada domain fungsi
![]()
seperti
![]()
termasuk dalam domain fungsi
![]()
![]()
Misalnya, diberikan dua fungsi berikut:
![]()
Untuk mencari fungsi gabungan
![]()
diikuti oleh
![]()
kita perlu mengganti ekspresi
![]()
dimana ada satu
![]()
dalam ekspresi
![]()
![Rendered by QuickLaTeX.com \begin{aligned}(g\circ f)(x)&=g\Bigl(f(x)\Bigr)\\[2ex]&= g\Bigl(x^2+1\Bigr)\\[2ex]&=3(x^2+1)-4\\[2ex]&=3x^2+3-4\\[2ex]&=3x^2-1\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f48079d61cf80409fdbf6610b5724189_l3.png)
Dalam hal ini domain kedua fungsi tersebut seluruhnya terdiri dari bilangan real, sehingga domain dari fungsi komposit tersebut juga akan terdiri dari bilangan real.
![]()
Seperti yang Anda lihat, membuat fungsi bukanlah operasi yang mudah untuk dipahami. Oleh karena itu, kami menyarankan Anda berlatih latihan komposisi fungsi berikut:
➤ Lihat: menyelesaikan latihan tentang komposisi fungsi
Properti operasi dengan fungsi
Dari semua operasi dengan fungsi, jumlah dan hasil kali dicirikan oleh sifat-sifat berikut:
- Sifat asosiatif : Urutan penambahan atau perkalian 3 fungsi atau lebih tidak relevan.
![]()
![]()
- Sifat komutatif : urutan penjumlahan atau perkalian dua fungsi tidak mengubah hasilnya.
![]()
![]()
- Elemen netral: operasi penjumlahan dan operasi produk memiliki fungsi elemen netral yang konstan
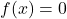
Dan
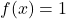
masing-masing.
- Elemen simetris : fungsi penjumlahan mempunyai fungsi kebalikannya
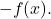
- Sifat distributif : sifat ini menghubungkan jumlah dan hasil kali operasi, dan didasarkan pada persamaan berikut:
![]()