Operasi dengan monomial

September 17, 2023

Di halaman ini kami menjelaskan cara melakukan semua operasi dengan monomial (penjumlahan, pengurangan, perkalian, pembagian, dan pangkat). Selain itu, Anda akan dapat melihat contoh setiap jenis operasi dengan monomial dan berlatih dengan latihan yang diselesaikan langkah demi langkah.

Penjumlahan dan pengurangan monomial

Dua atau lebih monomial hanya dapat dijumlahkan atau dikurangkan jika monomialnya serupa, yaitu jika kedua monomial tersebut mempunyai bagian literal yang identik (huruf dan eksponen yang sama).

Kemudian, jumlah (atau pengurangan) dari dua monomial serupa sama dengan monomial lain yang terdiri dari bagian literal yang sama dan jumlah (atau pengurangan) koefisien dari kedua monomial tersebut.

Penjumlahan dan pengurangan monomial disebut juga penjumlahan dan pengurangan monomial.

Contoh penjumlahan dan pengurangan monomial

Agar Anda dapat memahami dengan jelas cara menjumlahkan dan mengurangkan dua monomial atau lebih, kami berikan beberapa contoh di bawah ini:

$4x^6+3x^6 = 7x^6$
$5y^3-2y^3 = 3y^3$
$2x^2y+5x^2y-3x^2y = 4x^2y$
$6abc-7abc+4abc = 3abc$
$6x^3y^2-4x^3y+2x^2y^3 = \color{red} \bm{\times}$

Monomial pada contoh terakhir tidak dapat dijumlahkan atau dikurangkan karena tidak sejenis atau dengan kata lain mempunyai variabel yang tidak diketahui atau eksponennya berbeda.

Produk beberapa kali monomial

Untuk menyelesaikan perkalian monomial dengan suatu angka, kalikan saja koefisien monomial dengan angka tersebut, biarkan bagian literal dari monomial tersebut tetap sama.

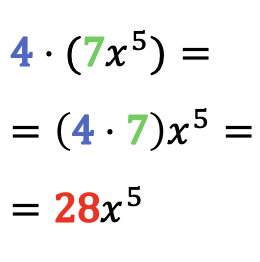
Contoh perkalian bilangan dengan monomial

$2\cdot (6x^3) = (2\cdot 6)x^3 = 12x^3$
$-4\cdot (5x^7) = (-4\cdot 5)x^7 = -20x^7$
$5\cdot (-3a^4b) = (5\cdot (-3))a^4b = -15a^4b$
$-7(-6x^9y^5)= (-7\cdot (-6))x^9y^5=42x^9y^5$

Perkalian monomial

Hasil perkalian dua monomial adalah monomial lain yang koefisiennya merupakan perkalian koefisien-koefisien monomial tersebut dan bagian literalnya diperoleh dengan mengalikan variabel-variabel yang mempunyai basis yang sama, yaitu dengan menjumlahkan eksponennya.

Oleh karena itu, untuk mengalikan dua monomial berbeda, kita harus mengalikan koefisien di antara keduanya dan menjumlahkan eksponen pangkat yang mempunyai basis yang sama.

Namun, jika kita mengalikan dua monomial dengan pangkat dasar berbeda , kita hanya perlu mengalikan koefisiennya dan membiarkan pangkatnya tetap sama. Misalnya:

$5x^2\cdot 3y^4 = (5\cdot 3) x^2y^4 = 15x^2y^4$

Sebaliknya, ketika mengalikan monomial, aturan tanda harus diperhatikan:

Monomial positif dikalikan dengan monomial positif menghasilkan monomial positif lainnya.
Monomial positif dikalikan dengan monomial negatif (atau sebaliknya) sama dengan monomial negatif.
Dua monomial negatif dikalikan menghasilkan monomial positif.

Contoh perkalian monomial

Di bawah ini beberapa contoh perkalian antar monomial agar Anda dapat melihat cara kerjanya:

$6x^4 \cdot 7x^5= (6\cdot 7)x^{4+5} = 42x^9$
$4y \cdot 2y^3 = (4\cdot 2)y^{1+3} = 8 y^4$
$5x^2y^4\cdot (-8x^8y^2)=(5\cdot (-8))x^{2+8}y^{4+2} = -40x^{10}y^6$
$-3x^6y^4 \cdot (-4x^2z)= (-3\cdot (-4)) x^{6+2}y^4z= 12x^8y^4z$
$-3x^8\cdot 4x^5\cdot (-x^2) =-12x^{13}\cdot (-x^2)= 12x^{15}$

Seperti yang Anda lihat, menyelesaikan perkalian monomial relatif sederhana. Namun perlu diingat bahwa monomial juga dapat dikalikan dengan polinomial, dan bahkan 2 polinomial atau lebih dapat dikalikan. Jika Anda lebih tertarik, Anda dapat melihat cara kerja semua operasi ini dengan mengklik perkalian polinomial .

Pembagian monomial

Dalam matematika, hasil pembagian monomial adalah monomial lain yang koefisiennya setara dengan hasil bagi koefisien monomial dan bagian literalnya diperoleh dengan membagi variabel-variabel yang mempunyai basis yang sama, yaitu dengan mengurangkan eksponennya. .

Jelasnya, setiap pembagian monomial juga dapat dinyatakan sebagai pecahan:

$8x^3y^2z : 2x^2y = \cfrac{8x^3y^2z}{2x^2y} = 4xyz$

Seperti halnya perkalian, dalam pembagian monomial perlu diterapkan hukum tanda:

Monomial positif dibagi dengan monomial positif menghasilkan monomial positif lainnya.
Monomial positif dibagi dengan monomial negatif (atau sebaliknya) setara dengan monomial negatif.
Dua monomial negatif yang dibagi satu sama lain menghasilkan monomial positif.

Contoh pembagian monomial

Anda dapat melihat lebih banyak contoh pembagian dua monomial atau lebih di bawah ini:

$7x^6 : 7x^4= (7:7)x^{6-4} = 1x^2=x^2$
$12y^5 : 4y^2= (12:4)y^{5-2} = 3y^3$
$15x^7y^6 :3x^4y^5= (15:3)x^{7-4}y^{6-5} = 5x^3y$
$27x^9y^7 :(-3x^5y^2)= (27:(-3))x^{9-5}y^{7-2}= -9x^4y^5$
$-18x^{13} : 3x^4 : (-2x^7) = -6x^9: (-2x^7) = 3x^2$

Tentunya suatu saat, ketika Anda mempelajari sesuatu yang baru dalam matematika, Anda bertanya pada diri sendiri: untuk apa ? Nah, pembagian monomial digunakan untuk membagi polinomial. Faktanya, sering terjadi kesalahan dalam membagi polinomial karena dua monomial salah dibagi. Oleh karena itu kami menganjurkan agar, setelah Anda memahami pembagian antar monomial, Anda melihat cara penghitungan pembagian polinomial , karena sekarang akan lebih mudah bagi Anda untuk mempelajari prosedurnya (cukup rumit).

Kekuatan monomial

Dalam matematika, untuk menghitung pangkat suatu monomial, setiap elemen monomial dipangkatkan . Dengan kata lain, pangkat monomial terdiri dari menaikkan koefisien dan variabelnya (huruf) menjadi eksponen pangkatnya.

bagaimana operasi dengan monomial diselesaikan

Ingatlah dari sifat-sifat pangkat bahwa ketika keduanya menaikkan suku yang sudah tinggi, eksponennya berlipat ganda. Oleh karena itu , pangkat monomial, pangkat setiap huruf selalu dikalikan dengan pangkat yang menunjukkan pangkat .

Di sisi lain, untuk melaksanakan operasi ini dengan benar, Anda harus mengingat properti kekuasaan berikut:

Monomial negatif yang dipangkatkan menjadi eksponen genap setara dengan monomial positif.
Sebaliknya, monomial negatif yang dipangkatkan menjadi eksponen ganjil akan menghasilkan monomial negatif.

Contoh pangkat monomial

Kami memberikan beberapa contoh kepada Anda sehingga Anda dapat memahami dengan jelas cara menghitung pangkat monomial:

$\left(5x^6\right)^2 = 5^2\left(x^6\right)^2 = 5^2x^{6\cdot 2} = 25x^{12}$
$\left(2x^5\right)^4 = 2^4\left(x^5\right)^4 = 2^4x^{5\cdot 4} = 16x^{20}$
$\left(-4y^3\right)^2 = (-4)^2\left(y^3\right)^2 = (-4)^2y^{3\cdot 2} = 16y^{6}$
$\left(3x^4y\right)^3 = 3^3\left(x^4y\right)^3 = 3^3x^{4\cdot 3}y^{1\cdot 3} = 27x^{12}y^3$
$\left(-2a^5b^7\right)^3 = (-2)^3\left(a^5b^7\right)^3 = (-2)^3a^{5\cdot 3}b^{7\cdot 3} = -8a^{15}b^{21}$

Operasi dikombinasikan dengan monomial

Setelah Anda melihat semua operasi dengan monomial, ketahuilah bahwa mereka juga dapat digabungkan satu sama lain. Artinya, kita dapat menemukan latihan di mana kita diminta untuk menyelesaikan operasi dengan monomial yang melibatkan semua jenis: penjumlahan, pengurangan, perkalian, pembagian, dan pangkat.

Tapi jangan khawatir, ini tidak sesulit kelihatannya. Satu-satunya hal yang perlu Anda ingat adalah urutan penyelesaian operasi gabungan:

Pertama, operasi dengan monomial dalam tanda kurung diselesaikan.
Kemudian kekuatan monomial dihitung.
Ketiga, dilakukan perkalian dan pembagian monomial.
Dan terakhir, penjumlahan dan pengurangan monomial ditentukan.

Saya yakin dengan memecahkan sebuah contoh Anda akan melihatnya lebih jelas:

Contoh operasi gabungan monomial

$12x^9:(2x^4-8x^4)+3x^4\cdot 6x - (x^3\cdot 7x^2)$

Pertama-tama, kita harus menyelesaikan operasi dengan monomial dalam tanda kurung:

$12x^9:(-6x^4)+3x^4\cdot 6x - 7x^5$

Dalam hal ini, kami tidak punya kuasa. Sekarang mari kita hitung perkalian dan pembagian monomial:

$-2x^5+18x^5 - 7x^5$

Dan terakhir, kita menjumlahkan dan mengurangkan monomial:

$16x^5 - 7x^5$

$\bm{9x^5}$

Latihan soal operasi dengan monomial

Jika Anda ingin berlatih, kami tinggalkan beberapa latihan di bawah ini yang diselesaikan selangkah demi selangkah dari kesulitan ESO pada operasi dengan monomial.

Latihan 1

Hitung penjumlahan dan pengurangan monomial berikut:

$\text{A)} \ 2x^4+9x^4$

$\text{B)} \ -3x^5y^3 +4x^5y^3$

$\text{C)} \ 3x^8-6x^8+2x^8$

$\text{D)} \ -2a^3b^2-5a^3b^2+3a^3b^2-7a^3b^2+4a^3b^2$

$\text{E)} \ 6xyz-5xz-7xyz-8xz$

$\text{F)} \ 6y^3+2y^3-y^5+8y^4-y^5-5y^3$

Lihat solusinya

$\text{A)} \ 2x^4+9x^4= \bm{11x^4}$

$\text{B)} \ -3x^5y^3 +4x^5y^3= \bm{x^5y^3}$

$\text{C)} \ 3x^8-6x^8+2x^8= \bm{-x^8}$

$\text{D)} \ -2a^3b^2-5a^3b^2+3a^3b^2-7a^3b^2+4a^3b^2=\bm{-7a^3b^2}$

$\text{E)} \ 6xyz-5xz-7xyz-8xz= \bm{-xyz-13xz}$

$\text{F)} \ 6y^3+2y^3-y^5+8y^4-y^5-5y^3 = \bm{-2y^5+8y^4+3y^3}$

Latihan 2

Selesaikan perkalian monomial berikut:

$\text{A)} \ 5x^7\cdot 6x^2$

$\text{B)} \ 2y^8\cdot (-5y^6)$

$\text{C)} \ -4a^3 \cdot (-2a)$

$\text{D)} \ 2x^3\cdot 4x \cdot (-3x^6)$

$\text{E)} \ -5x^6\cdot (-x^3) \cdot (-9x^4)$

$\text{F)} \ 7x^3y^2 \cdot 5x^8z^4 \cdot (-2x^2y^5z^3)$

Lihat solusinya

$\text{A)} \ 5x^7\cdot 6x^2=(5\cdot 6)x^{7+2} = \bm{30x^9}$

$\text{B)} \ 2y^8\cdot (-5y^6)= (2\cdot (-5))y^{8+6} = \bm{-10y^{14}}$

$\text{C)} \ -4a^3 \cdot (-2a) =(-4\cdot (-2))a^{3+1} = \bm{8a^4}$

$\text{D)} \ 2x^3\cdot 4x \cdot (-3x^6) = 8x^4\cdot (-3x^6) = \bm{-24x^{10}}$

$\text{E)} \ -5x^6\cdot (-x^3) \cdot (-9x^4)=5x^9\cdot (-9x^4) =\bm{-45x^{13}}$

$\text{F)} \ 7x^3y^2 \cdot 5x^8z^4 \cdot (-2x^2y^5z^3)= <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-bb20ebb96e0dff759d07813f6fff9470_l3.png" height="22" width="195" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[35x^{11}y^2z^4\cdot (-2x^2y^5z^3) =\]" title="Rendered by QuickLaTeX.com"/> \bm{-70x^{13}y^7z^7}” title=”Rendered by QuickLaTeX.com”> <div class=$

Latihan 3

Tentukan hasil pembagian monomial berikut:

$\text{A)} \ 24x^4: 6x^2$

$\text{B)} \ 16a^9: (-2a^6)$

$\text{C)} \ -21x^3:(-3x)$

$\text{D)} \ 14x^8y^3 :2x^6y$

$\text{E)} \ 42x^5y^3z^6 : 7x^2y^3z^4$

$\text{F)} \ 48x^8y^6z^{10} : (-6x^4y^{2}z^4) : (-4x^2y^2z^3)$

Lihat solusinya

$\text{A)} \ 24x^4: 6x^2 = (24:6)x^{4-2} = \bm{4x^2}$

$\text{B)} \ 16a^9: (-2a^6)= (16:(-2))a^{9-6} = \bm{-8a^3}$

$\text{C)} \ -21x^3:(-3x) = (-21:(-3))x^{3-1} = \bm{7x^2}$

$\text{D)} \ 14x^8y^3 :2x^6y = \bm{7x^2y^2}$

$\text{E)} \ 42x^5y^3z^6 : 7x^2y^3z^4= 6x^3y^0z^2=\bm{6x^3z^2}$

Pada operasi sebelumnya kami menyederhanakan istilah tersebut

$y^0$

karena bilangan apa pun yang dipangkatkan ke 0 sama dengan 1. Jadi:

$6x^3y^0z^2=6x^3\cdot 1 \cdot z^2=\bm{6x^3z^2}$

$\text{F)} \ 48x^8y^6z^{10} : (-6x^4y^{2}z^4) : (-4x^2y^2z^3)= <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-6dc0e068dbf84cef6abfe7e1789d245b_l3.png" height="22" width="194" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[-8x^4y^4z^6: (-4x^2y^2z^3)=\]" title="Rendered by QuickLaTeX.com"/> \bm{2x^2y^2z^3}” title=”Rendered by QuickLaTeX.com”> <div class=$

Latihan 4

Temukan pangkat monomial berikut:

$\text{A)} \ \left(-8x^4\right)^2$

$\text{B)} \ \left(-2a^7\right)^3$

$\text{C)} \ \left(5x^8y^2\right)^3$

$\text{D)} \ \left(-x^3y^5z\right)^6$

$\text{E)} \ \left(-2x^5y^4\right)^5$

Lihat solusinya

$\text{A)} \ \left(-8x^4\right)^2=(-8)^2\left(x^4\right)^2 = (-8)^2x^{4\cdot 2} = \bm{64x^{8}}$

$\text{B)} \ \left(-2a^7\right)^3=(-2)^3\left(a^7\right)^3 = (-2)^3a^{7\cdot 3} = \bm{-8a^{21}}$

$\text{C)} \ \left(5x^8y^2\right)^3=(5)^3\left(x^8y^2\right)^3 = \bm{125x^{24}y^6}$

$\text{D)} \ \left(-x^3y^5z\right)^6=(-1)^6\left(x^3y^5z\right)^6 = \bm{x^{18}y^{30}z^{6}}$

$\text{E)} \ \left(-2x^5y^4\right)^5 =(-2)^5\left(x^5y^4\right)^5 = \bm{-32x^{25}y^{20}}$

Latihan 5

Selesaikan operasi berikut yang digabungkan dengan monomial dan sederhanakan sebanyak mungkin:

$\text{A)} \ 3x^2\cdot 4x^5 : 2x^4 + 10x^6:(-2x^4)\cdot 6x$

$\text{B)} \ 4\cdot \left(5x^4 -2x^4\right)^2$

$\text{C)} \ 8x^7:(-4x^3+3x^3-7x^3)-5x^3\cdot 3x$

$\text{D)} \ \left(-2x^2y\right)^3+4x^2 \cdot 5\left(xy\right)^4:(-2y)$

$\text{E)} \ 8x^8:\left(-2x^3\right)^2-(7x^3\cdot 6x^6): (-2x^4)$

Lihat solusinya

$\color{blue} \mathbf{A}\bm{)} \color{black} \ 3x^2\cdot 4x^5 : 2x^4 + 10x^6:(-2x^4)\cdot 6x$

$12x^7 : 2x^4 -5x^2\cdot 6x$

$6x^3 -30x^3$

$\bm{-24x^3}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ 4\cdot \left(5x^4 -2x^4\right)^2$

$4\cdot \left(3x^4 \right)^2$

$4\cdot 9x^8$

$\bm{36x^8}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ 8x^7:(-4x^3+3x^3-7x^3)-5x^3\cdot 3x$

$8x^7:(-8x^3)-5x^3\cdot 3x$

$-x^4-15x^4$

$\bm{-16x^4}$

$\color{blue} \mathbf{D}\bm{)} \color{black} \ \left(-2x^2y\right)^3+4x^2 \cdot 5\left(xy\right)^4:(-2y)$

$-8x^6y^3+4x^2 \cdot 5\cdot x^4y^4:(-2y)$

$-8x^6y^3+4x^2 \cdot 5x^4y^4:(-2y)$

$-8x^6y^3+20x^6y^4:(-2y)$

$-8x^6y^3-10x^6y^3$

$\bm{-18x^6y^3}$

$\color{blue} \mathbf{E}\bm{)} \color{black} \ 8x^8:\left(-2x^3\right)^2-(7x^3\cdot 6x^6): (-2x^4)$

$8x^8:\left(-2x^3\right)^2-42x^9: (-2x^4)$

$8x^8:4x^6-42x^9: (-2x^4)$

$\bm{2x^2+21x^5}$

Pengoperasiannya tidak dapat disederhanakan lagi karena kedua monomial mempunyai eksponen yang berbeda, sehingga hasilnya adalah polinomial.

Jika Anda sudah sampai sejauh ini, berarti Anda sudah menguasai semua operasi dengan monomial. Terang! Nah, operasi lain yang pasti menarik bagi Anda adalah faktorial suatu bilangan. Ini adalah operasi yang agak aneh, karena perhitungannya berbeda dari operasi lainnya. Dan nyatanya masih banyak orang yang belum mengetahui apa itu faktorial suatu bilangan. Cari tahu cara menyelesaikan faktorial dengan mengklik tautan ini.

Penjumlahan dan pengurangan monomial

Contoh penjumlahan dan pengurangan monomial

Produk beberapa kali monomial

Contoh perkalian bilangan dengan monomial

Perkalian monomial

Contoh perkalian monomial

Pembagian monomial

Contoh pembagian monomial

Kekuatan monomial

Contoh pangkat monomial

Operasi dikombinasikan dengan monomial

Contoh operasi gabungan monomial

Latihan soal operasi dengan monomial

Latihan 1

Latihan 2

Latihan 3

Latihan 4

Latihan 5

Tinggalkan Komentar Batalkan Balasan