Angka Pi adalah konstanta matematika yang mewakili hubungan antara keliling lingkaran dan diameternya. Itu adalah angka yang tidak masuk akal. Dengan kata lain, ini bukanlah pecahan eksak . Oleh karena itu, ini tidak dapat direpresentasikan sebagai bilangan desimal berhingga. Nilai Pi kira-kira 3,14159 dan dilambangkan dengan huruf Yunani π.
Pi adalah angka penting dalam matematika. Oleh karena itu, ia memiliki banyak penerapan di berbagai bidang. Misalnya, digunakan dalam geometri untuk menghitung luas. Juga keliling lingkaran dan bangun datar lainnya. Sebaliknya, dalam trigonometri untuk menghitung sudut dan panjang busur. Terakhir, di bidang teknik dan fisika untuk menghitung besaran seperti volume dan kapasitas.
Hari Pi diperingati setiap tanggal 14 Maret karena tanggal tersebut mendekati nilai Pi (3,14). Tanggal ini dirayakan untuk memperingati peran Pi dalam matematika dan meningkatkan minat terhadap konstanta fundamental ini.
Siapa yang menemukan bilangan Pi?
Angka Pi telah dikenal sejak jaman dahulu, dan matematikawan Yunani Archimedes (287-212 SM)lah yang mendeskripsikannya dengan tepat. Bahkan, ia menggunakannya untuk menghitung luas dan volume bangun geometri.
Pada abad ke-18, matematikawan Swiss Johann Lambert membuktikan bahwa Pi adalah bilangan irasional . Belakangan, pada abad ke-19, matematikawan Jerman Ferdinand von Lindemann menjelaskan bahwa Pi adalah bilangan transendental . Artinya, tidak dapat dinyatakan sebagai solusi eksak persamaan polinomial dengan koefisien rasional.
Sepanjang sejarah, berbagai ahli matematika telah berkontribusi dalam memahami bilangan Pi dan mengembangkan teknik untuk menghitungnya dengan lebih presisi. Saat ini, Pi tetap menjadi salah satu konstanta matematika terpenting dan paling terkenal di dunia dan terus menjadi subjek studi matematika.
Mengapa bilangan Pi tidak terbatas?
Nilai Pi kira-kira 3,14159, namun kenyataannya ini adalah angka yang terus berlanjut tanpa batas waktu setelah koma. Artinya Pi adalah bilangan tak terhingga dan tidak dapat seluruhnya diwakili oleh bilangan desimal.
Meskipun nilai Pi tidak terhingga, dalam praktiknya nilai perkiraan Pi dapat dihitung dengan sangat presisi. Saat ini, jutaan digit Pi telah dihitung dan terbukti bahwa ia tidak memiliki pola teratur dalam angka desimalnya. Meskipun ini dilakukan melalui superkomputer karena kami tidak dapat menghitung angka sebanyak itu.
Metode apa yang ada untuk menghitung perkiraan nilai bilangan Pi?
Ada beberapa metode praktis untuk menghitung nilai Pi. Selanjutnya, kami menjelaskan langkah demi langkah tiga metode yang paling banyak digunakan oleh para ahli matematika.
1. Metode Archimedes
Ahli matematika Yunani Archimedes menggunakan metode geometri untuk menghitung perkiraan nilai Pi. Untuk menggunakan metode ini, ikuti langkah-langkah di bawah ini:
1. Gambarlah sebuah lingkaran dan tarik garis melalui pusat lingkaran dan potong di dua titik yang berlawanan seperti gambar di bawah ini:
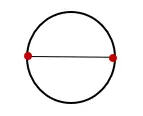
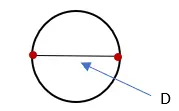
2. Ukur panjang garis yang memotong lingkaran dan beri label “D”. Pengukuran ini adalah diameter lingkaran.
3. Ukur panjang garis yang membentuk lingkaran dan beri label “C”. Pengukuran ini adalah keliling lingkaran.
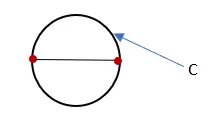
4. Bagilah keliling lingkaran (C) dengan diameter lingkaran (D). Hasilnya adalah perkiraan nilai Pi.
Contoh: jika diameter lingkaran adalah 6 dan kelilingnya adalah 18, maka perkiraan nilai Pi adalah 18 6 = 3. Tentu saja contoh ini sangat mendasar, tetapi jika Anda melakukannya dengan nilai keliling sebenarnya , Anda akan melihat bahwa metode ini berfungsi dengan benar.
Faktanya, kami menyarankan untuk mencobanya: ukur cangkir atau sesuatu yang berbentuk lingkaran dan lihat apakah itu cocok untuk Anda.
2. Metode Monte Carlo
Metode Monte Carlo adalah metode probabilistik yang digunakan untuk menghitung perkiraan nilai Pi. Untuk melakukan ini, sejumlah besar titik dihasilkan secara acak pada sebuah bidang dan jumlah titik yang sesuai dengan lingkaran yang tertulis dalam persegi dihitung. Prosesnya diterapkan sebagai berikut:
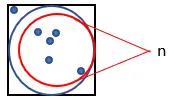
1. Gambarlah sebuah lingkaran di dalam persegi dengan sisi 1, seperti gambar di bawah ini:

2. Hasilkan sejumlah besar titik dalam kotak secara acak.
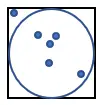
3. Hitung jumlah titik yang masuk ke dalam lingkaran. Sebut saja besaran ini “n”.
4. Hitung jumlah poin yang dihasilkan. Sebut besaran ini “m”.
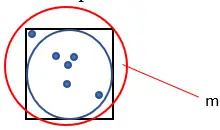
5. Hitung perkiraan nilai Pi menggunakan rumus berikut: Pi = (4 · n) ± m.
Misalnya, jika 380 titik dihasilkan dan 300 titik masuk ke dalam lingkaran, maka perkiraan nilai Pi adalah (4 · 300) 380 = 3,16. Nilai ini sangat mirip dengan dua desimal pertama Pi, namun sama seperti metode sebelumnya, menggunakan pengukuran aktual akan memberi Anda nilai yang lebih tepat .
3. Metode iterasi
Metode iterasi merupakan suatu metode matematis yang digunakan untuk menghitung perkiraan nilai Pi. Metode ini menggunakan rumus yang menyiratkan nilai Pi dan diterapkan secara iteratif untuk meningkatkan keakuratan perhitungan. Berikut langkah-langkah untuk menggunakan metode ini:
- Pilih nilai awal untuk Pi. Misalnya, Anda dapat memilih nilai 3.
- Gunakan rumus yang melibatkan nilai Pi untuk menghitung nilai perkiraan baru. Misalnya, Anda bisa menggunakan rumus berikut: Pi = (Pi + (4 ÷ Pi)) ÷ 2
- Bandingkan nilai perkiraan baru dengan nilai lama. Jika perbedaan antara keduanya cukup kecil, maka Anda telah mendapatkan hasil yang akurat. Jika perbedaannya masih signifikan, tetapkan nilai baru ke Pi dan ulangi proses dari langkah 2.
Misalnya, jika nilai awal Pi adalah 3, nilai perkiraan barunya adalah (3 + (4 3)) 2 = 2,66666666. Namun, karena perbedaan keduanya tidak terlalu kecil , Anda selalu dapat mengulangi proses tersebut beberapa kali sebelum menemukan nilai yang akurat.
Apa saja kegunaan bilangan Pi?
Pi merupakan bilangan penting dalam matematika dan memiliki banyak penerapan di berbagai bidang. Di antara aplikasi Pi yang paling penting, kami memiliki yang berikut ini:
Geometri
Pi digunakan dalam geometri untuk menghitung luas dan keliling lingkaran dan bangun lingkaran lainnya:
- Lingkaran : Menghitung luas dan keliling lingkaran.
- Bola : menentukan luas dan volume bola.
- Silinder : Perhitungan luas permukaan dan volume silinder.
- Kerucut – Digunakan untuk menghitung luas permukaan dan volume kerucut.
Trigonometri
Hal ini berguna dalam trigonometri untuk menghitung sudut dan panjang busur. Beberapa penerapannya adalah:
- Sudut : perhitungan sudut dan panjang busur.
- Fungsi Trigonometri – Digunakan untuk menghitung nilai fungsi trigonometri untuk sudut tertentu.
- Trigonometri lingkaran : untuk menghitung nilai fungsi trigonometri sudut 360 derajat.
Rekayasa
Dalam bidang teknik, Pi digunakan dalam menghitung besaran seperti volume dan kapasitas. Beberapa penerapannya adalah:
- Elektronik : menghitung besaran seperti resistansi dan kapasitansi.
- Listrik : digunakan untuk menghitung besaran seperti daya dan energi listrik.
- Teknik sipil : menghitung besaran seperti luas permukaan dan volume struktur dan elemen konstruksi.
Fisik
Bilangan Pi (π) merupakan konstanta matematika yang memiliki banyak penerapan dalam fisika. Berikut beberapa contoh penggunaan Pi dalam fisika:
- Gelombang – Digunakan untuk menghitung frekuensi dan panjang gelombang gelombang.
- Mekanika : Dalam mekanika, berguna untuk menghitung usaha dan energi dalam sistem berputar.
- Elektromagnetisme : Dalam elektromagnetisme, dapat digunakan untuk menghitung energi yang tersimpan dalam kapasitor dan induktansi dalam belitan.
- Kosmologi Dalam kosmologi, Pi digunakan untuk menghitung kelengkungan ruang-waktu dan perluasan alam semesta.
Penerapan apa yang dimiliki angka Pi dalam kehidupan nyata?
Berikut beberapa contoh penggunaan Pi dalam kehidupan sehari-hari:
- Geometri : untuk menentukan luas alas berbentuk lingkaran atau untuk mengukur panjang pita pengukur yang diperlukan untuk menutupi keliling meja berbentuk lingkaran.
- Memasak – menentukan berapa banyak air atau cairan yang dibutuhkan untuk mengisi panci atau berapa banyak bahan yang dapat dimasukkan ke dalam wadah melingkar.
- Astronomi : mengetahui jarak planet dan bintang, orbit planet, dan kedudukan benda langit di langit.
- Berkebun : Mengetahui jumlah tanah atau tanah yang dibutuhkan untuk mengisi pot berbentuk lingkaran atau untuk menghitung jumlah air yang dibutuhkan untuk menyiram tanaman pada taman berbentuk lingkaran.