Nol ketidakpastian antara nol (0/0)

Pada artikel ini kami menjelaskan cara menyimpan limit suatu fungsi ketika memberikan ketidakpastian 0/0. Selain itu, Anda akan dapat berlatih dengan latihan yang diselesaikan tentang ketidakpastian nol antara nol.

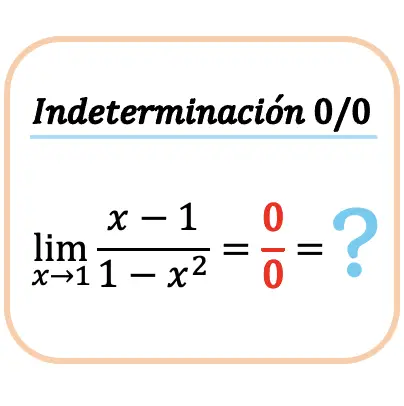
Bagaimana mengatasi ketidakpastian nol antara nol (0/0)

Kita kemudian akan melihat cara menghitung limit suatu fungsi ketika fungsi tersebut memberikan ketidakpastian nol antara nol (0/0). Untuk melakukan ini, kami akan menghitung contoh langkah demi langkah:

\displaystyle\lim_{x \to 2} \frac{x^2-x-2}{x^2-3x+2}

Pertama-tama kita mencoba menghitung limit dengan mensubstitusikan nilai x ke dalam fungsi:

\displaystyle\lim_{x \to 2} \frac{x^2 - x -2}{x^2-3x+2}=\frac{2^2 -2-2}{2^2-3\cdot 2+2}=\frac{0}{0}

Tapi kita mendapatkan ketidakpastian 0 dibagi 0.

Jika limit suatu fungsi titik memberikan ketidakpastian 0/0 , polinomial pembilang dan penyebutnya perlu difaktorkan, kemudian faktor persekutuannya disederhanakan.

Oleh karena itu, kita harus memfaktorkan polinomial pembilang dan penyebut pecahan tersebut. Untuk melakukan ini, kami menggunakan aturan Ruffini:

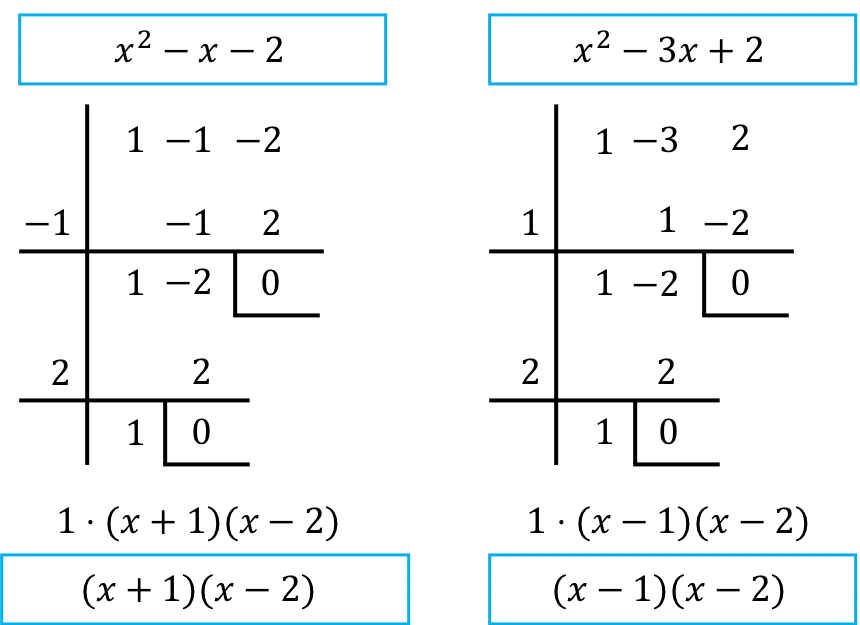
faktorisasi ketidakpastian 0/0

➤ Jika Anda tidak tahu cara memfaktorkan suatu polinomial , kami sarankan Anda melihat penjelasannya di situs kami khusus polinomial: www.polinomios.org

Jadi, setelah polinomial difaktorkan, limitnya adalah sebagai berikut:

\displaystyle\lim_{x \to 2} \cfrac{x^2-x-2}{x^2-3x+2}=\lim_{x \to 2}\frac{(x+1)(x-2)}{(x-1)(x-2)}

Sekarang kita dapat menyederhanakan limitnya dengan menghilangkan faktor-faktor yang berulang pada pembilang dan penyebut pecahan:

\displaystyle\lim_{x \to 2} \cfrac{(x+1)\cancel{(x-2)}}{(x-1)\cancel{(x-2)}}=\lim_{x \to 2} \cfrac{(x+1)}{(x-1)}

Dan terakhir, kami menghitung ulang batasnya:

\displaystyle\lim_{x \to 2} \cfrac{x+1}{x-1}=\cfrac{2+1}{2-1}=\cfrac{3}{1}=\bm{3}

Seperti yang Anda lihat, setelah kita memfaktorkan dan menyederhanakan polinomial, sangat mudah untuk menemukan solusi dalam limitnya.

Ketidakpastian 0/0 dengan akar

Kita baru saja melihat bagaimana ketidakpastian 0/0 dari fungsi rasional diselesaikan. Namun, jika limitnya merupakan fungsi yang tidak rasional (atau radikal), maka ketidakpastian 0/0 diselesaikan secara berbeda.

\displaystyle\lim_{x \to 1} \frac{x-1}{\sqrt{x}-1}

Pertama, kami mencoba menyelesaikan batasan tersebut dengan melakukan operasi berikut:

\displaystyle\lim_{x \to 1} \frac{x-1}{\sqrt{x}-1}=\frac{1-1}{\sqrt{1}-1}=\frac{0}{0}

Tapi kita mendapatkan ketidakpastian yang nol di atas nol.

Jika limit suatu fungsi dengan akar memberikan ketidakpastian 0/0 , Anda harus mengalikan pembilang dan penyebut pecahan dengan konjugat dari ekspresi akarnya.

➤ Ingatlah bahwa konjugatnya adalah ekspresi irasional yang sama tetapi dengan tanda tengahnya dimodifikasi.

Selanjutnya, kita mengalikan pembilang dan penyebut pecahan dengan konjugat dari ekspresi radikal:

\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}+1\right)}

Dalam batasan seperti ini, dengan melakukan langkah ini kita akan selalu memperoleh identitas penting yang dapat kita sederhanakan. Dalam hal ini, dalam penyebut kita memiliki hasil kali jumlah dan selisih, oleh karena itu:

\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{\left(\sqrt{x}\right)^2-1^2}

\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{x-1}

Kita sederhanakan faktor yang berulang pada pembilang dan penyebutnya:

\displaystyle\lim_{x \to 1} \frac{\cancel{\left(x-1\right)}\cdot\left(\sqrt{x}+1\right)}{\cancel{x-1}}=\lim_{x \to 1}\left(\sqrt{x}+1\right)

Dan dengan cara ini kita dapat mengetahui hasil limitnya:

\displaystyle\lim_{x \to 1}\left(\sqrt{x}+1\right)=\sqrt{1}+1=2

Latihan terpecahkan tentang ketidakpastian 0/0

Di bawah ini kami telah menyiapkan beberapa latihan penyelesaian langkah demi langkah tentang limit fungsi yang memberikan ketidakpastian 0/0. Anda dapat mencoba melakukannya dan kemudian memeriksa solusinya.

Jangan lupa bahwa Anda dapat mengajukan pertanyaan apa pun kepada kami tentang penyelesaian batasan di komentar!

Latihan 1

Hitung limit fungsi rasional berikut di titik x=-2.

\displaystyle\lim_{x \to -2}\frac{x^2 +2x}{x^2-x-6}

Logikanya, pertama-tama kita coba selesaikan limitnya:

\displaystyle\lim_{x \to -2} \frac{x^2 +2x}{x^2-x-6}=\frac{(-2)^2+2\cdot (-2)}{(-2)^2-(-2)-6}=\frac{4-4}{4+2-6}=\frac{0}{0}

Tapi kita berakhir dengan ketidakpastian 0/0. Oleh karena itu, kita harus memfaktorkan polinomial pembilang dan penyebutnya:

\displaystyle\lim_{x \to -2}\frac{x^2 +2x}{x^2-x-6}=\lim_{x \to -2}\frac{x(x+2)}{(x+2)(x-3)}

Sekarang kita sederhanakan pecahan dengan menghilangkan tanda kurung yang berulang pada pembilang dan penyebutnya:

\displaystyle\lim_{x \to -2}\frac{x\cancel{(x+2)}}{\cancel{(x+2)}(x-3)}=\lim_{x \to -2}\frac{x}{x-3}

Dan terakhir, kita menghitung ulang limitnya dengan pecahan yang disederhanakan:

\displaystyle\lim_{x \to -2}\frac{x}{x-3}=\cfrac{-2}{-2-3}=\cfrac{-2}{-5}=\mathbf{\cfrac{2}{5}}

Latihan 2

Selesaikan limit fungsi berikut ketika x mendekati -1:

\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}

Kita coba selesaikan dulu limitnya seperti biasa:

\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}=\frac{(-1)^3+2(-1)^2-(-1)-2}{(-1)^3-5(-1)^2+2(-1)+8} =\frac{0}{0}

Namun kita memperoleh ketidakpastian 0 antara 0. Oleh karena itu, kita harus memfaktorkan 2 polinomial pecahan tersebut:

\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}=\lim_{x \to -1}\frac{(x-1)(x+1)(x+2)}{(x+1)(x-2)(x-4)}

Sekarang kita dapat menyederhanakan polinomial:

\displaystyle\lim_{x \to -1}\frac{(x-1)\cancel{(x+1)}(x+2)}{\cancel{(x+1)}(x-2)(x-4)}=\lim_{x \to -1}\frac{(x-1)(x+2)}{(x-2)(x-4)}

Dan kami memecahkan batasnya:

\displaystyle\lim_{x \to -1} \frac{(x-1)(x+2)}{(x-2)(x-4)}=\frac{ (-1-1)(-1+2)}{(-1-2)(-1-4)}=\frac{(-2)\cdot (1)}{(-3)\cdot (-5)}=\frac{\bm{-2}}{\bm{15}}

Latihan 3

Tentukan penyelesaian limit fungsi radikal berikut:

\displaystyle\lim_{x\to 2}\frac{x^2-3x+2}{2-\sqrt{2x}}

Pertama, kita periksa apakah limitnya memberikan semacam ketidakpastian:

\displaystyle\lim_{x\to 2}\frac{x^2-3x+2}{2-\sqrt{2x}}=\frac{2^2-3\cdot2+2}{2-\sqrt{2\cdot 2}}=\frac{4-6+2}{2-2}=\frac{0}{0}

Batasnya memberikan ketidakpastian nol dibagi nol dan kita memiliki akar dalam fungsi tersebut. Oleh karena itu, kita harus mengalikan pembilang dan penyebut pecahan dengan konjugat dari persamaan akarnya:

\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{\left(2-\sqrt{2x}\right)\cdot \left(2+\sqrt{2x}\right)}

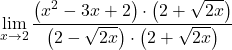
Penyebutnya sesuai dengan perkembangan identitas penting dari hasil kali penjumlahan dan selisih, oleh karena itu kita dapat menyederhanakannya:

\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{2^2-\left(\sqrt{2x}\right)^2}

\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{4-2x}

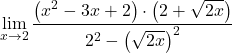
Namun kita belum bisa menyederhanakan suku-suku pecahan tersebut. Oleh karena itu kita harus memfaktorkan polinomialnya:

\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{4-2x}=\lim_{x\to 2}\frac{(x-1)(x-2)\cdot\left(2+\sqrt{2x}\right)}{-2(x-2)}

Dengan cara ini kita dapat menyederhanakan pecahan:

\displaystyle\lim_{x\to 2}\frac{(x-1)\cancel{(x-2)}\left(2+\sqrt{2x}\right)}{-2\cancel{(x-2)}}=\lim_{x\to 2}\frac{(x-1)\left(2+\sqrt{2x}\right)}{-2}

Dan sekarang kita dapat menentukan hasil limitnya:

\displaystyle\lim_{x\to 2}\frac{(x-1)\left(2+\sqrt{2x}\right)}{-2}=\frac{(2-1)\left(2+\sqrt{2\cdot 2}\right)}{-2}=\frac{1\cdot (2+2)}{-2}=\bm{-2}

Latihan 4

Hitung limitnya ketika x mendekati 0 dari fungsi radikal berikut:

\displaystyle\lim_{x\to 0}\frac{x^2+6x}{3-\sqrt{4x+9}}

Pertama, kita mencoba menghitung limit fungsi seperti yang selalu kita lakukan:

\displaystyle\lim_{x\to 0}\frac{x^2+6x}{3-\sqrt{4x+9}}=\frac{0+0}{3-\sqrt{4\cdot 0+9}}=\frac{0}{3-3}=\frac{0}{0}

Tapi kita mendapatkan bentuk tak tentu dari 0/0. Oleh karena itu, kita mengalikan pembilang dan penyebut fungsi tersebut dengan konjugasi ekspresi irasional:

\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{\left(3-\sqrt{4x+9}\right)\cdot\left(3+\sqrt{4x+9}\right)}

Kami menerapkan rumus identitas penting yang sesuai untuk menyederhanakan penyebutnya:

\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{3^2-\left(\sqrt{4x+9}\right)^2}

\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{9-(4x+9)}

\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{-4x}

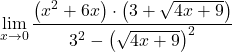
Sekarang kita faktorkan binomial pembilangnya dengan mengambil faktor persekutuannya:

\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{-4x}=\lim_{x\to 0}\frac{\bigl[x(x+6)\bigr]\cdot\left(3+\sqrt{4x+9}\right)}{-4x}

Mari kita sederhanakan faktor-faktor yang berulang pada pembilang dan penyebut fungsi tersebut:

\displaystyle\lim_{x\to 0}\frac{\cancel{x}\left(x+6\right)\left(3+\sqrt{4x+9}\right)}{-4\cancel{x}}=\lim_{x\to 0}\frac{(x+6)\left(3+\sqrt{4x+9}\right)}{-4}

Dan terakhir, kita menyelesaikan limit fungsinya:

\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{(x+6)\left(3+\sqrt{4x+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{(0+6)\left(3+\sqrt{4\cdot 0+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{6\cdot (3+3)}{-4}=\frac{36}{-4}=\bm{-9}\end{array}

Latihan 5

Selesaikan limit berikut dengan menggunakan metode ketidakpastian 0/0:

\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}

➤ Lihat: cara menghitung batas lateral suatu fungsi

Kami pertama-tama mencoba menyelesaikan batasannya:

\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}=\frac{(-1)^3+2(-1)^2-(-1)-2}{(-1)^3+5(-1)^2+7(-1)+3}=\frac{0}{0}

Namun dalam batas tersebut kita memperoleh ketidakpastian zero-on-zero. Oleh karena itu, kita memfaktorkan polinomial pembilang dan penyebutnya:

\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}=\lim_{x \to -1}\frac{(x-1)(x+1)(x+2)}{(x+1)^2(x+3)}

Sekarang kita sederhanakan pecahan dengan menghilangkan faktor yang berulang pada pembilang dan penyebutnya:

\displaystyle\lim_{x \to -1} \cfrac{(x-1)\cancel{(x+1)}(x+2)}{(x+1)^{\cancel{2}}(x+3)}=\lim_{x \to -1}\cfrac{(x-1)(x+2)}{(x+1)(x+3)}

Dan kami menghitung batasnya lagi:

\displaystyle\lim_{x \to -1}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)(-1+2)}{(-1+1)(-1+3)}=\frac{-2\cdot 1}{0 \cdot 2}=\frac{-2}{0} =\infty

Namun sekarang kita dihadapkan pada ketidakpastian suatu bilangan dibagi 0. Oleh karena itu, kita harus menghitung limit lateral fungsi tersebut ketika x cenderung -1.

Pertama-tama kita selesaikan limit lateral fungsi tersebut di titik x=-1 di sebelah kiri:

\displaystyle\lim_{x \to -1^{-}}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)\cdot (-1+2)}{(-1+1)\cdot (-1+3)}=\frac{-2}{-0}=+\infty

Lalu kita hitung limit lateral fungsi tersebut di titik x=-1 di sebelah kanan:

\displaystyle\lim_{x \to -1^{+}}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)\cdot (-1+2)}{(-1+1)\cdot (-1+3)}=\frac{-2}{+0}=-\infty

Oleh karena itu, karena kedua batas lateralnya tidak berimpit, maka batas fungsi di x=-1 tidak ada:

\displaystyle\displaystyle \lim_{x \to -1^-}f(x)= +\infty\neq\lim_{x \to -1^+}f(x)=-\infty\ \bm{\longrightarrow} \ \cancel{\exists} \lim_{x \to -1} f(x)

Tinggalkan Komentar

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *

Scroll to Top