Di halaman ini Anda akan mengetahui apa itu dan bagaimana cara menghitung nilai numerik suatu polinomial. Selain itu, Anda akan dapat melihat contoh dan latihan yang diselesaikan selangkah demi selangkah dari nilai numerik suatu polinomial.
Berapa nilai numerik polinomial?
Dalam matematika, nilai numerik suatu polinomial P(x) untuk nilai x=a, yaitu P(a), adalah hasil yang diperoleh dengan mengganti variabel x dari polinomial tersebut dengan bilangan a dan melakukan perhitungan yang ditunjukkan dalam ekspresi polinomial.
Agar Anda dapat lebih memahami konsep nilai numerik suatu polinomial, di bawah ini kami tunjukkan cara menghitungnya dengan sebuah contoh:
Cara menghitung nilai numerik polinomial
Sekarang setelah kita mengetahui definisi matematis dari nilai numerik suatu polinomial, mari kita lihat cara menentukan nilai numerik suatu polinomial menggunakan sebuah contoh:
- Berapakah nilai numerik polinomial berikut untuk x=2?
![]()
Untuk mencari nilai numerik suatu polinomial, polinomial tersebut perlu dievaluasi dengan nilai yang diberikan oleh soal, yaitu perlu mensubstitusikan variabel tersebut.
![]()
polinomial dengan nilai pernyataan. Oleh karena itu, dalam hal ini kita perlu mengganti surat tersebut
![]()
Untuk 2:
![]()
Dan setelah kita mengganti nilainya ke dalam ekspresi aljabar polinomial, kita melakukan operasinya. Jadi pertama-tama kita selesaikan kekuatannya:
![]()
Sekarang kita menghitung perkaliannya:
![]()
Dan terakhir, kita menjumlahkan dan mengurangi suku-sukunya:
![]()
Kesimpulannya, nilai numerik polinomial untuk x=2 sama dengan 21.
Seperti yang Anda lihat, mencari nilai numerik suatu polinomial tidak terlalu rumit, namun memiliki beberapa penerapan yang sangat berguna. Misalnya, mengetahui cara mencari nilai numerik suatu polinomial sangat penting agar dapat menggunakan teorema sisa, sebuah teorema yang sangat penting tentang polinomial. Klik tautan ini dan cari tahu apa teorema sisanya , Anda akan menemukan penjelasannya, contoh penggunaan, dan latihan yang diselesaikan langkah demi langkah.
Contoh Nilai Numerik Polinomial
Agar Anda memahami cara mendapatkan nilai numerik polinomial, kami memberikan contoh penyelesaian lainnya:
Contoh 1
- Hitung nilai numerik polinomial
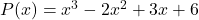
Untuk

![Rendered by QuickLaTeX.com \begin{aligned} P(-1) & =(-1)^3-2\cdot (-1)^2+3\cdot (-1)+6 \\[2ex] & = -1-2\cdot 1+3\cdot (-1)+6 \\[2ex] & =-1-2-3+6 \\[2ex]&= \bm{0} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3293713c5e12fac56d94be90f6bfc6e5_l3.png)
Dalam hal ini, nilai numerik polinomial sama dengan 0. Hal ini mempunyai konsekuensi karena sifat-sifat polinomial, karena berkat teorema faktor kita dapat mengetahui berapa sisa pembagian tertentu antar polinomial. Untuk mempelajari lebih lanjut, klik tautan sebelumnya, di mana kami menjelaskan apa teorema ini dan kegunaannya.
Contoh 2
- Tentukan nilai numerik polinomial
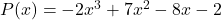
Untuk
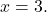
![Rendered by QuickLaTeX.com \begin{aligned} P(3) & =-2\cdot 3^3+7\cdot 3^2-8\cdot 3-2 \\[2ex] & =-2\cdot 27+7\cdot 9-8\cdot 3-2 \\[2ex] & =-54+63-24-2 \\[2ex]&= \bm{-17} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ad8b1145d569157b4e771adfae674e2c_l3.png)
Sejauh ini kita hanya melihat cara menentukan nilai numerik suatu polinomial dengan cara klasik, namun perlu Anda ketahui bahwa ada cara lain. Lebih khusus lagi, Anda juga dapat menghitung nilai numerik suatu polinomial dengan metode Ruffini . Anda juga harus mengetahui cara menggunakan prosedur ini, jadi kami sarankan untuk membaca penjelasan detailnya di tautan.
Nilai numerik polinomial dengan dua variabel atau lebih
Kita baru saja melihat cara mencari nilai numerik suatu polinomial jika polinomial tersebut hanya mempunyai satu variabel. Tapi… bagaimana cara mendapatkan nilai numerik suatu polinomial jika polinomial tersebut memiliki lebih dari satu variabel?
Nah, jika suatu polinomial memiliki 2 huruf atau lebih, maka nilai numeriknya harus dihitung dengan cara yang sama, yaitu ganti dulu setiap variabel dalam polinomial tersebut dengan nilai yang sesuai, lalu selesaikan operasi polinomialnya .
Sebagai contoh, Anda mempunyai masalah seperti ini yang diselesaikan di bawah ini:
- Temukan nilai numerik polinomial multivariat
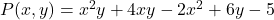
untuk nilai-nilai
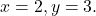
Pertama, kita ganti setiap variabel dengan nilainya yang sesuai, yaitu kita mengganti hurufnya
![]()
untuk 2 dan kami mengubah surat itu
![]()
oleh 3:
![]()
Kami memecahkan kekuatan:
![]()
Sekarang kita menghitung produknya:
![]()
Dan terakhir, kita melakukan penjumlahan dan pengurangan:
![]()
Jadi nilai numerik polinomial untuk data instruksi setara dengan 41.
Menyelesaikan latihan tentang nilai numerik polinomial
Latihan 1
Berapa nilai numerik polinomial P(x) untuk x=-2?
![]()
Untuk mencari nilai numerik polinomial, kita hanya perlu mensubstitusikan nilai yang diberikan dalam pernyataan ke dalam ekspresi polinomial dan menyelesaikan operasi yang dihasilkan:
![Rendered by QuickLaTeX.com \begin{aligned} P(-2) & =-2\cdot (-2)^3-4\cdot (-2)^2+3\cdot (-2)+8 \\[2ex] & =-2\cdot (-8)-4\cdot 4+3\cdot (-2)+8 \\[2ex] & =+16-16-6+8 \\[2ex]&= \bm{2} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-93b7cf1a6c7e930a0a70fc8302f4012d_l3.png)
Latihan 2
Hitung nilai numerik polinomial berikut dengan pecahan untuk x=4.
![]()
Baik polinomial tersebut memiliki pecahan atau tidak, prosedur untuk mencari nilai numerik polinomial tersebut selalu sama. Oleh karena itu kita harus mengganti variabel x dengan 4 dan menyelesaikan perhitungannya:
![Rendered by QuickLaTeX.com \begin{aligned} P(4) & =\cfrac{1}{2} \cdot 4^2-\cfrac{5}{4}\cdot 4+ 7 \\[2ex] & =\cfrac{1}{2} \cdot 16-\cfrac{5}{4}\cdot 4+ 7\\[2ex] & =8-5+7 \\[2ex]&= \bm{10} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-04fa4389b5e7c5257937ad35aed07c7b_l3.png)
Latihan 3
Tentukan nilai numerik polinomial untuk nilai x=3, y=5 dan z=-2
![]()
Untuk menentukan nilai numerik polinomial multivariat, cukup dengan mengganti nilai yang diberikan dalam soal ke dalam ekspresi aljabar dan menyelesaikan operasi yang dihasilkan:
![Rendered by QuickLaTeX.com \begin{aligned} P(3,5,-2) & =3^2\cdot 5\cdot (-2)+4\cdot 5^2\cdot (-2)^2-3\cdot 3^2\cdot (-2)+6\cdot 3\cdot 5 \cdot (-2) \\[2ex] & =9\cdot 5\cdot (-2)+4\cdot 25\cdot 4-3\cdot 9\cdot (-2)+6\cdot 3\cdot 5 \cdot (-2) \\[2ex] & =-90+400+54-180\\[2ex]&= \bm{184} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-29683a91c14427a8ea42c3518e59e53f_l3.png)
Latihan 4
Mengingat polinomial
![]()
menghitung nilai parameter
![]()
sehingga
![]()
Dalam soal ini, untuk mencari nilai yang tidak diketahui
![]()
kita perlu menyelesaikan persamaan tersebut
![]()
![]()
Oleh karena itu, kita coba hitung dulu nilai P(-2):
![Rendered by QuickLaTeX.com \begin{aligned} P(-2) & =-2\cdot (-2)^3-3\cdot (-2)^2+5\cdot (-2)+k \\[2ex] & =-2\cdot (-8)-3\cdot 4+5\cdot (-2)+k \\[2ex] & =+16-12-10+k\\[2ex]&=-6+k \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3b58398099c8033b93a559e2f0c87f1a_l3.png)
Sekarang kita menyamakan ekspresi yang diperoleh dengan 5:
![]()
![]()
Dan akhirnya, kita selesaikan persamaan yang dihasilkan:
![]()
![]()