Cara menghitung modulus suatu vektor

Pada halaman ini Anda akan melihat penjelasan tentang besaran suatu vektor dan cara menghitungnya beserta rumusnya. Anda juga akan dapat melihat cara mencari modul dari dua titik: asal dan akhir. Selain itu, Anda akan menemukan cara menentukan komponen suatu vektor dari modulusnya dan sifat-sifat modulus suatu vektor. Anda bahkan dapat berlatih dengan contoh, latihan, dan soal langkah demi langkah.

Berapakah modulus suatu vektor?

Besarnya suatu vektor menyatakan jarak antara titik asal dan titik akhir. Oleh karena itu, besar suatu vektor sama dengan panjang vektor tersebut.

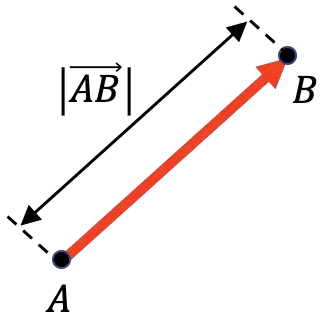
Seperti yang dapat Anda lihat pada representasi grafis di atas, besaran suatu vektor dilambangkan dengan garis vertikal di setiap sisi vektor:

$\lvert \vv{AB}\rvert$

Di sisi lain, modulus suatu vektor sama dengan norma suatu vektor , sehingga Anda dapat melihatnya ditulis seperti itu juga. Inilah sebabnya ada ahli matematika yang juga merepresentasikan modul vektor dengan dua garis vertikal di setiap sisinya:

$\lvert \lvert \vv{AB}\rvert\rvert$

Rumus modulus suatu vektor

Untuk mencari besar suatu vektor pada bidang, kita harus menerapkan rumus berikut:

Untuk menentukan besar suatu vektor, kita harus menghitung akar kuadrat (positif) dari jumlah kuadrat komponen-komponennya. Dengan kata lain, jika kita mempunyai vektor berikut:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

Modulnya adalah:

$\displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2}$

Misalnya kita akan menghitung besar vektor berikut dengan menggunakan rumus:

$\vv{\text{u}} = (4,3)$

$\lvert \vv{\text{u}} \rvert =\sqrt{4^2+3^2} = \sqrt{16+9}=\sqrt{25} = \bm{5}$

Hitung besarnya suatu vektor dengan koordinat asal dan ujungnya

Kita baru saja melihat bagaimana besaran suatu vektor ditentukan jika kita mengetahui komponen-komponennya, tetapi apa jadinya jika kita hanya mengetahui titik awal dan akhir vektor?

Jadi, untuk menghitung besaran suatu vektor dari koordinat asal dan akhirnya, Anda harus mengikuti dua langkah berikut:

Pertama kita cari komponen vektornya. Untuk melakukan ini, kita perlu mengurangkan titik ekstrem dikurangi titik asal.
Dan kemudian kita menghitung modulus vektor yang diperoleh dengan rumus yang kita lihat di bagian sebelumnya.

Mari kita lihat bagaimana hal ini dilakukan melalui sebuah contoh:

Hitunglah besar vektor yang titik asalnya adalah
$A(2,1)$

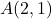
dan sebagai poin terakhir

$B(-1,4).$

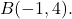
Pertama-tama kita perlu mencari komponen-komponen vektor, jadi kita kurangi titik akhirnya dikurangi titik asal:

$\vv{AB}=B-A=(-1,4)-(2,1)=(-3,3)$

Setelah kita mengetahui vektornya, kita menghitung besarnya menggunakan rumus besaran vektor:

$\begin{vmatrix} \vv{AB} \end{vmatrix} =\sqrt{(-3)^2+3^2} = \sqrt{9+9}=\sqrt{18}$

Dan kita biarkan hasilnya sebagai akar kuadrat, karena tidak eksak.

Cara menghitung komponen suatu vektor dari modulusnya

Kita telah melihat cara mengekstrak besaran suatu vektor dari komponen-komponennya, namun prosesnya juga dapat dibalik. Dengan kata lain, kita dapat menghitung komponen suatu vektor melalui modulusnya.

Proses mencari komponen suatu vektor dari besarnya disebut penguraian vektor . Jadi, untuk menguraikan suatu vektor tentu saja kita membutuhkan besarnya dan sudut yang dibentuknya terhadap sumbu absis (sumbu X).

Sehingga komponen X dan Y vektor dapat dihitung dengan perbandingan trigonometri:

Seperti terlihat pada gambar, besaran suatu vektor membentuk segitiga siku-siku dengan komponen-komponennya, sehingga rumus dasar trigonometri dapat diterapkan.

Harus diingat bahwa, tidak seperti modulus suatu vektor, komponen-komponennya dapat bernilai negatif karena sinus dan kosinus dapat bernilai negatif.

Sebagai contoh, kita akan menyelesaikan dekomposisi vektor dari vektor yang besar dan sudutnya terhadap sumbu OX adalah:

$\lvert \vv{\text{u}} \rvert = 10 \qquad \alpha = 60º$

Komponen horizontal suatu vektor sama dengan modulus dikalikan dengan kosinus sudut:

$\text{u}_x= \lvert \vv{\text{u}}\rvert \cdot \text{cos}(60º)= 10 \cdot 0,5 = 5$

Dan komponen vertikal vektor sama dengan mengalikan modulus dengan sinus sudut:

$\text{u}_y= \lvert \vv{\text{u}}\rvert \cdot \text{sen}(60º)= 10 \cdot 0,87 = 8,7$

Jadi vektornya adalah sebagai berikut:

$\vv{\mathbf{u}}\bm{ = (5 \ ,\ 8,7)}$

Sifat modulus suatu vektor

Modulus merupakan salah satu jenis operasi vektor yang mempunyai ciri-ciri sebagai berikut:

Besaran suatu vektor tidak pernah negatif , selalu sama dengan atau lebih besar dari 0.

$\lvert \vv{\text{u}} \rvert \geq 0$

Faktanya, satu-satunya vektor yang ada dengan besaran nol adalah vektor nol, yaitu vektor

$\vv{\text{u}}= (0,0) .$

Besaran hasil kali suatu vektor dengan bilangan real (atau skalar) sama dengan mengalikan nilai absolut skalar dengan besaran vektor. Oleh karena itu, persamaan berikut berlaku:

$\lvert k \cdot \vv{\text{u}} \rvert = \lvert k \rvert \cdot \lvert \vv{\text{u}} \rvert$

Pertidaksamaan segitiga diverifikasi: modulus jumlah dua vektor lebih kecil atau sama dengan jumlah modulusnya secara terpisah.

$\lvert \vv{\text{u}}+\vv{\text{v}} \rvert \leq \lvert\vv{\text{u}} \rvert+\lvert\vv{\text{v}} \rvert$

Selain itu, besaran jumlah dua vektor dihubungkan dengan perkalian titik dengan persamaan berikut:

$\lvert \vv{\text{u}}+\vv{\text{v}} \rvert = \sqrt{\lvert \vv{\text{u}} \rvert ^2+\lvert \vv{\text{v}} \rvert ^2 +2\cdot \vv{\text{u}}\cdot \vv{\text{v}} \vphantom{\sqrt{x^2}}}$

vektor satuan

Dalam matematika, vektor satuan adalah vektor yang modulusnya sama dengan satu.

$\lvert \vv{\text{u}} \rvert=1$

Oleh karena itu, panjang suatu vektor satuan adalah satu satuan.

Tampaknya sangat sulit bagi sebuah vektor untuk memiliki modulus tepat 1, namun sebenarnya mudah untuk menemukan jenis vektor ini:

Untuk mencari vektor satuan suatu vektor, cukup membaginya dengan modulusnya:

$\vv{\text{v}}_u = \cfrac{\vv{\text{v}}}{\lvert \vv{\text{v}} \rvert}$

Emas

$\vv{\text{v}}_u$

adalah vektor satuan dari

$\vv{\text{v}},$

Dan

$\lvert \vv{\text{v}} \rvert$

modul Anda.

Vektor satuan disebut juga versor atau vektor ternormalisasi.

Selain itu, vektor satuan mempunyai arah dan arah yang sama dengan vektor aslinya.

Misalnya, kita akan menghitung vektor satuan dari vektor berikut:

$\vv{\text{v}}=(1,-1)$

Untuk menormalkan vektor, pertama-tama kita perlu menghitung besarnya:

$\lvert \vv{\text{v}} \rvert=\sqrt{1^2+(-1)^2} = \sqrt{2}$

Dan terakhir, kita menghitung vektor satuan dengan membagi vektor asli dengan modulusnya:

$\displaystyle \vv{\text{v}}_u = \cfrac{\vv{\text{v}}}{\lvert \vv{\text{v}} \rvert} = \frac{(1,-1)}{\sqrt{2}}= \bm{\left(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}} \right)}$

Latihan modul vektor terpecahkan

Latihan 1

Hitung besarnya vektor berikut:

$\vv{a}=(6,8)$

lihat solusi

Untuk menghitung modul vektor kita harus menerapkan rumusnya:

$\lvert\vv{a} \rvert= \sqrt{6^2+8^2} =\sqrt{36+64} = \sqrt{100} = \bm{10}$

Latihan 2

Urutkan vektor-vektor berikut dari yang terpendek hingga terpanjang.

$\vv{a}=(4,-2)$

$\vv{b}=(3,1)$

$\vv{c}=(5,12)$

$\vv{d}=(-6,-3)$

lihat solusi

Panjang suatu vektor sama dengan besarnya. Oleh karena itu, kita perlu menghitung modulus semua vektor:

$\left|\vv{a}\right|= \sqrt{4^2+(-2)^2} =\sqrt{16+4} = \sqrt{20}$

$|\vv{b}|= \sqrt{3^2+1^2} =\sqrt{9+1} = \sqrt{10}$

$\begin{vmatrix}\vv{c}\end{vmatrix}= \sqrt{5^2+12^2} =\sqrt{25+144} = \sqrt{169} = 13$

$|\vv{d}| = \sqrt{(-6)^2+(-3)^2} =\sqrt{36+9} = \sqrt{45}$

Jadi, vektor-vektor yang diurutkan dari panjang (atau modul) terkecil hingga terbesar adalah:

$|\vv{b}|< \begin{vmatrix}\vv{a}\end{vmatrix} < |\vv{d}| < \begin{vmatrix}\vv{c}\end{vmatrix}$

Latihan 3

Tentukan besar vektor yang titik asalnya adalah

$A(-3,2)$

dan sebagai poin terakhir

$B(7,-4).$

lihat solusi

Untuk menghitung modulnya, Anda harus mencari vektornya terlebih dahulu. Untuk melakukan ini, kita kurangi titik ekstrem dikurangi titik asal:

$\vv{AB}=B-A=(7,-4)-(-3,2)=(10,-6)$

Setelah kita mengetahui vektornya, modulusnya dihitung menggunakan rumus modulus:

$\begin{vmatrix} \vv{AB} \end{vmatrix} =\sqrt{10^2+(-6)^2} = \sqrt{100+36}=\bm{\sqrt{136}}$

Latihan 4

Uraikan vektor berikut dan temukan komponen-komponennya:

$\lvert \vv{a} \rvert =8 \qquad \alpha = 45º$

lihat solusi

Komponen horizontal suatu vektor sama dengan modulus dikalikan dengan kosinus sudut:

$a_x= \lvert \vv{a}\rvert \cdot \text{cos}(45º)= 8 \cdot 0,71 = 5,66$

Dan komponen vertikal vektor sama dengan mengalikan modulus dengan sinus sudut:

$a_y= \lvert \vv{a}\rvert \cdot \text{sen}(45º)= 8 \cdot 0,71 = 5,66$

Jadi vektornya adalah sebagai berikut:

$\vv{\mathbf{u}}\bm{ = (5,66 \ ,\ 5,66)}$

Dalam hal ini kedua komponennya identik, yaitu sudut kemiringan vektor adalah 45º.

Latihan 5

Hitunglah vektor yang mempunyai arah dan arah yang sama dengan vektor berikut tetapi dengan modul 1.

$\vv{a} = (-4,3)$

lihat solusi

Vektor yang mempunyai arah dan arah yang sama tetapi dengan modul 1 adalah vektor satuan. Untuk menghitungnya, pertama-tama kita cari modul vektornya:

$\lvert \vv{a} \rvert=\sqrt{(-4)^2+3^2} = \sqrt{16+9} = \sqrt{25} = 5$