Metode Gaussian – Yordania -

Di halaman ini Anda akan mempelajari apa itu metode Gauss-Jordan dan cara menyelesaikan sistem persamaan menggunakan metode Gauss. Selain itu, Anda juga akan menemukan contoh dan penyelesaian latihan sistem dengan metode Gauss sehingga Anda dapat mempraktikkan dan memahaminya dengan sempurna.

Apa metode Gauss?

Metode Gauss-Jordan adalah prosedur yang digunakan untuk menyelesaikan sistem persamaan dengan 3 hal yang tidak diketahui, yaitu seperti ini:

$\left. \begin{array}{r} 3x-4y+5z=10 \\[2ex] x+5y-2z=4 \\[2ex] -x+4y+2z=-1 \end{array} \right\}$

Tujuan dari metode Gauss adalah untuk mengubah sistem persamaan awal menjadi sistem bertahap , yaitu sistem yang setiap persamaannya memiliki satu persamaan yang kurang diketahui dibandingkan persamaan sebelumnya:

$\left. \begin{array}{r} a_1x+b_1y+c_1z=d_1 \\[2ex] a_2x+b_2y+c_2z=d_2 \\[2ex] a_3x+b_3y+c_3z=d_3 \end{array} \right\} \ \bm{\longrightarrow} \left. \begin{array}{r} A_1x+B_1y+C_1z=D_1 \\[2ex] B_2y+C_2z=D_2 \\[2ex] C_3z=D_3 \end{array} \right\}$

Namun, untuk melakukannya, Anda harus terlebih dahulu mengetahui cara menyatakan sistem persamaan dalam bentuk matriks dan transformasi yang diperbolehkan pada matriks tersebut. Jadi kita akan menjelaskan kedua hal ini sebelumnya, dan kemudian kita akan melihat bagaimana prosedur menggunakan metode Gauss .

Matriks yang diperluas sistem

Sebelum melihat bagaimana sistem diselesaikan, Anda harus mengetahui bahwa sistem persamaan dapat dinyatakan dalam bentuk matriks: koefisien dari

$x}$

dimasukkan ke dalam kolom pertama, koefisien dari

$y}$

di kolom kedua, koefisien dari

$z$

di kolom ketiga dan angka tanpa diketahui di kolom keempat.

Misalnya:

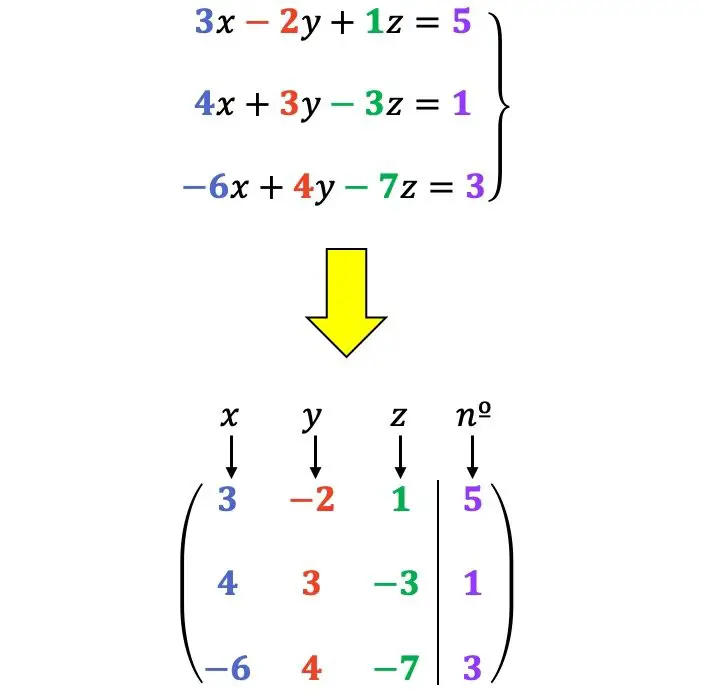
Transformasi baris diperbolehkan

Untuk mengubah sistem persamaan menjadi sistem berskala, salah satu operasi berikut dapat dilakukan pada matriks yang terkait dengan sistem:

Mengubah urutan baris dalam matriks.

Misalnya, kita dapat mengubah urutan baris 2 dan 3 suatu matriks:

$\left( \begin{array}{ccc|c} 3 & 5 & -2 & 1 \\[2ex] -2 & 4 & -1 & 2 \\[2ex] 6 & 1 & -3 & 10 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{ f_2 \rightarrow f_3}} \\[2ex] \xrightarrow{ f_3 \rightarrow f_2}} \end{array} \left( \begin{array}{ccc|c} 3 & 5 & -2 & 1 \\[2ex] 6 & 1 & -3 & 10 \\[2ex] -2 & 4 & -1 & 2 \end{array} \right)$

Kalikan atau bagi semua suku dalam satu baris dengan angka selain 0.

Misalnya, kita mengalikan baris 1 dengan 4 dan membagi baris 3 dengan 2:

$\left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 3 & -1 & 5 & -3 \\[2ex] 2 & -4 & -2 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{4 f_1} \\[2ex] \\[2ex] \xrightarrow{ f_3 / 2} \end{array} \left( \begin{array}{ccc|c} 4 & -8 & 12 & 4 \\[2ex] 3 & -1 & 5 & -3 \\[2ex] 1 & -2 & -1 & 3 \end{array} \right)$

Ganti sebuah baris dengan jumlah baris yang sama ditambah baris lainnya dikalikan dengan sebuah angka.

Misalnya, pada matriks berikut, kita menambahkan baris 2 ke baris 3 dikalikan 1:

$\left( \begin{array}{ccc|c} -1 & -3 & 4 & 1 \\[2ex] 2 & 4 & 1 & -5 \\[2ex] 1 & -2 & 3 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 1 \cdot f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} -1 & -3 & 4 & 1 \\[2ex] 3 & 2 & 4 & -6 \\[2ex] 1 & -2 & 3 & -1 \end{array} \right)$

Bagaimana cara menyelesaikan sistem persamaan menggunakan metode Gauss?

Sekarang kita akan melihat melalui contoh prosedur penyelesaian sistem persamaan dengan metode Gauss:

$\left. \begin{array}{r} -x+2y+2z=-24 \\[2ex] x+y+z=48 \\[2ex] 2x-6y+4z=12 \end{array} \right\}$

Hal pertama yang harus dilakukan adalah matriks yang diperluas dari sistem :

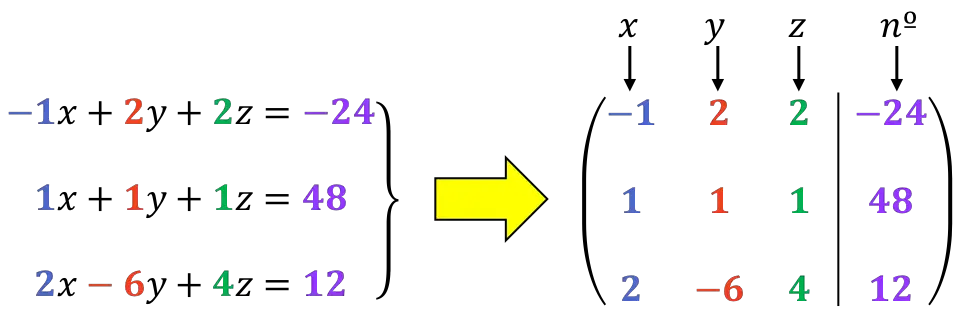
Contoh sistem persamaan yang diselesaikan dengan metode Gauss

Seperti yang akan kita lihat nanti, sebaiknya digit pertama pada baris pertama adalah 1. Oleh karena itu, kita akan mengubah urutan baris 1 dan 2:

$\left( \begin{array}{ccc|c} -1 & 2 & 2 &-24 \\[2ex] 1 & 1 & 1 & 48 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \xrightarrow{ f_1 \rightarrow f_2} \\[2ex] \xrightarrow{ f_2 \rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} \color{blue}\boxed{\color{black}1} & 1 & 1 & 48 \\[2ex] -1 & 2 & 2 &-24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right)$

Tujuan metode Gauss adalah membuat bilangan di bawah diagonal utama menjadi 0 . Artinya, kita perlu mengubah angka merah menjadi 0:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] \color{red}\bm{-1} & 2 & 2 &-24 \\[2ex] \color{red}\bm{2} & \color{red}\bm{-6} & 4 & 12 \end{array} \right)$

Untuk menghilangkan angka-angka ini, kita perlu melakukan transformasi baris yang sesuai.

Misalnya, -1 yang merupakan elemen pertama baris kedua adalah negatif dari 1, elemen pertama baris pertama. Oleh karena itu, jika kita menambahkan baris pertama ke baris kedua, -1 akan dihilangkan:

$\begin{array}{lccc|c} & -1 & 2 & 2 & -24 \\ + & \phantom{-}1 & 1 & 1 & \phantom{-}48 \\ \hline & \phantom{-}0 & 3 & 3 & \phantom{-}24 \end{array} \begin{array}{l} \color{blue}\bm{\leftarrow f_2} \\ \color{blue}\bm{\leftarrow f_1} \\ \phantom{hline} \\ \end{array}$

Jadi jika kita melakukan penjumlahan ini, kita akan mendapatkan matriks berikut:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] -1 & 2 & 2 & -24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] \color{blue}\boxed{\color{black}0} & 3 & 3 & 24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right)$

Dengan cara ini kami berhasil mengubah -1 menjadi 0.

Sekarang kita akan mentransformasikan 2. Jika Anda perhatikan, 2, yang merupakan elemen pertama pada baris ketiga, adalah dua kali lipat dari 1, elemen pertama pada baris pertama. Oleh karena itu, jika kita menambahkan baris pertama dikalikan -2 ke baris ketiga, maka angka 2 akan dihilangkan:

$\begin{array}{lccc|c} & \phantom{-}2 & -6 & \phantom{-}4 & \phantom{-}12 \\ + & -2 & -2 & -2 & -96 \\ \hline & \phantom{-}0 & -8 & \phantom{-}2 & -84 \end{array} \begin{array}{l} \color{blue} \bm{\leftarrow f_3} \\ \color{blue} \bm{\leftarrow -2 f_1} \\ \phantom{hline} \\ \end{array}$

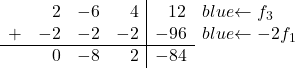
Oleh karena itu, kami mendapatkan matriks berikut:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-2f_1} \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] \color{blue}\boxed{\color{black}0} & -8 & 2 & -84 \end{array} \right)$

Dengan cara ini kami berhasil mengubah angka 2 menjadi 0.

Yang harus kita lakukan sekarang adalah mengubah -8 menjadi 0. Caranya, kita kalikan baris ketiga dengan 3 dan tambahkan baris kedua dikalikan 8:

$\begin{array}{lccc|r} & 0 & -24 & \phantom{2}6 & -252 \\ + & 0 & \phantom{-}24 & 24 & \phantom{-}192 \\ \hline & 0 & \phantom{-2}0 & 30 & -60 \end{array} \begin{array}{l}\color{blue}\bm{ \leftarrow 3f_3} \\\color{blue}\bm{ \leftarrow 8f_2} \\ \phantom{hline} \\ \end{array}$

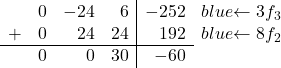
Oleh karena itu kami memperoleh matriks berikut:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & -8 & 2 & -84 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3f_3 + 8f_2} \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & \color{blue}\boxed{\color{black}0} & 30 & -60 \end{array} \right)$

Dan dengan transformasi ini, kita mendapatkan semua bilangan di bawah diagonal utama menjadi 0. Jadi sekarang kita bisa menyelesaikan sistem persamaannya.

Sekarang kita harus mengubah matriks tersebut menjadi sistem persamaan yang tidak diketahui . Untuk melakukan ini, ingatlah bahwa kolom pertama berhubungan dengan

$x$

, kolom kedua dari

$y$

, kolom ketiga dari

$z$

dan kolom terakhir adalah angka-angka yang tidak diketahui:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & 0 & 30 & -60 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x+1y+1z=48 \\[2ex] 3y+3z=24 \\[2ex] 30z=-60 \end{array} \right\}$

Dan terakhir, untuk menyelesaikan sistem ini, kita perlu menyelesaikan persamaan yang tidak diketahui dari bawah ke atas. Karena persamaan terakhir hanya mempunyai satu hal yang tidak diketahui, kita dapat menyelesaikannya dan mencari nilainya:

$30z=-60$

$z = \cfrac{-60}{30}$

$\bm{z=-2}$

Sekarang kita sudah mengetahui apa itu z, jika kita substitusikan nilainya ke dalam persamaan kedua, kita dapat mencari nilai dari

$y$

$3y+3z=24 \ \xrightarrow{z \ = \ -2} \ 3y+3(-2)=24$

$3y-6=24$

$3y=24+6$

$3y=30$

$y=\cfrac{30}{3}$

$\bm{y=10}$

Dan kita melakukan hal yang sama dengan persamaan pertama: kita mengganti nilai-nilai yang tidak diketahui lainnya dan menghapusnya

$x$

$1x+1y+1z=48 \ \xrightarrow{y \ = \ 10 \ ; \ z \ = \ -2} \ 1x+1(10)+1(-2)=48$

$x+10-2=48$

$x=48-10+2$

$\bm{x=40}$

Oleh karena itu, penyelesaian sistem persamaan tersebut adalah:

$\bm{x=40} \quad \bm{y=10} \quad \bm{z=-2}$

Menyelesaikan masalah sistem persamaan dengan metode Gauss-Jordan

Latihan 1

Selesaikan sistem persamaan berikut dengan menggunakan metode Gauss:

$\left. \begin{array}{r} x+y-z=2 \\[2ex] x-2y+3z=0 \\[2ex] 2x-y+3z=3 \end{array} \right\}$

lihat solusi

Hal pertama yang perlu kita lakukan adalah matriks yang diperluas dari sistem:

$\left. \begin{array}{r} x+y-z=2 \\[2ex] x-2y+3z=0 \\[2ex] 2x-y+3z=3 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 1 & -2 & 3 & 0 \\[2ex] 2 & -1 & 3 & 3 \end{array} \right)$

Sekarang kita perlu membuat semua angka di bawah array utama menjadi 0.

Oleh karena itu kami melakukan operasi baris untuk membatalkan dua suku terakhir dari kolom pertama:

$\left( \begin{array}{ccc|c}1 & 1 & -1 & 2 \\[2ex] 1 & -2 & 3 & 0 \\[2ex] 2 & -1 & 3 & 3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -f_1} \\[2ex] \xrightarrow{f_3-2f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & -3 & 5 & -1 \end{array} \right)$

Sekarang kita menghapus elemen terakhir dari kolom kedua:

$\left( \begin{array}{ccc|c}1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & -3 & 5 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & 0 & 1 & 1 \end{array} \right)$

Setelah semua bilangan di bawah diagonal utama adalah 0, sekarang kita dapat menyelesaikan sistem persamaannya. Untuk melakukan ini, kita nyatakan kembali matriks tersebut dalam bentuk sistem persamaan dengan yang tidak diketahui:

$\left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & 0 & 1 & 1 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+y-z=2 \\[2ex] -3y+4z=-2 \\[2ex] 1z=1 \end{array} \right\}$

Dan kami memecahkan persamaan yang tidak diketahui dari bawah ke atas. Pertama-tama kita selesaikan persamaan terakhir:

$1z= 1$

$z=\bm{1}$

Sekarang kita substitusikan nilai z ke dalam persamaan kedua untuk mencari nilai y:

$-3y+4z=-2 \ \xrightarrow{z \ = \ 1} \ -3y+4(1)=-2$

$-3y+4=-2$

$-3y=-2-4$

$-3y=-6$

$y=\cfrac{-6}{-3} = \bm{2}$

Dan kita melakukan hal yang sama dengan persamaan pertama: kita mengganti nilai-nilai yang tidak diketahui lainnya dan menyelesaikan x:

$x+y-z=2 \ \xrightarrow{y \ = \ 2 \ ; \ z \ = \ 1} \ x+(2)-(1)=2$

$x+1=2$

$x=2-1$

$\bm{x=1}$

Oleh karena itu, penyelesaian sistem persamaan tersebut adalah:

$\bm{x=1} \qquad \bm{y=2} \qquad \bm{z=1}$

Latihan 2

Temukan solusi sistem persamaan berikut dengan menggunakan metode Gauss:

$\left. \begin{array}{r} 2x+y+2z=-3 \\[2ex] x+3y+2z=5 \\[2ex] 4x+2y-z=-1 \end{array} \right\}$

lihat solusi

Hal pertama yang perlu kita lakukan adalah matriks yang diperluas dari sistem:

$\left. \begin{array}{r} 2x+y+2z=-3 \\[2ex] x+3y+2z=5 \\[2ex] 4x+2y-z=-1 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & 1 & 2 & -3 \\[2ex] 1 & 3 & 2 & 5 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right)$

Untuk menerapkan metode Gauss, akan lebih mudah jika bilangan pertama pada baris pertama adalah 1. Oleh karena itu, kita akan mengubah urutan baris 1 dan 2:

$\left( \begin{array}{ccc|c}2 & 1 & 2 & -3 \\[2ex] 1 & 3 & 2 & 5 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1\rightarrow f_2} \\[2ex] \xrightarrow{f_2\rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c}1 & 3 & 2 & 5 \\[2ex] 2 & 1 & 2 & -3 \\[2ex] 4 & 2 & -1 & -1\end{array} \right)$

Sekarang kita perlu membuat semua angka di bawah array utama menjadi 0.

Jadi kita melakukan operasi baris untuk mengganti dua elemen terakhir dari kolom pertama:

$\left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 2 & 1 & 2 & -3 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -2f_1} \\[2ex] \xrightarrow{f_3-4f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & -10 & -9 & -21 \end{array} \right)$

Sekarang kita mengubah elemen terakhir kolom kedua menjadi nol:

$\left( \begin{array}{ccc|c}1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & -10 & -9 & -21\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-2f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & 0 & -5 & 5 \end{array} \right)$

Setelah semua bilangan di bawah diagonal utama adalah 0, kita dapat menyelesaikan sistem persamaannya. Untuk melakukan ini, kita nyatakan kembali matriks tersebut dalam bentuk sistem persamaan dengan yang tidak diketahui:

$\left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & 0 & -5 & 5 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+3y+2z=5 \\[2ex] -5y-2z=-13 \\[2ex] -5z=5 \end{array} \right\}$

Dan kami memecahkan persamaan yang tidak diketahui dari bawah ke atas. Pertama-tama kita selesaikan persamaan terakhir:

$-5z= 5$

$z=\cfrac{5}{-5}=\bm{-1}$

Sekarang kita substitusikan nilai z ke dalam persamaan kedua untuk mencari nilai y:

$-5y-2z=-13 \ \xrightarrow{z \ = \ -1} \ -5y-2(-1)=-13$

$-5y+2=-13$

$-5y=-13-2$

$-5y=-15$

$y=\cfrac{-15}{-5} = \bm{3}$

Dan kita melakukan hal yang sama dengan persamaan pertama: kita mengganti nilai-nilai yang tidak diketahui lainnya dan menyelesaikan x:

$x+3y+2z=5 \ \xrightarrow{y \ = \ 3 \ ; \ z \ = \ -1} \ x+3(3)+2(-1)=5$

$x+9-2=5$

$x=5-9+2$

$\bm{x=-2}$

Oleh karena itu, penyelesaian sistem persamaan tersebut adalah:

$\bm{x=-2} \qquad \bm{y=3} \qquad \bm{z=-1}$

Latihan 3

Hitung penyelesaian sistem persamaan berikut dengan metode Gauss:

$\left. \begin{array}{r} 2x+3y+z=-1 \\[2ex] 6x+4y+4z=0 \\[2ex] -4x+2y-z=5 \end{array} \right\}$

lihat solusi

Hal pertama yang perlu kita lakukan adalah matriks yang diperluas dari sistem:

$\left. \begin{array}{r} 2x+3y+z=-1 \\[2ex] 6x+4y+4z=0 \\[2ex] -4x+2y-z=5\end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 6 & 4 & 4 & 0 \\[2ex] -4 & 2 & -1 & 5 \end{array} \right)$

Sekarang kita perlu membuat semua angka di bawah array induk menjadi 0.

Jadi kita melakukan operasi baris untuk mengganti dua elemen terakhir dari kolom pertama:

$\left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 6 & 4 & 4 & 0 \\[2ex] -4 & 2 & -1 & 5\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -3f_1} \\[2ex] \xrightarrow{f_3+2f_1} & \end{array} \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 8 & 1 & 3\end{array} \right)$

Sekarang kita mengubah elemen terakhir kolom kedua menjadi nol:

$\left( \begin{array}{ccc|c}2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 8 & 1 & 3\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5f_3+8f_2} & \end{array} \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 0 & 13 & 39 \end{array} \right)$

$\left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 0 & 13 & 39\end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 2x+3y+1z=-1 \\[2ex] -5y+z=3 \\[2ex] 13z=39 \end{array} \right\}$

Dan kami memecahkan persamaan yang tidak diketahui dari bawah ke atas. Pertama-tama kita selesaikan persamaan terakhir:

$13z= 39$

$z=\cfrac{39}{13}=\bm{3}$

Sekarang kita substitusikan nilai z ke dalam persamaan kedua untuk mencari nilai y:

$-5y+z=3 \ \xrightarrow{z \ = \ 3} \ -5y+(3)=3$

$-5y=3-3$

$-5y=0$

$y=\cfrac{0}{-5} = \bm{0}$

Dan kita melakukan hal yang sama dengan persamaan pertama: kita mengganti nilai-nilai yang tidak diketahui lainnya dan menyelesaikan x:

$2x+3y+1z=-1 \ \xrightarrow{y \ = \ 0 \ ; \ z \ = \ 3} \ 2x+3(0)+1(3)=-1$

$2x+0+3=-1$

$2x=-1-3$

$2x=-4$

$x=\cfrac{-4}{2}=\bm{-2}$

Oleh karena itu, penyelesaian sistem persamaan tersebut adalah:

$\bm{x=-2} \qquad \bm{y=0} \qquad \bm{z=3}$

Latihan 4

Selesaikan sistem persamaan berikut dengan 3 yang tidak diketahui menggunakan metode Gauss:

$\left. \begin{array}{r} 2x-6=4y+6z \\[2ex] -y-3z=1-3x \\[2ex] -4x-y=6-3z \end{array} \right\}$

lihat solusi

Sebelum menerapkan metode Gauss, kita perlu menyusun sistem persamaannya sehingga semua yang tidak diketahui berada di sebelah kiri persamaan dan angka-angkanya berada di sebelah kanan:

$\left. \begin{array}{r}2x-6=4y+6z \\[2ex] -y-3z=1-3x \\[2ex] -4x-y=6-3z \end{array} \right\} \longrightarrow \left. \begin{array}{r} 2x-4y-6z=6 \\[2ex] 3x-y-3z=1 \\[2ex] -4x-y+3z=6\end{array} \right\}$

Setelah sistem diurutkan, kami membangun matriks sistem yang dikembangkan:

$\left. \begin{array}{r} 2x-4y-6z=6 \\[2ex] 3x-y-3z=1 \\[2ex] -4x-y+3z=6 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & -4 & -6 & 6 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right)$

Karena semua bilangan pada baris pertama adalah bilangan genap, sebelum mengerjakan baris-baris tersebut kita akan membagi baris pertama dengan 2. Karena ini akan mempermudah penghitungan:

$\left( \begin{array}{ccc|c}2 & -4 & -6 & 6 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{f_1/2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6\end{array} \right)$

Sekarang kita perlu membuat semua angka di bawah array utama menjadi 0.

Jadi kita melakukan operasi baris untuk mengganti dua elemen terakhir dari kolom pertama:

$\left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -3f_1} \\[2ex] \xrightarrow{f_3+4f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -9 & -9 & 18\end{array} \right)$

Seperti sebelumnya, karena semua angka pada baris terakhir adalah kelipatan 9, maka kita akan membaginya dengan 9 agar perhitungannya lebih mudah:

$\left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -9 & -9 & 18 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex]\xrightarrow{f_3/9} & \end{array} \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -1 & -1 & 2\end{array} \right)$

Sekarang kita mengubah elemen terakhir kolom kedua menjadi nol:

$\left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -1 & -1 & 2\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5f_3+f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & 0 & 1 & 2 \end{array} \right)$

$\left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & 0 & 1 & 2 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x-2y-3z=3 \\[2ex] 5y+6z=-8 \\[2ex] 1z=2 \end{array} \right\}$