Di sini Anda akan menemukan cara menghitung titik potong (atau perpotongan) antara dua garis. Anda juga akan melihat contoh dan Anda dapat berlatih dengan latihan yang diselesaikan langkah demi langkah.
Berapakah titik potong atau perpotongan antara dua garis?
Titik potong (atau potong) antara dua garis adalah titik perpotongan dua garis yang berbeda. Oleh karena itu, apabila dua garis yang berbeda mempunyai perpotongan atau titik potong, berarti keduanya berhimpitan pada satu titik.
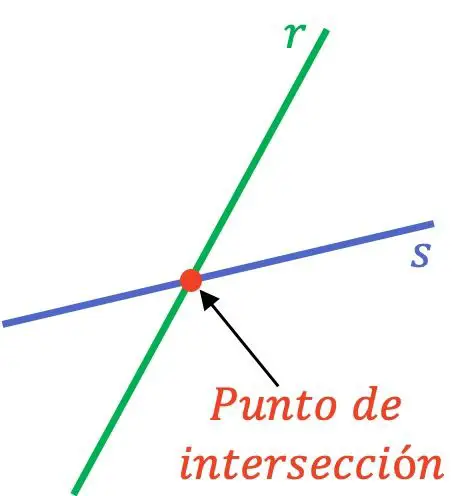
Agar dua garis berpotongan di suatu titik, kedua garis tersebut harus merupakan garis yang berpotongan, karena garis sejajar tidak bersentuhan di titik mana pun.
Jika Anda tidak ingat persis apa yang dimaksud dengan garis berpotongan, sebaiknya periksa halaman Contoh Garis Berpotongan , di mana Anda akan menemukan penjelasan mendetail tentang jenis garis tersebut dan cara mengetahui apakah dua garis berpotongan atau tidak.
Bagaimana cara menghitung titik potong atau perpotongan antara dua garis?
Setelah kita melihat pengertian titik potong atau perpotongan antara dua garis, sekarang mari kita lihat bagaimana cara menghitung titik tersebut.
Untuk mencari titik potong (atau perpotongan) antara dua garis, pertama-tama Anda harus memastikan bahwa kedua garis tersebut tidak sejajar, karena jika merupakan dua garis sejajar maka tidak akan berpotongan di titik mana pun. Oleh karena itu, Anda perlu mengetahui terlebih dahulu cara menentukan dua garis sejajar dan tidak; Jika Anda tidak ingat cara melakukannya, Anda dapat menontonnya lagi dengan mengklik link tersebut.
Setelah kita mengetahui bahwa kedua garis tersebut tidak sejajar, maka untuk menentukan titik potong (atau perpotongan) antara kedua garis tersebut, kita harus menyelesaikan sistem persamaan yang dibentuk oleh persamaan masing-masing garis. Dan hasil dari sistem persamaan tersebut adalah koordinat titik potong (atau perpotongan) antara kedua garis tersebut.
Contoh cara mencari titik potong atau perpotongan antara dua garis
Sebagai contoh, kita akan menyelesaikan suatu soal sehingga Anda dapat melihat cara mencari titik potong (atau perpotongan) antara 2 garis:
- Temukan titik potong antara dua garis berikut:
![]()
Pertama, garis-garis tersebut tidak sejajar karena mempunyai kemiringan yang berbeda, sehingga keduanya berpotongan di suatu titik pada bidang kartesius.
Untuk mengetahuinya, kita harus menyelesaikan sistem persamaan yang terdiri dari persamaan setiap garis:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} y=4x-1 \\[2ex] y=-2x+5 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9a1cdd55c61dc9a42ce97d3f66759831_l3.png)
Dalam kasus khusus ini, kita akan menyelesaikan sistem dengan metode pemerataan karena dua hal yang tidak diketahui
![]()
sudah terselesaikan (kedua baris berada dalam bentuk persamaan eksplisit):
![]()
![]()
Kami menghapus nilai variabel
![]()
![]()
![]()
![]()
![]()
Dan begitu Anda tahu berapa nilainya
![]()
Kami mengganti nilainya ke dalam persamaan apa pun untuk menemukan nilainya
![]()
![]()
![]()
![]()
Sehingga koordinat titik potong kedua garis tersebut adalah:
![]()
Menyelesaikan permasalahan titik potong atau perpotongan antara dua garis
Latihan 1
Berapakah titik potong atau perpotongan antara dua garis berikut?
![]()
Pertama, garis-garis tersebut tidak sejajar karena mempunyai kemiringan yang berbeda, sehingga kedua garis tersebut akan bertemu di suatu titik pada bidang tersebut.
Untuk menghitung titik tersebut, perlu diselesaikan sistem persamaan yang dibentuk oleh persamaan setiap garis:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} y=x+5 \\[2ex] y=2x+3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cb0689e91892970c4231287d01e21bce_l3.png)
Dalam hal ini, kita akan menyelesaikan sistem persamaan dengan metode pemerataan karena dua hal tidak diketahui
![]()
sudah terselesaikan (kedua baris berada dalam bentuk persamaan eksplisit):
![]()
![]()
Kami menghapus nilai variabel
![]()
![]()
![]()
![]()
Dan begitu Anda tahu berapa nilainya
![]()
Kami mengganti nilainya ke dalam persamaan apa pun untuk menemukan nilainya
![]()
![]()
![]()
Maka koordinat titik potong kedua garis tersebut adalah:
![]()
Latihan 2
Carilah titik potong atau perpotongan antara dua garis berikut:
![]()
hak
![]()
Dinyatakan dalam bentuk persamaan implisit (atau umum), maka kita lewati terlebih dahulu dalam bentuk persamaan eksplisit untuk mengetahui nilai kemiringannya:
![]()
![]()
![]()
![]()
Jadi kedua garis tersebut mempunyai kemiringan yang berbeda sehingga terdapat titik potong diantara keduanya.
Untuk menghitung titik tersebut, perlu diselesaikan sistem persamaan yang dibentuk oleh persamaan setiap garis:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} y=-3x+1\\[2ex] y=-2x-3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cc914ee4de930feec594f04f5867ba7d_l3.png)
Kami menyelesaikan sistem persamaan dengan metode pemerataan:
![]()
![]()
Kami menghapus nilai variabel
![]()
![]()
![]()
![]()
Dan begitu Anda tahu berapa nilainya
![]()
Kami mengganti nilainya ke persamaan mana pun untuk menemukan nilai
![]()
![]()
![]()
![]()
Maka koordinat titik potong kedua garis tersebut adalah:
![]()
Latihan 3
Tentukan titik potong atau perpotongan antara dua garis berikut:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=1+2t \\[1.7ex] y=-2-3t \end{cases} \qquad \qquad s: \ 4x+2y+8=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-4493e6356538f2224d935cdff1a5a0e7_l3.png)
Pertama-tama kita perlu mengetahui apakah kedua garis tersebut sejajar atau tidak. Untuk melakukan ini, kita akan melihat apakah vektor arah kedua garis sebanding.
hak
![]()
didefinisikan dalam bentuk persamaan parametrik, sehingga komponen vektor arahnya adalah koefisien di depan parameter
![]()
![]()
Dan, di sisi lain, garisnya
![]()
digambarkan dalam bentuk persamaan implisit, sehingga vektor arahnya adalah:
![]()
Sehingga komponen-komponen vektor dua arah tersebut tidak sebanding satu sama lain, sehingga kedua garis tersebut tidak sejajar.
![]()
Dan karena kedua garis tersebut tidak sejajar, maka berarti memang ada titik potong di antara keduanya. Untuk menghitungnya, kita harus menyelesaikan sistem persamaan yang dibentuk oleh persamaan setiap garis:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=1+2t \\[1.7ex] y=-2-3t \end{cases} \qquad \qquad s: \ 4x+2y+8=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-4493e6356538f2224d935cdff1a5a0e7_l3.png)
Dalam hal ini, seperti garis
![]()
berbentuk persamaan parametrik, maka ekspresi setiap persamaan parametrik perlu disubstitusikan ke persamaan garis lainnya:
![]()
Sekarang mari kita selesaikan persamaan yang dihasilkan:
![]()
![]()
![]()
![]()
![]()
dan mengganti nilai
![]()
ditemukan dalam persamaan parametrik untuk mencari koordinat titik potong:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=1+2t \\[1.7ex] y=-2-3t \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fd959e49e9461d7dd34898128ee1d43e_l3.png)
![Rendered by QuickLaTeX.com \begin{cases} x=1+2(-4)=1-8=-7 \\[1.7ex] y=-2-3(-4)=-2+12=10\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6c298c87a64b01e8495d050d39d48b5b_l3.png)
Jadi titik potong kedua garis tersebut adalah:
![]()