Kelipatan persekutuan terkecil (KPK) dari dua bilangan atau lebih adalah kelipatan persekutuan terkecil (bukan nol) yang dimiliki bilangan-bilangan tersebut. Ini adalah operasi kebalikan dari pembagi persekutuan terbesar , meskipun dihitung menggunakan metode serupa. Jika Anda ingin mempelajari cara menghitung KPK, sebaiknya Anda terus membaca, karena pada artikel ini kami akan menjelaskan semua prosedur (dari yang paling sederhana hingga yang paling rumit) untuk mencari kelipatan persekutuan terkecil dari suatu himpunan bilangan.
kalkulator lcm
Sebelum kita mulai berbicara tentang cara mendapatkan lcm, kami ingin Anda tahu bahwa di halaman ini kami memiliki kalkulator kelipatan persekutuan terkecil . Dengannya Anda akan dapat menghitung lcm dari semua angka yang Anda inginkan, dengan cara ini Anda dapat membandingkan hasil latihan Anda untuk melihat apakah Anda telah menyelesaikannya dengan benar.
Bagaimana cara menghitung kelipatan persekutuan terkecil?
Untuk mencari kelipatan persekutuan terkecil dari dua bilangan atau lebih, Anda perlu mengikuti salah satu dari tiga cara yang akan kami jelaskan di bawah ini. Selanjutnya, ketika kami merinci setiap prosedur yang dapat Anda pilih, kami juga akan memberi tahu Anda apa kelebihan dan kekurangannya. Dengan cara ini Anda akan mengetahui mana yang harus dipilih dalam setiap situasi untuk menyelesaikan KPK yang dimaksud dengan mudah dan cepat.
Metode 1: Daftar Berganda
Cara pertama adalah dengan membuat daftar kelipatan bilangan yang ingin dihitung dalam KPK. Maka Anda perlu menemukan nilai terkecil yang berulang di semua daftar , dengan cara ini Anda akan mendapatkan kelipatan persekutuan terkecil. Kemudian kita akan melihatnya dengan contoh: lcm (5, 6).
Kelipatan 5: 5, 10, 15, 20, 25, 30 , 35, 40...
Kelipatan 6 : 6, 12, 18, 24, 30 , 36, 42, 48...
Kami mencari persamaan terkecil dan kami sudah memiliki lcmnya.
cm (5, 6) = 30
Metode 2: dekomposisi faktorial
Kedua, kita dapat memilih untuk memfaktorkan angka-angka tersebut. Lebih spesifiknya, cara ini akan memudahkan dalam menghitung pcm bilangan besar . Karena mengikuti metode 1 saat mengerjakan lcm bilangan besar bisa jadi lambat dan membosankan, hanya karena kita harus menulis daftar kelipatan yang sangat panjang. Prosedur kedua ini mungkin sedikit lebih rumit untuk dipahami pada awalnya, namun jika Anda memahami mekanismenya, ada banyak keunggulan dibandingkan prosedur sebelumnya. Karena itu, mari kita lihat prosedur yang harus diikuti:
- Dekomposisi faktorial: langkah pertama adalah menguraikan semua bilangan yang akan kita masukkan ke dalam KPK menjadi faktor prima. Jika Anda belum tahu cara menguraikan suatu bilangan secara faktorial , sebaiknya masuk ke tautan terakhir ini, di sana Anda akan menemukan penjelasan kelas satu tentang cara menyederhanakan bilangan dengan cepat dan efisien.
- Buatlah ekspresi matematika tunggal: Jika semua bilangan dinyatakan sebagai faktor prima, kita akan memilih bilangan persekutuan dan bilangan bukan persekutuan yang dipangkatkan ke eksponen terbesar. Kemudian Anda menuliskannya sebagai ekspresi matematika tunggal dan akhirnya Anda menyelesaikan perkalian dan/atau pangkat yang diperlukan. Dan Anda sudah memiliki nilai numerik lcm.
Metode 3: Rumus matematika
Ada cara terakhir untuk mendapatkan kelipatan persekutuan terkecil, yaitu dengan menggunakan GCD dan rumus matematika berikut:
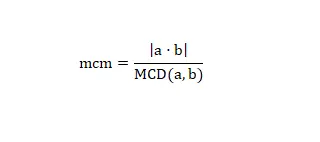
Dengan menggunakan rumus ini kita dapat menghitung lcm suatu bilangan. Mari kita lihat contoh nyata, jika kita ingin menghitung lcm (2,6) kita hanya perlu menyelesaikan operasi (2 x 6) / 2 = 6. Dan kita sudah menyelesaikan perhitungannya, seperti yang Anda lihat, ini adalah metode yang sederhana dan cepat jika Anda memiliki GCD atau dapat dengan mudah menghitungnya.
Tips menghitung lcm dengan cepat
Jika Anda sudah menguasai ketiga cara yang baru saja kami jelaskan, sebaiknya Anda membaca sifat-sifat kelipatan persekutuan terkecil yang akan kita bahas sekarang. Karena berkat mereka Anda akan dapat mengidentifikasi beberapa situasi spesifik di mana KPK dapat dihitung dengan sangat cepat, tanpa harus menggunakan strategi yang telah dijelaskan.
- Bilangan pertama habis dibagi bilangan kedua: jika kita ingin menghitung kelipatan persekutuan terkecil dari a dan b ketika a membagi b, maka ppcm kedua bilangan tersebut adalah yang terbesar (dalam hal ini b). Misal mau hitung KPK dari 2 dan 8 maka hasilnya paling besar, jadi 8.
- Dua bilangan prima: Dalam hal menemukan dua bilangan prima , cara tercepat adalah dengan mengalikannya dan hasilnya adalah ppcm. Hal ini logis, karena pembagi persekutuan terbesarnya adalah 1, yang berarti kita tidak akan dapat menguraikan bilangan tersebut menjadi faktor-faktor yang lebih sederhana daripada bilangan itu sendiri dan oleh karena itu, kita hanya dapat mengalikannya. Misalnya KPK dari 3 dan 5 adalah hasil perkaliannya: 3 x 5 = 15.
Bagaimana cara mendapatkan kelipatan persekutuan terkecil dalam pecahan?
Saat kita ingin menyelesaikan penjumlahan atau pengurangan pecahan, kita perlu menghitung penyebut persekutuan terkecil, yaitu sama dengan lcm, tetapi diterapkan pada pecahan. Pada dasarnya, kita mencari lcm dari kedua penyebutnya sehingga kita dapat menyatakan jumlahnya sebagai pecahan tunggal. Jika Anda ingin melihat bagaimana penyebut persekutuan terendah diterapkan pada penghitungan pecahan nyata, Anda dapat masuk ke tautan ini .
Lcm pada kalkulator ilmiah
Kunci KPK, yang terdapat pada kalkulator ilmiah apa pun, memungkinkan Anda menghitung kelipatan persekutuan terkecil dari dua bilangan bulat. Untuk kalkulator Casio, sintaks atau prosedur yang perlu Anda ikuti adalah sebagai berikut. Pertama kalian tekan APHA + MCM (tombol terakhir ini akan diberi label coklat). Setelah selesai, Anda dapat memasukkan kedua angka tersebut, namun perlu diingat bahwa Anda harus memisahkannya dengan koma ( SHIFT + , ). Terakhir, Anda akan mendapatkan kelipatan persekutuan terkecil dengan mengklik tombol sama dengan.
Latihan KPK diselesaikan langkah demi langkah
Selanjutnya, kami akan menunjukkan kepada Anda tiga contoh kelipatan persekutuan terkecil yang diselesaikan langkah demi langkah . Dengan cara ini Anda dapat mencoba memecahkan masalah tersebut dan mempraktikkan sedikit dari apa yang telah kami jelaskan di artikel ini. Penting bagi Anda untuk mencoba menyelesaikan latihan jika Anda ingin menginternalisasi konsep, karena teori perlu diterapkan pada kenyataan. Oleh karena itu, kami mengizinkan Anda berlatih dengan latihan:
Hitung KPK dari 4 dan 6
Kelipatan 4: 4, 8, 12 , 16, 20, 24 , 28, 32, 36 ...
Kelipatan 6: 6, 12 , 18, 24 , 30, 36 , 42, 48...
Kami akan menyelesaikan latihan ini menggunakan metode 1 (daftar kelipatan). Untuk memulai, kita perlu mengidentifikasi persamaan yang dimiliki kedua daftar tersebut dan kita akan memilih daftar yang lebih kecil. Jadi kelipatan persekutuan terkecil dari 4 dan 6 adalah 12 .
Hitung KPK dari 6 dan 9
Kelipatan 6: 6, 12, 18 , 24, 30, 36 , 42, 48...
Kelipatan 9: 9, 18 , 27, 36 , 45, 54, 63, 72...
Kita akan menyelesaikan latihan kedua ini dengan menggunakan metode yang sama seperti latihan sebelumnya. Untuk memulai, kita perlu mengidentifikasi yang paling umum dari dua daftar dan kita akan memilih yang kecil. Jadi kelipatan persekutuan terkecil dari 6 dan 9 adalah 18 .
Hitung KPK dari 30 dan 40
Faktorisasi prima 30 : 2 x 3 x 5
Faktorisasi prima dari 40: 2³ x 5
Kita akan menyelesaikan latihan terakhir ini dengan metode dekomposisi faktorial. Oleh karena itu, pertama-tama kita harus menyatakan kedua bilangan tersebut dalam faktor prima dan kita akan memilih bilangan persekutuan dan bilangan bukan persekutuan yang dipangkatkan terbesar. Jadi KPK dari 30 dan 40 adalah 2³ x 3 x 5 = 120.